|
| [56] m2mm | 2009-07-19 14:25:26 |
 Mármint
Tomon István 7 7 7 7 7 0 35 Gold medal
Szűcs Gergely 7 7 1 0 3 0 18 Bronze medal
Nagy János 7 7 7 2 7 0 30 Silver medal
Nagy Dániel 7 7 1 5 3 0 23 Bronze medal
Kornis Kristóf 7 7 0 2 7 0 23 Bronze medal
Éles András 7 7 2 5 7 0 28 Silver medal
|
| Előzmény: [55] m2mm, 2009-07-19 14:23:03 |
|
| [55] m2mm | 2009-07-19 14:23:03 |
 Gratulálok a magyar csapat tagjainak!
Az eredmények:
Tomon István 7 7 7 7 7 0 35 Gold medal
Szűcs Gergely 7 7 1 0 3 0 18 Bronze medal
Nagy János 7 7 7 27 0 30 Silver medal
Nagy Dániel 7 7 1 53 0 23 Bronze medal
Kornis Kristóf 7 7 0 27 0 23 Bronze medal
Éles András 7 7 2 57 0 28 Silver medal
|
|
| [54] Kós Géza | 2009-07-17 18:09:41 |
 Az idei feladatok
(Szabad fordításban)
I. nap
1. feladat. Legyen n pozitív egész, és legyenek a1,a2,a3,...,ak (k 2) különbző egészek az {1,2,...,n} halmazból úgy, hogy ai(ai+1-1) osztható n-nel minden egyes i=1,2,...,k-1 esetén. Bizonyítsuk be, hogy ak(a1-1) nem osztható n-nel. 2) különbző egészek az {1,2,...,n} halmazból úgy, hogy ai(ai+1-1) osztható n-nel minden egyes i=1,2,...,k-1 esetén. Bizonyítsuk be, hogy ak(a1-1) nem osztható n-nel.
2. feladat. Az ABC háromszög köré írt kör középpontja O. P és Q belső pontjai a CA, illetve AB oldalaknak. Legyen K, L és M a BP, CQ, illetve PQ szakaszok felezőpontja, és legyen  a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha  érinti a PQ egyenest, akkor OP=OQ. érinti a PQ egyenest, akkor OP=OQ.
3. feladat. Tegyük fel, hogy s1,s2,s3,... egy pozitív egészekből álló, szigorúan növekvő sorozat, amire az ss1,ss2,ss3,... és ss1+1,ss2+1,ss3+1,... részsorozatok számtani sorozatok. Bizonyítsuk be, hogy s1,s2,s3,... maga is számtani sorozat.
II. nap
4. feladat. Az ABC háromszögben AB=AC. A CAB és az ABC szög felezője a BC és CA olalakat D-ben, illetve E-ben metszi. Legyen K az ADC háromszögbe írt kör középpontja. Tegyük fel, hogy BEK =45o. Határozzuk meg a CAB szög összes lehetséges értékét. =45o. Határozzuk meg a CAB szög összes lehetséges értékét.
5. feladat. Határozzuk meg az összes olyan, a pozitív egészek halmazából a pozitív egészek halmazába képező f függvényt, amire tetszőleges a,b pozitív egészek esetén az a, f(b) és f(b+f(a)-1) hosszúságú szakaszokból (nem elfajuló) háromszög szerkeszthető.
6. feladat. Legyenek a1,a2,...,an különböző pozitív egészek, és legyen M egy n-1 pozitív egészből álló halmaz, ami nem tartalmazza az s=a1+a2+...+an számot. Egy szöcskének, a számegyenes 0 pontjából indulva, összesen n-szer kell ugrania jobb felé úgy, hogy az ugrások hossza rendre a1,a2,...,an legyen valamilyen sorrendben. Bizonyítsuk be, hogy az ugrások sorrendjét meg tudjuk választani úgy, hogy a szöcske egyszer se lépjen M-beli pontra.
|
|
| [53] lorantfy | 2008-07-24 19:56:22 |
 GRATULÁLOK A MAGYAR CSAPAT MINDEN TAGJÁNAK!
|
 |
|
| [52] Diego2 | 2008-07-21 18:53:57 |
 Nagyon nagy dolog, amit a fiúk műveltek. Ez nem vicc, gyerekek. Le a kalappal! Gratulálok az egész magyar csapatnak és mindenkinek, akinek ehhez a világraszóló sikerhez valamilyen köze van! Mert tetszik van nem, igenis, többek között az ilyen tudás az IGAZI ÉRTÉK! Nem lehet pénzben kifejezni.
|
|
|
| [50] Róbert Gida | 2008-07-20 18:38:52 |
 Eredmények:
http://www.imo-2008.es/results.html
Lovász fia negyedik lett az összes induló között, másodikban vesztett pontot.
Ezt a számolós második példának az a részét beadtam a Mathematica-nak, nem tudta bebizonyítani, tehát annyira mégsem könnyű, legalábbis egy gépnek. Csak a teljesen triviális jobboldal=0-át tudta belátni.
|
|
|
|
| [47] sakkmath | 2008-07-18 16:54:09 |
 Ha jó angolul is, klikk ide. Itt az "S"-ikonokra kattintva a megoldásokhoz jutunk. Magyarul két lehetőség adódik:
1) Egy könyv: Reiman István - Dobos Sándor: Nemzetközi Matematikai Diákolimpiák 1959 - 2003 (TypoTex, 2000, ISBN : 9639548045);
2) Egy lap: KöMaL 2000. év októberi száma. (Legalábbis ebben kell lennie, ugyanis az elmúlt évek gyakorlata ez: a szeptemberi számban a feladatokat és a beszámolót közlik, s a következőben hozzák a magyar olimpikonok megoldásait.
|
| Előzmény: [46] m2mm, 2008-07-18 12:58:42 |
|
| [46] m2mm | 2008-07-18 12:58:42 |
 Üdv! Valaki megtudná mondani, hol találhatom meg a 41. diákolimpia(2000 júliusa) feladatainak megoldását?
|
|
|
| [44] Róbert Gida | 2008-07-16 16:30:30 |
 2008-as spanyolországi matematikai olimpia első napjának feladatai:
1. Legyen H egy ABC hegyesszögű háromszög magasságpontja.  A kör középpontja a BC oldalfelezőpontja, és átmegy H-n, BC oldalt A1 és A2 pontokban metszi. Hasonlóan definiáljuk a B1,B2,C1,C2 pontokat. Mutassuk meg, hogy A1,A2,B1,B2,C1,C2 egy körön vannak. A kör középpontja a BC oldalfelezőpontja, és átmegy H-n, BC oldalt A1 és A2 pontokban metszi. Hasonlóan definiáljuk a B1,B2,C1,C2 pontokat. Mutassuk meg, hogy A1,A2,B1,B2,C1,C2 egy körön vannak.
2. x,y,z valós számok mindegyike különbözik egytől és xyz=1. Mutassuk meg, hogy 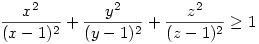 . Továbbá, hogy végtelen sok x,y,z racionális számhármasra az egyenlőtlenség egyenlőséggel teljesül. . Továbbá, hogy végtelen sok x,y,z racionális számhármasra az egyenlőtlenség egyenlőséggel teljesül.
3. Mutassuk meg, hogy végtelen sok pozitív egész n számra n2+1-nek van 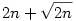 -nél nagyobb prímosztója. -nél nagyobb prímosztója.
|
|
|
| [42] sakkmath | 2006-08-07 11:49:30 |
 A képlet ugyanis hiányos! A helyes változat: az egyenlőtlenség bal oldalán álló kifejezés abszolútértékjelek között áll, a jobb oldali kifejezést pedig M-mel kell szorozni. Egyébként a mostani IMO honlapján is meg lehet találni a kitűzött feladatok magyar szövegét. A megoldásokat már csak angolul közlik. Üdv Mindenkinek!
|
| Előzmény: [41] nadorp, 2006-08-07 11:17:44 |
|
|
| [40] Kós Géza | 2006-08-07 11:03:56 |
 A feladatok.
Első nap
1. feladat. Az ABC háromszög beírt körének középpontja legyen I. A háromszög P belső pontja kielégíti a PBA +PCA +PCA =PBC =PBC +PCB +PCB egyenlőséget. Bizonyítsuk be, hogy AP egyenlőséget. Bizonyítsuk be, hogy AP AI, és egyenlőség akkor és csak akkor áll fenn, ha P=I. AI, és egyenlőség akkor és csak akkor áll fenn, ha P=I.
2. feladat. Legyen P egy szabályos 2006-szög. P egy átlóját jónak nevezzük, ha a végpontjai P határát két olyan részre bontják, amelyek mindegyike P páratlan sok oldalát tartalmazza. Az oldalakat szintén jónak nevezzük. Tegyük fel, hogy P-t háromszögekre bontottuk 2003 olyan átlóval, amelyek közül semelyik kettőnek nincs közös pontja P belsejében. Határozzuk meg az ilyen felbontásokban előforduló egyenlőszárú, két jó oldallal rendelkező háromszögek számának maximum át.
3. feladat. Határozzuk meg a legkisebb olyan M valós számot, amire az
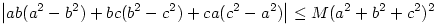
egyenlőtlenség teljesül minden a,b,c valós számra.
Második nap
4. feladat. Határozzuk meg az összes olyan, egész számokból álló (x,y) számpárt, amire teljesül 1+2x+22x+1=y2.
5. feladat. Legyen P(x) egy egész együtthatós, n>1 fokú polinom, és legyen k egy pozitív egész. Tekintsük a Q(x)=P(P(...P(P(x))...)) polinomot, ahol P k-szor fordul elő. Bizonyítsuk be, hogy legfeljebb n darab olyan t egész szám van, amire Q(t)=t.
6. feladat. Egy P konvex sokszög mindegyik b oldalához hozzárendeljük a legnagyobb területű olyan háromszög területét, aminek egyik oldala b és ami benne van P-ben. Bizonyítsuk be, hogy a P oldalaihoz rendelt területek összege legalább a kétszerese P területének.
|
| Előzmény: [39] Kós Géza, 2006-08-07 10:46:46 |
|
| [39] Kós Géza | 2006-08-07 10:46:46 |
 Úgy látom, a matekolimpikonok kicsit szégyenlősebbek, mert idén nem csillog annyira fényesen az eredmény (de azért mindenki nyert érmet).
|
1. |
2. |
3. |
4. |
5. |
6. |
összesen |
érem |
| Kis Gergely |
7 |
3 |
1 |
6 |
7 |
0 |
24 |
ezüstérem |
| Jankó Zsuzsanna |
7 |
7 |
0 |
6 |
3 |
0 |
23 |
ezüstérem |
| Erdélyi Márton |
7 |
7 |
0 |
7 |
1 |
0 |
22 |
ezüstérem |
| Nagy Csaba |
7 |
1 |
0 |
6 |
5 |
0 |
19 |
ezüstérem |
| Paulin Roland |
7 |
4 |
0 |
7 |
1 |
0 |
19 |
ezüstérem |
| Tomon István |
7 |
1 |
0 |
6 |
1 |
0 |
15 |
bronzérem |
|
|
|
|
|
|
|
|
|
| Estélyi István (Szolvákia) |
7 |
1 |
0 |
7 |
0 |
0 |
15 |
bronzérem |
|
Csapatban tizenhetedikek lettünk.
Az eredmények részletesebben itt olvashatók.
|
|
| [38] rizsesz | 2005-08-25 13:17:41 |
 Ja nem :) én úgy gondoltam, hogy kik az idei versenyzők, csak kétféle módon kérdeztem rá, én okos. Agysejtek rulez! És gratula n+1. alkalommal.
|
| Előzmény: [30] Zsuzsy, 2005-07-23 22:20:21 |
|
| [37] SAMBUCA | 2005-08-25 11:38:37 |
 CSáttok Arcok!
GRATULA MINDENKINEK!!!!!!!!!!!!!
Üdv. SAMBUCA ( egy ex HUN1 :P)
|
|
| [36] Zsuzsy | 2005-08-07 18:58:30 |
 Danke, de mi az hogy Alk.?
|
|
| [35] Edgar | 2005-07-30 22:20:17 |
 fizikus csapat == arc. szerintem.
Kár, hogy 1 ponton múlt a 3 magyar arany a matek nyesőn. Nem baj, jövőre Alk. Zsuzsi biztos kivágja a sárgarezet. Roller pedig alap :-D
Edgar 2004/5. példájában nem vitatható pont volt, hanem tetemes lyuk :-D Kétoldalról-csinálós-középen-elsumákolós. Szerintem. Valódi 42 pont azért nem könnyű biznissz, nemcsak mindent meg kell csinálni rendesen, de jó gyorsan is, és aztán tisztán leírni... le a kalappal azelőtt, aki nem koordinátori (javítói) hibából éri el ;-) A 42 ponttal való problémákat talán nem lehet jobban jellemezni, mint hogy az 1997-es aranycsapat két 41-et és egy 40-et is kapott...
|
|
| [34] Edgar | 2005-07-30 22:10:21 |
 2005-ös csapat = arc! Gratulálok! Csak amiatt vagyok kicsit bánatos, hogy ezek szerint nem volt túl hatékony az egyenlőtlenséges arzenál by Davids :'( El kellett volna mondanom a Muirhead-et!! Ha jól tudnék TeX-ben szedni, már fellőttem volna valahova. Ha még nem nyestem volna be, ez egy jókis oldal, tudtommal az egyetlen, ahol a részletes eredmények is ottfeszülnek régi olimpiákról: http://www.srcf.ucam.org/ jsm28/imo-scores/ Innen megtudható, kik milyen azonosítót viseltek, és pontosan mikre kapták a pontokat. 2005 Mérida még nincs rajta :-(
|
|
| [33] rizsesz | 2005-07-26 13:47:54 |
 Hát a fizikások is a papírforma szerint teljesítettek gondolom :) Illetőleg ott egy magyar diák, Halász Gábor holtversenyben a legtöbb pontot szerezte az abszolút versenyben! http://www.sulinet.hu/tart/cikk/ab/0/27409/1 Nekik is nagyon nagy gratula!
|
|
