Fórum: Matematikai Diákolimpia

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16]

Szeretnél hozzászólni? Jelentkezz be.

2011-07-18 15:25:22

IMO2011 / 1. nap

1. feladat: Az A={a₁,a₂,a₃,a₄} halmaz négy, páronként különböző pozitív egész számból áll. Az a₁+a₂+a₃+a₄ összeget jelöljük s_A -val, és jelölje n_A az olyan (i,j) párok (1 $\le$ i<j $\le$ 4) számát, amelyekre a_i+a_j osztója s_A -nak.

Határozzuk meg az összes olyan A halmazt, amelyre n_A a lehetséges maximális értékét veszi fel.

2. feladat: Legyen S a sík pontjainak egy véges, legalább kételemű halmaza. Feltesszük, hogy az S halmaz semelyik három pontja sincs egy egyenesen. Egy szélmalomnak nevezett folyamat során kiindulunk egy l egyenesből, amely az S halmaznak pontosan egy P pontját tartalmazza. Az egyenes a P középpont körül az óramutató járásával megegyező irányban forog addig, amíg először nem találkozik egy másik, S halmazba tartozó ponttal. Ekkor ez a Q pont lesz az új középpont, és az egyenes a Q pont körül forog tovább az óramutató járásával megegyező irányban egészen addig, míg újra nem találkozik egy S halmazba tartozó ponttal.

Ez a folyamat vég nélkül folytatódik.

Bizonyítsuk be, hogy megválaszthatjuk a P $\in$ S pontot és a P-n átmenő l egyenest úgy, hogy az S halmaz minden pontja végtelen sokszor legyen a szélmalom középpontja.

3. feladat: Legyen f : R $\to$ R egy olyan függvény, amelyre teljesül az

f(x+y) $\le$ yf(x)+f(f(x))

feltétel minden x,y valós számra. Bizonyítsuk be, hogy minden x $\le$ 0 esetén f(x)=0.

[81] Golyoska

2010-09-18 18:34:31

Én úgy tudom, hogy ez a csapat a "kicsi IMO" csapat, azaz ez segíti felhozni a jövő bajnokait. Ez jól látható a honlapjukon: http://memo.szolda.hu helyen is, ahol az is látható, hogy az elmúlt években több olyan diák is ennek a csapatnak a tagja volt korábban, aki utána az IMO csapatban ért el szép sikereket.

Az, hogy a Kenguru verseny szervezői támogatják ezt a csapatot, az nem von le semmit sem a csapat által elért eredmény értékéből. Tudtommal rajtuk kívül (Kenguru) csak a Bolyai Társaság támogatja még őket, a minisztérium nem. Pedig az utaztatás és versenyeztetés pénzigényes ... :)

Előzmény: [79] Róbert Gida, 2010-09-17 00:27:31

[80] Csimby

2010-09-17 12:37:19

Gratulálok a csapatnak!!

Itt a feladatsorok is megtalálhatók: katt

Előzmény: [79] Róbert Gida, 2010-09-17 00:27:31

[79] Róbert Gida

2010-09-17 00:27:31

http://index.hu/tudomany/2010/09/16/magyar_diakok_taroltak_a_kozep-europai_matekolimpian/

Az azért meglepett, hogy mindenféle ugribugri matekversenyeket is figyelembe vesznek a csapat összeállításnál.

[78] rizsesz

2010-07-30 12:06:18

És akkor már a fizika se maradjon el:

http://ipho2010.hfd.hr/tekst.php?id=32

3 magyar arany!

[77] rizsesz	2010-07-22 13:33:22
Művészet ennyire nem tudni csalni (már ha tényleg így történt). :) És egyben szomorú is azért, ha egy ilyen versenynél megkritizálható a tisztaság.
Előzmény: [75] Python, 2010-07-22 13:08:11

[76] Blinki Bill	2010-07-22 13:21:58
Ezek szerint előre meg lehet szerezni a példákat???!!!
Előzmény: [75] Python, 2010-07-22 13:08:11

[75] Python	2010-07-22 13:08:11
Néhányan a 3. feladatlapra vázlatok vagy más gondolkodásra utaló jelek nélkül rögtön kimondtak egy lemmát, úgy ahogy ez a hivatalos megoldásban szerepelt, és a szóbeszéd szerint a nyitóünnepségen a csapatvezető (aki már ismerte a feladatokat és megoldásokat) egy dossziét adott át a csapatvezetőhelyettesnek (aki a verseny előtt még találkozott a diákokkal).
Előzmény: [74] Blinki Bill, 2010-07-21 20:46:18

[74] Blinki Bill	2010-07-21 20:46:18
Miért?
Előzmény: [73] Róbert Gida, 2010-07-11 21:51:16

[73] Róbert Gida	2010-07-11 21:51:16
Pontosabban Észak-Korea.
Előzmény: [72] Róbert Gida, 2010-07-11 21:48:54

[72] Róbert Gida	2010-07-11 21:48:54
Dél koreaiakat megint kizárták.

[71] Kós Géza

2010-07-11 20:11:21

Az egyéni verseny eredménye

Csapatverseny

A magyarok pontszámai feladatonként

Előzmény: [70] Róbert Gida, 2010-07-11 18:01:54

[70] Róbert Gida

2010-07-11 18:01:54

Összesen 129 ponttal, megosztott 13. hely az országok ranglistáján. (Kína végül 197 ponttal nyert).

Bodor Bertalan: 15 pont (bronz)

Dankovics Attila: 21 pont (ezüst)

Éles András: 25 pont (ezüst)

Mészáros András: 11 pont (dicséret)

Nagy Donát: 29 pont (arany)

Nagy János: 28 pont (arany)

Előzmény: [69] Láda19, 2010-07-11 12:58:37

[69] Láda19	2010-07-11 12:58:37
A magyar csapat milyen eredményt ért el?
Előzmény: [68] Róbert Gida, 2010-07-10 22:58:00

[68] Róbert Gida

2010-07-10 22:58:00

1) Kína 190

2) Oroszország 169

3) USA 168

Előzmény: [67] rizsesz, 2010-07-10 11:09:41

[67] rizsesz

2010-07-10 11:09:41

Szia Géza!

Az eredmények mikorra várhatóak?

Előzmény: [66] Kós Géza, 2010-07-08 10:52:53

[66] Kós Géza

2010-07-08 10:52:53

Íme az idei feladatok.

Első nap

1. feladat. Határozzuk meg az összes olyan f:R $\to$ R függvényt, amelyre az

f([x]y)=f(x)[f(y)]

egyenlőség teljesül minden x,y $\in$ R-re. (Itt [z] a legnagyobb olyan egész számot jelöli, amely kisebb vagy egyenlő z-nél.)

Javasolta: Franciaország

2. feladat. Legyen I az ABC háromszög beírt körének középpontja, $\Gamma$ pedig a háromszög körülírt köre. Az AI egyenes másik metszéspontja a $\Gamma$ körrel legyen D. Legyen E a BDC körív egy pontja, F pedig a BC szakasz egy pontja, amelyekre teljesül

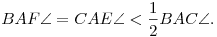
$BAF \angle = CAE \angle < \frac{1}{2} BAC \angle .$

Legyen továbbá G az IF szakasz középpontja. Bizonyítsuk be, hogy a DG és EI egyenesek a $\Gamma$ körön metszik egymást.

Javasolta: Hong Kong

3. feladat. Legyen N a pozitív egész számok halmaza. Határozzuk meg az összes olyan g:N $\to$ N függvényt, amelyre

(g(m)+n)(m+g(n))

teljes négyzet minden m,n $\in$ N-re.

Javasolta: USA

Második nap

4. feladat. Legyen P egy pont az ABC háromszög belsejében. Az AP, BP és CP egyenesek másik metszéspontja az ABC háromszög $\Gamma$ körülírt körével legyen rendre K, L és M. A $\Gamma$ körhöz C pontban húzott érintő messe az AB egyenest az S pontban. Tegyük fel, hogy SC=SP. Bizonyítsuk be, hogy MK=ML.

Javasolta: Lengyelország

5. feladat. A B₁,B₂,B₃,B₄,B₅,B₆ dobozok mindegyikében kezdetben egy érme van. Kétféle megengedett lépés van:

1. típusú lépés: Választunk egy B_j nemüres dobozt, ahol 1 $\le$ j $\le$ 5. Elveszünk egy érmét a B_j dobozból, és hozzáadunk két érmét a B_j+1 dobozhoz.

2. típusú lépés: Választunk egy B_k nemüres dobozt, ahol 1 $\le$ k $\le$ 4. Elveszünk egy érmét a B_k dobozból, és kicseréljük a B_k+1 (esetleg üres) doboz tartalmát a B_k+2 (esetleg üres) doboz tartalmával.

Állapítsuk meg, hogy ilyen lépések valamilyen véges sorozata segítségével elérhető-e, hogy a B₁, B₂, B₃, B₄, B₅ dobozok mindegyike üres legyen, a B₆ doboz pedig pontosan 2010^{2010²⁰¹⁰} érmét tartalmazzon. (Definíció szerint a^{b^c}=a^{(b^c)}.)

Javasolta: Hollandia

6. feladat. Legyen a₁,a₂,a₃,... pozitív valós számok egy sorozata. Tegyük fel, hogy van egy olyan s pozitív egész, amellyel

a_n=max {a_k+a_n-k | 1 $\leq$ k $\leq$ n-1}

teljesül minden n>s egészre. Bizonyítsuk be, hogy léteznek olyan $\ell$ és N pozitív egészek, amikre $\e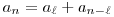ll$ $\leq$ s, és $a_n=a_\ell+a_{n-\ell}$ minden n $\geq$ N-re.

Javasolta: Irán

[65] janomo	2009-07-26 10:48:12
Hát sajnos nem sokal, egy egyszerű geot kellet volna megoldanom. De mondom, majd jövőre...
Előzmény: [64] Tibixe, 2009-07-25 23:56:48

[64] Tibixe	2009-07-25 23:56:48
Gratulálok én is. Jól látom, hogy nem sokkal maradtál le az aranyról?
Előzmény: [60] janomo, 2009-07-22 20:19:23

[63] lorantfy	2009-07-24 16:14:38
Gratulálok a csapat minden tagjának és a felkészítő tanároknak!

[62] Python	2009-07-23 12:32:55
Gratulálok a csapatnak!

[61] Láda19	2009-07-23 07:03:43
Biztosak vagyunk abban, hogy mindent megtettetek az eredményes szereplés érdekében. Mnd a hatan érmet szereztetek, ez szép teljesítmény. Gratulálok a csapatnak, és mindannyiótoknak további sikeres és eredményes munkát kívánok.
Előzmény: [60] janomo, 2009-07-22 20:19:23

[60] janomo	2009-07-22 20:19:23
Köszönjük. Megpróbáltuk a lejobbat kihozni magunkból. Jővőre megpróbálunk még jobbak lenni. Nagy János
Előzmény: [56] m2mm, 2009-07-19 14:25:26

[59] Láda19	2009-07-19 17:03:21
Köszönöm szépen!
Előzmény: [58] m2mm, 2009-07-19 16:33:24

[58] m2mm	2009-07-19 16:33:24
http://www.imo-official.org/year_info.aspx?year=2009
Előzmény: [57] Láda19, 2009-07-19 16:22:46

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16]

Már regisztráltál?
Új vendég vagy?