Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[1033] jenei.attila	2009-11-11 13:34:10
Ha képezed a a³+(a+1)³+...+(a+7)³ összeget, akkor elvégezve a köbre emeléseket és az összevonásokat, majd teljes köbre kiegészítve (számításokat nem részletezve) kapod, hogy a fenti összeg (2a+7)³+126a+441. Tehát nagyjából 2a+7 köbe. Ha a>-3,5 akkor kicsit nagyobb nála, ha a<-3.5, akkor kisebb nála. Az első esetben a kifejezésünk kisebb lesz mint (2a+8)³, ha teljesül a (2a+7)³+126a+441<(2a+8)³, vagyis két szomszédos köbszám közé fog esni, ezért nem lehet köbszám. Megoldva a fenti másodfokú egyenlőtlenséget azt kapjuk, hogy ha a<-3.49 vagy a>6.49 akkor az érték kisebb lesz mint (2a+8)³, ha viszont a>-3.5, nagyobb lesz mint (2a+7)³. Hasonlóan a másik esetben (ha a<-3.5) felírva a (2a+6)³<(2a+7)³+126a+441 egyenlőtlenséget, azt kapjuk, hogy az összeg értéke két szomszédos köbszám értéke közé esik, ha a<-13.49 vagy a>-3.51. Ezeket összevetve, és figyelembe véve hogy a egész, kapjuk, hogy -13 $\le$ a $\le$ kell hogy teljesüljön, ha az összeg köbszám.
Előzmény: [1032] jonas, 2009-11-11 13:06:20

[1032] jonas	2009-11-11 13:06:20
Honnan jön a korlát?
Előzmény: [1030] jenei.attila, 2009-11-11 08:42:44

[1031] jenei.attila	2009-11-11 11:20:32
Végig számoltam, és csak azok vannak, amiket jonas talált. Ekkor a=-5,-4,-3,-2.
Előzmény: [1030] jenei.attila, 2009-11-11 08:42:44

[1030] jenei.attila	2009-11-11 08:42:44
Ha a,a+1,...,a+7 a nyolc szomszédos egész szám amelyek köbeinek összegeként kell köbszámot előállítani, akkor -13 $\le$ a $\le$ 6 kell hogy teljesüljön. Ez 20 lehetséges eset, nem számoltam ki melyek adnak valóban köbszámot.
Előzmény: [1024] gabor7987, 2009-11-08 14:47:08

[1029] m2mm	2009-11-08 19:24:08
Ja, tényleg elnéztem. De x=5, y=4 megoldás... 2b²+1=3k²-re visszatérve: b₀=1, b₁=11, b_n=10b_n-1-b_n-2 sorozat a megoldása az egyenletnek. b₀ az er. feladatnak nem megoldása, mert x₀=0, de a többi jó.
Előzmény: [1027] HoA, 2009-11-08 18:13:59

[1028] HoA	2009-11-08 18:17:45
Persze a szöveges feladatnak nem megoldása x=y=0, mert csak a pozitív egészeket kéri.
Előzmény: [1027] HoA, 2009-11-08 18:13:59

[1027] HoA	2009-11-08 18:13:59
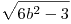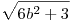Talán mégis. Ugyanis az x=y=0 megoldást nem zártuk ki, mégis elveszett útközben. Nekem $\sqrt{6b^2 -3}$ helyett $\sqrt{6b^2 +3}$ jön ki, de innen 6b²+3=c²=9k² ;2b²+1=3k² következik, ami b=k=1 -re még jó. 3k²-1 páros, k páratlan, k=2l+1, amiből b²=6l²+6l+1 adódik , körbeértünk. Talán elfogadva és a továbbiakból kizárva x=y=0 -t a legkisebb pozitív y-t kéne keresni, amiből kijönne, hogy csak akkor létezik, ha létezik nála kisebb pozitív l, vagyis sohasem.
Előzmény: [1025] m2mm, 2009-11-08 15:17:00

[1026] jonas	2009-11-08 16:17:37
Négyet könnyű találni: -216,-64,64,216. Csak azt kéne eldönteni, van-e még.
Előzmény: [1024] gabor7987, 2009-11-08 14:47:08

[1025] m2mm

2009-11-08 15:17:00

Ha nem számoltam el...

$x=\frac{-2+\sqrt{4+24y^2+24y}}{4}=\frac{-1+\sqrt{6y^2+6y+1}}{2}$ . Ha 6y²+6y+1 négyzetszám, csak akkor lesz nyilván x racionális, de 6y²+6y+1 négyzetgyöke páratlan, ezért a számláló páros, x egész. Tehát 6y²+6y+1=b²-et kell megoldani. $y=\frac{-6+\sqrt{24b^2+36-24}}{12}=\frac{-3+\sqrt{6b^2-3}}{6}$ . Ha $\sqrt{6b^2-3}$ egész, akkor páratlan, ráadásul hárommal osztható, azaz y egész: 6b²-3=c²-et kell megoldani. c osztható 3-mal:c=3k. 2b²-1=3k²-et kell megoldani. Ennek pedig nincs megoldása: bal oldal nem osztható 3-mal, de a jobb oldal igen.

Előzmény: [1021] Euler, 2009-11-08 11:48:21

[1024] gabor7987

2009-11-08 14:47:08

Ehhez a feladathoz hozzá sem tudok kezdeni. Tudna valaki segíteni?

Adjuk meg az összes olyan köbszámot, amely előáll nyolc szomszédos egész szám köbének az összegeként.

[1023] Alma	2009-11-08 13:26:18
Arra gondolsz, hogy nem kellett volna homogénnek feltételeznem a gravitációs erőteret? Lehet igazad van. Erre nem gondoltam.
Előzmény: [1019] Willy, 2009-11-08 00:33:39

[1022] Willy

2009-11-08 12:50:49

Szerintem meg elég egyértelmű, hogy mit kell csinálni. Leni vedd észre azt, hogy az F=m^.a az 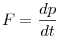$F= \frac {dp}{dt}$ egy olyan speciális alakja, amikor a tömeg állandó. Ez az általánosabb (látsd Landau1). Az F-et meg nyilván erőtörvényből kapjuk... és pont.

Amúgy elég érdekes feladat lenne az, ha 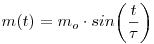$m(t)=m_o \cdot sin \bigg(\frac t \tau \bigg)$ tömegváltozást feltételeznénk. Vajon fellép-e bárminemű rezonancia?

Előzmény: [1020] leni536, 2009-11-08 10:46:32

[1021] Euler	2009-11-08 11:48:21
Sziasztok! Van egy diofantikus egyenletem, amelyet a pozitiv egész számok halmazán kellene megoldani,ha tud valaki, sagitsen,előre is köszönöm..Az egyenlet: 2x2+2x=3y2+3y

[1020] leni536

2009-11-08 10:46:32

Nekem nem tetszett nagyon ez a feladat, egy folytonosan változó tömegnél nincs sok esélye a tömegnövekménynek csak együtt mozogni az eredeti tömeggel, akár az F=ma-val, vagy az 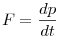$F=\frac{dp}{dt}$ -vel számolunk. Mivel nem tudjuk, hogy honnan jön a plusz tömeg, ezért nem tudhatjuk, hogy melyiket kell alkalmazni. Persze a feladat elég egyszerűnek minősülne, ha az F=ma-t kellene alkalmazni, így lehet sejteni, hogy a másikra van szükség, de akkor sem megalapozott, hogy az a helyes.

[1019] Willy	2009-11-08 00:33:39
Azon gondolkoztál, hogy mi van, ha $\tau$ nagy?
Előzmény: [1018] Alma, 2009-11-06 02:23:23

[1018] Alma

2009-11-06 02:23:23

Ennek a feldatnak a megoldását pont megírtam tex-ben, úgyhogy feltöltöm. Lehet, hogy valamit nagyon elnéztem, mert nekem gyanúsan egyszerűnek tűnik (nem nagyképűségből mondom, hanem a többi feladathoz képest).

Írjuk fel a test mozgásegyenletét!

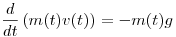
$\frac{d}{dt}\left(m(t)v(t)\right)=-m(t)g$

Behelyettesítve a feladat által megadott tömeg(idő) függvényt, a következő egyenlethez jutunk:

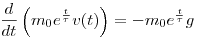
$\frac{d}{dt}\left(m_0e^{\frac{t}{\tau}}v(t)\right)=-m_0e^{\frac{t}{\tau}}g$

Elvégezve a deriválást és az egyszerűsítéseket:

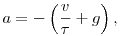
$a=-\left(\frac{v}{\tau}+g\right),$

ahol $a=\frac{dv}{dt}$ a test sebessége. Ez a sebességre nézve egy lineáris elsőrendű differenciálegyenlet. Szeparálva a változókat:

$-\frac{dv}{\left(\frac{v}{\tau}+g\right)}=dt.$

Mindkét oldalt határozottan integrálva a fellövés pillanatától t idővel későbbig:

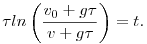
$\tau ln\left(\frac{v_0+g\tau}{v+g\tau}\right)=t.$

Ebből kifejezve a sebességet a felhajítástól eltelt idő függvényében:

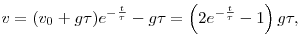
$v=(v_0+g\tau)e^{-\frac{t}{\tau}}-g\tau=\left(2e^{-\frac{t}{\tau}}-1\right)g\tau,$

felhasználva, hogy v₀=g $\tau$ a feladat szövege szerint. A test akkor van pályájának tetőpontján, amikor sebessége zérussá válik. Ezt a következőképp írhatjuk fel egyenlettel:

$v=\left(2e^{-\frac{t_{max}}{\tau}}-1\right)g\tau=0,$

ami akkor teljesül, ha t_max=ln2 $\tau$ . Így a test t_max=ln2 $\tau$ idő múlva jut pályájának tetőpontjára. Ekkor a test tömege a megadott képlet alapján

$m_1=m_0e^{\frac{t_{max}}{\tau}}=2m_0$

[1017] Geg

2009-11-05 13:59:25

Igen, szerintem is kell az a minusz elojel.

Ha pedig lefele dobjuk. akkor a megadott kezdeti feltetelt kielegito megoldas v=g $\tau$ , vagyis a sebesseg konstans.

Előzmény: [1016] SmallPotato, 2009-11-05 12:47:53

[1016] SmallPotato	2009-11-05 12:47:53
Hm. Lehet, hogy a levezetés a (kezdeti) sebesség és a nehézségi gyorsulás ellentétes irányán bukik meg. Eszerint g előjelét végig ellentétesre kéne cserélni. De akkor is felmerül a kérdés: lefelé (azaz v₀ és g egyező iránya esetén) el se lehet hajítani a testet? :-)
Előzmény: [1014] SmallPotato, 2009-11-05 09:13:17

[1015] SmallPotato

2009-11-05 09:19:04

Persze, hogy eltoltam, bocsánat:

$t=-\tau ln (g-\frac v \tau)+lnC$ alapján

$t= ln \frac {C}{(g-\frac v \tau)^\tau }$ , de ez a v=v₀=g $\tau$ esetén 0-vá váló nevező problémáján nem változtat.

Előzmény: [1014] SmallPotato, 2009-11-05 09:13:17

[1014] SmallPotato

2009-11-05 09:13:17

A Newton-törvény 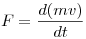$F=\frac {d(mv)}{dt}$ alakjából, a szorzás differenciálási szabályát alkalmazva

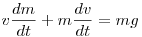$v \frac{dm}{dt}+m \frac{dv}{dt}=mg$ , azaz

$v\frac 1 \tau m_0 e^{\frac t \tau} + m_0 e^{\frac t \tau}\frac{dv}{dt}=m_0 e^{\frac t \tau}g$ , ahonnan (mivel $m_0 e^{\frac t \tau}$ nem lehet 0) kapjuk

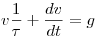$v\frac 1 \tau + \frac{dv}{dt}=g$ , azaz

$dv=(g-\frac v \tau)dt$ , vagy az integrálhatóság végett átrendezve

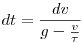$dt=\frac {dv} {g-\frac v \tau}$ .

Ennek megoldása

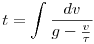$t=\int\frac {dv} {g-\frac v \tau}$ , azaz

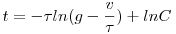$t=-\tau ln (g-\frac v \tau)+lnC$ , vagyis

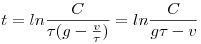$t= ln \frac {C}{\tau (g-\frac v \tau)}=ln \frac {C}{g \tau-v}$ .

Ha mármost C meghatározásához a kezdeti feltételt beírjuk:

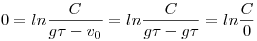$0=ln \frac {C}{g \tau-v_0}=ln \frac {C}{g \tau-g \tau}=ln \frac C 0$ , ahol is elakadtam rendesen.

Mondhatnánk, hogy 0 logaritmusa 1-nek van, tehát némi határérték-belemagyarázással C=0 lehetne, csakhogy ez a visszahelyettesítésnél ismét nem értelmezhető eredményhez (ln0) vezet.

Valahol biztosan rosszul látok valamit - de nem tudom, hol.

Előzmény: [1013] Lóczi Lajos, 2009-11-05 00:48:51

[1013] Lóczi Lajos	2009-11-05 00:48:51
Be tudnád írni a számolási részleteket?
Előzmény: [1012] SmallPotato, 2009-11-05 00:14:44

[1012] SmallPotato

2009-11-05 00:14:44

Tényleg szokatlan volt a változó tömeg ... pedig valóban csak vissza kellett volna nyúlni az eredeti Newton-törvényhez.

Tartok tőle, hogy ennek alapján magam is eljutottam az általad írt "csavar"ig ... legalábbis az integrálási konstans meghatározásába beletörött a bicskám. A szomorú az, hogy a szemlélet alapján nem látom a kiutat - a kezdeti feltétel nem abszurd, tehát megoldásnak igenis lennie kell, akkor is, ha nem látom.

Előzmény: [1011] Geg, 2009-11-04 22:59:08

[1011] Geg

2009-11-04 22:59:08

A feladatban Newton torvenyet kell alkalmazni: a testre hato ero megegyezik az idoegysegre juto impulzusvaltozassal. Tekintettel arra, hogy a tomeg nem allando, ezert a kozvetett fuggveny derivalasi szabalya alapjan lesz egy, a sebesseggel aranyos, a tomegvaltozas utemehez kapcsolodo tag is a szokasos m*a mellett. Az igy adodo differencialegyenletet kell megoldani a sebesseg-ido fuggvenyre.

Erdemes kicsit utanaszamolni. En most megtettem, es ha nem rontottam el, ezutan jon csak a csavar a feladatban.

Előzmény: [1010] SmallPotato, 2009-11-04 22:33:54

[1010] SmallPotato	2009-11-04 22:33:54
Nem relativisztikus tömegnövekedésről van szó. A feladat, amint azt Higgs a 997. hsz-ban megírta, itt található, az 5-ös számú.
Előzmény: [1009] Ergon, 2009-11-04 21:59:30

[1009] Ergon	2009-11-04 21:59:30
Ha feldobjuk a testet, akkor -mivel sebességre tesz szert-, már nem a nyugalmi tömeg lesz a tömege, hanem egy másik, annál nagyobb tömeg. Nem?

Már regisztráltál?
Új vendég vagy?