| [106] epsilon | 2006-12-03 19:40:06 |
 Helló! Gondolom, hogy a megoldást csak a valós számok halmazán keresed!? Miután bepötyöztem, akkor jelzi a fórum, hogy a "kalap" jelt nem használhatom hatvány gyanánt :-( Ezért az A második hatványát A)2-vel jelölöm Az értelmezési tartomány nyilván [-16,16], bevezetjük a 16+x=a)4 és 16-x=b)4 jelöléseket, így a+b=4 és a)4+b)4=32, ez egy szimmetrikus egyenletrendsyer, ezért az S=a+b és P=a×b jelölésekkel, a)2+b)2=S)2-2P, ebből a)4+b)4=S)4-4PS)2+2P)2, így az S=4 alapján a P)2-32P+112=0 egyenlet adódik, ahonnan P=4 vagy P=28. Ha P=4, S=4 mellett a, b a t)2-4t+4=0 megoldásai, vagyis a=b=2 => x=0. A P=28 esetben a,b a t)2-4t+28=0 ennek komplex T mgoldásai vannak, így a, b is komplex számok, és emiatt x-is.
|
| Előzmény: [105] Facsipesz, 2006-12-03 13:22:33 |
|
| [109] Doom | 2006-12-03 18:55:01 |
 Ha ez 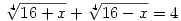 feladat, akkor itt egy megoldás (nem biztos, hogy a legrövidebb, viszont nincs kedvem töprengeni most szép megoldáson...) feladat, akkor itt egy megoldás (nem biztos, hogy a legrövidebb, viszont nincs kedvem töprengeni most szép megoldáson...)
Emeljük négyzetre, így kapjuk:
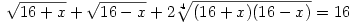
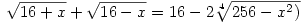
Újra négyzetre emelve:
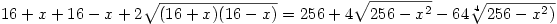
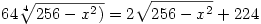
Vezessünk be új változót: 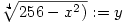 Ekkor Ekkor
64y=2y2+224
y2-32y+112=0
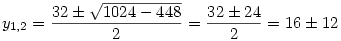
Azaz
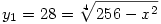
x2=-284+256=-614400
ami ellentmondás. A másik esetben
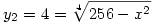
x2=-44+256=0
x=0
(Behelyettesítve kapjuk, hogy ez tényleg megoldás.)
|
| Előzmény: [105] Facsipesz, 2006-12-03 13:22:33 |
|
| [105] Facsipesz | 2006-12-03 13:22:33 |
 sziasztok, nagyon jól jönne egy kis segitség, nem tudom levezetni ezt a feladatot:
negyedik gyök alatt (16+x), plusz, negyedik gyök alatt (16-x), egyenlő, 4
(TeX kóddal nem engedte a parancsokat)
|
|
|
|
| [102] D_o_r_k_a | 2006-11-30 18:15:01 |
 1/3x2+3x + b/x2-2x + x/x2-x-2 = 0?????????????????????????Ez a házim és nem tudom megcsinálni! Segít valaki???Előre is köszi
|
|
| [101] Róbert Gida | 2006-11-30 14:59:06 |
 Sorozat tagjait azért fel lehet írni explicit alakban is, Fibonacci számokkal. Lévén csak az a,b kitevőit nézve a sorozat képzésénél a szorzás a kitevőknél összeadásba megy át.
|
| Előzmény: [97] S.Ákos, 2006-11-28 20:47:20 |
|
|
|
|
|
|
|
|
| [93] V Laci | 2006-11-18 18:36:36 |
 Köszönöm szépen! Bár jobban örültem volna valamilyen magyar nyelvű leírásnak, így legalább javíthatom az angol-tudásomat is. :)
|
|
|
|
| [90] V Laci | 2006-11-18 15:53:45 |
 Sziasztok! A Minkowski-összegekről szeretnék olvasni. Tudtok ajánlani valamit, ahol utánanézhetnék?
|
|
|
| [88] jonas | 2006-11-17 21:48:39 |
 Az elsőben nem vagyok biztos, mert már nagyon rég használtam deriveot, de ha jól emlékszem, a deriveban a változók alapból valósak, és külön meg kell mondani neki, hogy komplex legyen.
A másodikban azért nem, mert ha egy diák több jutalmat is kap, akkor a másodikban nem számolod 4!-szor. Ha például egy diák között kell szétosztani a négy jutalmat, akkor mindkét esetben csak egy lehetőség van.
|
| Előzmény: [82] phantom_of_the_opera, 2006-11-11 14:55:08 |
|
|
|
| [85] S.Ákos | 2006-11-15 18:55:38 |
 sziisztok! az lenne a kérdésem, hogy (|x|)'=sgnx helyes-e?
|
|
| [84] Hajba Károly | 2006-11-14 09:03:01 |
 Szia Gábor!
Balra fenn az 5 db okker menűpont középső a TeX tanfolyam. Tanulmányozd!
y=Ax2+Bx+C
Az origón átmenő x=3 'függőleges' azaz az y-tengellyel párhuzamos egyenes a parabola szimmetriatengelye. Ebből következik, hogy balra, azaz a negatív irányban amilyen messze van az egyik metszéspont, jobbra, azaz pozitív irányban ugyanolyan messze lesz a másik metszéspont. Azaz x1=0; x2=2*3=6
Mivel az parabola átmegy az origón O(0,0), így a parabola egyik pontja P(x=0,y=0). => 0=A*02+B*0+C. Ez csak akkor igaz, ha C=0. Tehát az egyenletünk y=Ax2+Bx(+0) formára egyszerűsödött. Ismerünk két másik fix pontot is P1(3,-2) és P2(6,0)-t. Ezek segítségével a redukált egyenletből fel tudsz állítani egy kétváltozós kétismeretlenes egyenletrendszert. Ennek elvégzése már nem bonyolult és szerintem te is el tudod végezni.
Kellemes munkát!
|
| Előzmény: [83] Gábor5, 2006-11-13 20:01:51 |
|
| [83] Gábor5 | 2006-11-13 20:01:51 |
 AZ y= a*x*x+b*x+c (az x négyzetet nem engedte máshogy )parabola átmegy az origón, a csúcspontja (3,-2). 1.Határozd meg az x-tengellyel való másik metszéspontot. 2. a; b; c=? Tudna valaki segíteni.
|
|








 R
R 


