| [1196] mologa | 2010-05-26 16:49:44 |
 2. Igazolja, hogy a minta normális eloszlású Adja meg a khi2 statisztika értékét ha az osztályok száma öt?
-1.48 , -1.48 , -1.45 , -1.06 , -1.05 , -1.04 , -1.04 , -0.94 , -0.94 , -0.75 , -0.70 , -0.55,-0.53 -0.48 , -0.38 , -0.09 , -0.05 , 0.04 , 0.05 , 0.11 , 0.18 , 0.19 , 0.32 , 0.36 , 0.48 , 0.51 , 0.60 0.70 , 0.70 , 0.83 , 1.30 , 1.50 , 2.08
minta elemszáma n = 33 A becsült paraméterek (átlag)=-0.123 korrigált szórás S csillag= 0.8886 Az osztályok száma r = 5
Egy osztály szélessége S csillag= 0.8886 Az osztály szélességre miért a (szórást) 0.8886 ot veszi?
Osztály közök Pi nPi
- - 1.4559 2 0.0668 2.2044 0.0190
-1.4559, -0.5673 9 0.2417 7.9761 0.1344
-0.5673, -0.3213 12 0.3830 12.639 0.0323 -0.3213, -1.2099 7 0.2417 7.9761 0.1195
-1.2099, - 3 0.0668 2.2044 0.2871 khi2=0.5893 Az osztályközök értéki miért igy jöttek ki? Ezt nem értemL Valaki levezeti
|
|
|
| [1194] mologa | 2010-05-26 16:40:15 |
 Sajnos nem tudom bemásolni a word-ben irt feladatot. Mig TeX-ben irnám meg kirügyeznék:))
|
|
|
|
|
| [1190] Hölder | 2010-05-23 23:49:40 |
 Sziasztok! Azon gondolkodtam el,hogy ha 2(n)+1 prim (kitevőben van az n), akkor n kettő hatvány (Fermat primek),de forditva igaz -e, azaz, ha n kettőhatvány,akkor 2(n)+1 prim, megnéztem egy jó ideig,addig igaz volt,az a sejtésem, hogy nem az.
|
|
|
|
|
|
| [1185] jonas | 2010-05-21 11:56:08 |
 A Poisson közelítést a binomiális eloszlásra akkor lehet használni, ha várhatóan kevés rossz üveg készül, például abban az esetben, amit Sirpi javasolt.
|
| Előzmény: [1182] Yvi, 2010-05-20 23:38:21 |
|
| [1184] Maga Péter | 2010-05-21 11:43:15 |
 A páros esetben  (2k)= (2k)= 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen  (3), (3), (5),... a kérdéses értékek, ezek tetszőleges pontossággal kiszámolhatók, akár a (5),... a kérdéses értékek, ezek tetszőleges pontossággal kiszámolhatók, akár a  , az e, a , az e, a  (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a  páratlan értékei, illetve ha nem, akkor esetleg más konstansokkal ( páratlan értékei, illetve ha nem, akkor esetleg más konstansokkal ( , e stb.) összefüggésbe hozhatók-e. A , e stb.) összefüggésbe hozhatók-e. A  -ról sem tudjuk, hogy racionális-e, és azt sem tudjuk, hogy -ról sem tudjuk, hogy racionális-e, és azt sem tudjuk, hogy  +e racionális-e (ha az lenne, akkor az e ugyanúgy kifejezhető lenne a +e racionális-e (ha az lenne, akkor az e ugyanúgy kifejezhető lenne a  -ből, mint a -ből, mint a 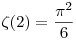 ), mégsem használjuk egyikre sem, hogy nem ismert. ), mégsem használjuk egyikre sem, hogy nem ismert.
|
| Előzmény: [1176] jenei.attila, 2010-05-20 19:36:13 |
|
|
| [1182] Yvi | 2010-05-20 23:38:21 |
 A binomiális eloszlással hogy jött ki a 803? Tényleg nem Poisson, csak elnéztem, az volt, oda írva, hogy a Poisson közelítést kell használni. Ez jelenti azt, hogy np=lambda?
|
| Előzmény: [1177] jonas, 2010-05-20 21:39:13 |
|
| [1181] jonas | 2010-05-20 22:57:29 |
 Persze nem kell nagyon komolyan venni ezt a tankönyvi példát, mert a válasz nagyon érzékeny az adatokra, mint pl. a szórás pontos értékére, a sör mennyiségének az eloszlására, meg az egyes üvegek függetlenségére. Ha egy kicsit módosítod a számokat, kaphatsz 0.1-et vagy 0.999-et is eredménynek.
|
| Előzmény: [1180] jonas, 2010-05-20 22:51:22 |
|
|
| [1179] Sirpi | 2010-05-20 22:40:07 |
 Szerintem el lett írva az átlag (51 helyett 50 kellene), mert úgy szimmetrikus a két határszám (48,9 és 51,1). És úgy valószínűleg értelmes lesz az eredmény is, ami kijön.
|
| Előzmény: [1177] jonas, 2010-05-20 21:39:13 |
|
| [1178] Higgs | 2010-05-20 22:20:09 |
 http://www.newscientist.com/article/dn18886-impossible-motion-trick-wins-illusion-contest.html
A valóságban is ezt a hatást keltené?
|
|
| [1177] jonas | 2010-05-20 21:39:13 |
 Ezt két lépésben kell megoldani. Először azt kell kiszámítani, hogy egy üveg sör mikor lesz hibás.
Annak a valószínűsége, hogy 48.9-nál kevesebb sör van az üvegben, elhanyagolhatóan kicsi, viszont mivel az átlag közel van, az 51.1-nél több sörnek egy üvegnél kb. 0.401 a valószínűsége. (Itt nyilván azt tettük föl, hogy a sör űrtartalma normális eloszlású.)
Ezért aztán a napi 2000 üvegből átlagosan 803 hibás van, tehát a binomiális eloszlást nem Poisson, hanem normális eloszlással kell közelíteni. Annak a valószínűsége, hogy 20-nál kevesebb túl nagy üveg sör készül, e miatt nagyon kicsi (értsd: előbb romlik el a gép), ha jól számolok, akkor 5.10-556 nagyságrendű.
(Nem vagyok túl jó statisztikából, úgyhogy valaki ellenőrizze a számításaimat.)
|
| Előzmény: [1175] Yvi, 2010-05-20 19:17:32 |
|
| [1176] jenei.attila | 2010-05-20 19:36:13 |
 A első probléma a Bernoulli-féle hatványösszeg probléma, amelyre egy nagyon szép levezetést találhatsz pl. Dörrie A diadalmas matematika c. könyvében. Egyébként magad is könnyen levezetheted, ha feltételezed, hogy a k-adik hatványok összege n-nek (a tagszámnak) egy k+1-ed fokú polinomja. Ekkor a polinomot határozatlan együtthatókkal felírva, n helyére 1,2,...k+2-őt helyettesítve, egy lineáris egyenletrendszert kapsz az együtthatókra. Az hogy a zárt képlet n-nek k+1-ed fokú polinomja, könnyen látható abból, hogy pk(n+1)-pk(n)=nk (ahol pk(n) a zárt alak n tagra) egy k-ad fokú polinom. Márpedig egy k+1-ed fokú polinom két egymás melletti természetes számon felvett helyettesítési értéke k-adfokú polinom. Tehát ha a fenti egyenletrendszernek van megoldása, akkor az megadja a zárt képletet is. Ennél egy lényegesen szellemesebb levezetést találsz az említett könyvben. A második probléma jóval nehezebb, és semmi köze az elsőhöz. Tudomásom szerint páros k-kra ismert zárt alak (k=2-re Euler adta meg először), míg páratlanokra nem ismert (ha nem így van, nyugodtan javítsatok ki).
|
| Előzmény: [1173] D. Tamás, 2010-05-20 19:08:29 |
|
| [1175] Yvi | 2010-05-20 19:17:32 |
 Köszönöm a segítséget, itt van egy utolsó példa, nagyon hálás lennék ha arra is elmondaná a megoldást valaki, aztán már abba is hagytam: Ha egy gép napi 2000 üveg sört gyárt, akkor mi a valószínűsége, hogy a nem 48.9 és 51.1 cl sört tartalmazó üvegekből maximum 20 készül el egy napon. (átlag: 51 cl és szórás: 0.4 cl, de nem tudom, hogy ezekre az adatokra szükség van-e? A feladatgyűjtemény mindenesetre azt írja, hogy ez Poisson-eloszlás)
|
| Előzmény: [1172] leni536, 2010-05-20 14:57:55 |
|
|
| [1173] D. Tamás | 2010-05-20 19:08:29 |
 Felmerült bennem a következő probléma: Több összeg meghatározásánál nagyon jól jönnek az ún. véges számsorok összegei. Például a számtani sorozat 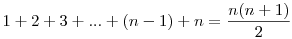 vagy az első n négyzetszám összege vagy az első n négyzetszám összege 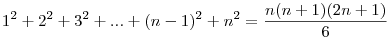 illetve ismertnek számít még a illetve ismertnek számít még a 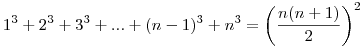 összefüggés is. összefüggés is.
És persze még folytathatnánk a sort, de jogosan merül föl a kérdés, hogy miképpen lehetne felírni az 1k+2k+3k+...+(n-1)k+nk összeget n függvényében. Ez lenne először is a legelső kérdésem, mert szerintem az algebrában biztosan egy kivesézett téma, de mégsem találtam hozzá forrást egy könyvben sem erről. Sajnos amilyen bizonyításokat ismerek ezekre az összefüggésekre, azokban mindig tettünk egy észrevételt, s miután "kiokoskodtuk" a helyes összefüggést teljes indukcióval beláttuk, így n-re ez nem teljesen használható. A következő ami szorosan kapcsolódik ehhez, az a reciprokösszeg. Tehát ha tekintjük az 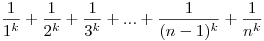 összeget, akkor mi a sorozat határértéke, ha k összeget, akkor mi a sorozat határértéke, ha k N? k=1 esetén ismert a probléma, ekkor a határértéke N? k=1 esetén ismert a probléma, ekkor a határértéke  , illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték , illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték 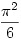 . No de hogyan lehetne felírni a határértéket k függvényében? . No de hogyan lehetne felírni a határértéket k függvényében?
|
|
| [1172] leni536 | 2010-05-20 14:57:55 |
 X N(64,162) N(64,162)
Ez ugye egy pontszám alakulásának a valószinűségi változója. Tudjuk, hogy egy diák 0,1 valószínűséggel bukik meg. Legyen x0 a bukás ponthatára, így:
P(X<x0)=0,1
Standardizálva az X-et:
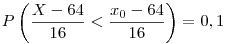
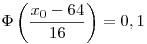
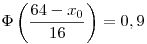
A standard eloszlást táblázatából:
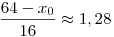
x0 43,52 43,52
Tehát jó közelítéssel 43 ponttal még buknak, 44-gyel már nem.
|
| Előzmény: [1171] Yvi, 2010-05-20 13:25:08 |
|






 (3) rac. együtthatós polinomjaként kifejezhető páratlan k-kra is
(3) rac. együtthatós polinomjaként kifejezhető páratlan k-kra is 
 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen
2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen  (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a
(Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a 
 N? k=1 esetén ismert a probléma, ekkor a határértéke
N? k=1 esetén ismert a probléma, ekkor a határértéke  , illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték
, illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték 
 N(64,162)
N(64,162)  43,52
43,52