Fórum: Valaki mondja meg!

Nem Gauss kvadratikus reciprocitás tétel ?

Köszönöm, sikerült (megint) elírnom, amire gondoltam.

Euler kritérium ellenőrzéséhez nem kell semmilyen prímfelbontást meghatároznod.

Hadd foglaljam röviden össze a helyzetet, mert volt némi keveredés.

Bármilyen p prímre az 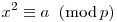kongruencia a számok kb. felére oldható meg (a p-hez nem osztható számoknak pontosan a felére, plusz még a p-vel osztható számokra). Összetett számokra nem ez a helyzet, itt több a számra nem oldható meg a kongruencia, mivel lényegében szétesik több másodfokú kongruenciára minden prímosztóra; hogy hány a-ra van megoldás, az így a p prímfelbontásából könnyen kiszámolható.

A p négyes maradéka abban segít, hogy eldöntsd, konkrétan x²-1 megoldható-e. Van arra is elmélet, hogyan lehet meghatározni, hogy egy bizonyos a-ra és p-re meg lehet-e oldani a kongruenciát, ehhez „csak” néhány (max (|a|,|p|)-nél kisebb vagy egyenlő) szám prímfelbontását kell tudni kiszámolni. Ebből az is következik, hogy rögzített a-ra és változó p prímekre a megoldhatóság csak p-nek a 4a-s osztási maradékától függ. Ez az Euler-féle kvadratikus reciprocitási tételen alapul, számelmélet kurzuson tanítani szokták, és le van írva a remek Erdős–Surányi-féle Válogatott fejezetek a számelméletből könyvben.

Egyre zöldebbeket írtok. Ha például a=1, akkor a kongruencia mindig megoldható, még az sem kell, hogy p prím.

Amúgy a kongruencia pontosan akkor oldható meg, ha 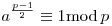, illetve, ha a osztható p-vel. (Ez van páratlan p prím esetén, p=2-re mindig van megoldás.) Mellesleg ez az Euler kritérium.

szerintem p maradéka mod 4. 4k+1 alakú prímekre mindig megoldható, 4k-1 alakúra nincs megoldás. A tételnek szerintem nincs külön neve.

p maradéka mod 4p az ránézésre p. De nem egészen értem a kérdést.

Üdv!

Valaki tudja, hogy mi a neve a következő tételnek: Az x²a(mod p) kongruencia akkor és csak akkor oldható meg (p prím), ha p maradéka egy (mod 4p) meghatározott halmazba tartozik?

Sőt, tetszőleges L^p-ben is igaz ez p>1-re (Hunt, nem sokkal Carleson után). A vicces az, hogy disztribúciós értelemben L¹-beli függvényhez is konvergál a Fourier-sora, ez nem nehéz, csak a fogalmakat kell ismerni.

Szia!

Ha van a térben teljes ortonormált rendszer (azaz olyan rendszer, hogy a különböző elemek skalárszorzata 0 és minden elem normája 1), akkor az eszerint vett Fourier-sor konvergens.

Továbbá L²-ben (a négyzetesen integrálható függvények terében) minden Fourier-sor (majdnem mindenütt) konvergens (ez Carleson tétele).

Kiestem a gyakorlatból, ezért egyszerű analízisbeli kérdésekkel fogok fordulni Hozzátok.

Fourier-sorokra néhány egyszerű konvergencia-kritériumot tudnátok adni?

(A félérintős elegendő feltételre és a Fejér-féle szigma összegzésre emlékszem alapkollégiumról)

Köszönöm!

Nem lehet véletlen, hogy Tao ilyen szintű problémákat soha nem feszeget a blogján...

"Páratlan számok prímtényezői csak páratlan számok lehetnek. Bizonyította ezt már valaki tételként?"

Nagyon mély sejtésnek tűnik. Kérdezd meg talán bily71-et a Goldbach sejtéses topikban!

"Hol a hiba a fenti statisztikában?"

Azt gondolom, hogy ott, hogy itt a relatív gyakoriságokat nincs értelme használni, mert végtelen/végtelen alakú határozatlan kifejezésre vezetnek.

Pontosan!

és még meglepőbb: ugyanannyi n-nel osztható szám van, mint racionális (n legyen egész) :)

"Gyakorlati jelentősége talán az lenne, hogy a gyors prímtényezős fölbontás algoritmusának valószínűleg úgy kellene kezdődnie, hogy a páros számokat addig kell osztani 2-vel, amíg egy páratlan számot nem kapunk, illetve (azután) a páratlan számok prímtényezőit csak a páratlan számok között kell keresni." Igen, ezt így is szokás csinálni!

Mondok valami meglepőt: páros számból éppen ennyi van, mint egészből! ;)

Az 1226-os hsz-edben bizonyítottad! ;-)

Úgy gondolom igazad van Jonas.

Én is hasonló gondolatra jutottam, és ezzel kapcsolatban jutott eszembe az alábbi sejtés:

Páratlan számok prímtényezői csak páratlan számok lehetnek.

Bizonyította ezt már valaki tételként?

Gyakorlati jelentősége talán az lenne, hogy a gyors prímtényezős fölbontás algoritmusának valószínűleg úgy kellene kezdődnie, hogy a páros számokat addig kell osztani 2-vel, amíg egy páratlan számot nem kapunk, illetve (azután) a páratlan számok prímtényezőit csak a páratlan számok között kell keresni.

Az a hiba, hogy a páros számok nincsenek ugyan többen, de általában többféleképpen írhatók fel két szám szorzataként, mint a páratlanok, mert általában több prímtényezőjük van.

A prímszámok kivételével minden szám fölírható két (másik) szám szorzataként.

1. Két páros szám szorzata páros számot ad.

2. Páros-páratlan szorzata páros számot ad.

3. Páratlan-páros szorzata páros számot ad.

4. Páratlan-páratlan szorzata páratlan számot ad.

Föntiekböl statisztikát készítve: háromszor annyi páros szám van mint páratlan - ami nyivánvalóan nem igaz.

(Mondhatnák, hogy a páros-páratlan szimmetriát a prímszámok billentik helyre, mert a 2 kivételével mind páratlan, de ez sem igaz mert a nagy számok felé haladva a prímszámok előfordulása egyre ritkább, a páros-páratlan szimmetria viszont a természetes számok sorában egyenletesen fönáll.)

Hol a hiba a fönti statisztikában?

Igazad van, köszönöm a választ.

Ott, hogy a dolog így szimmetrikus:

páros + páros = páros

páros + páratlan = páratlan

páratlan + páros = páratlan

páratlan + páratlan = páros

Úgy gondolom, az hogy egy számot többféleképpen is elő lehet állítani, mint két másik szám összegét - még nem cáfolja ezt a statisztikus megközeleítést.

Inkább úgy gondolom az lehet az ok, hogy a természetes számok sora nem úgy áll elő, hogy számokat véletlenszerűen összeadunk, hanem úgy hogy a kiindulási ponthoz az 1-hez (vagy a 0-hoz - ízlés szerint) hozzádunk 1-et, azután megint 1-et és így tovább.

ott h egy számot nem csak egyféle módon lehet előállítani két szám összegeként, és ez a statisztikai gondolkodás csak akkor működne.