| [1372] bily71 | 2010-09-21 17:21:48 |
 Mondanál egy példát arra, hogy úgy sikerült bizonyitani valamely természetes számokból álló sorozat végtelen voltát, hogy a tagok reciprokainak részösszegének sorozata irracionális számhoz tart? Egyátalán, hogy lehetünk ebben biztosak, mig nem tudjuk, hogy véges-e, vagy végtelen? (Egy rac. szám lehet két nagyon-nagyon nagy egész szám hányadosa is.)
Én nem azt mondom, hogy közelebb kerülnénk a Brun-konstans problémájának megoldásához, hanem azt, hogy ha tisztáztuk az ikerprim-kérdést, akkor elkezdhetjük a vizsgálódást, addig nem. Ha tévedek, légy szives javits ki, de ne úgy, hogy: "nincs igazad".
|
| Előzmény: [1368] Maga Péter, 2010-09-21 11:36:43 |
|
| [1371] Maga Péter | 2010-09-21 11:56:35 |
 Még egy érdekesség: van olyan végtelen játék, ahol egyik félnek sincs nyerő stratégiája, ami egy kicsit furcsa a véges játékokhoz szokott szemnek. Ennek bizonyítása a kiválasztási axiómán múlik. Ez az egyik szép példája annak, hogy a kiválasztási axióma -- hasson bármily természetesnek -- elég erős, nagyon-nagyon nem természetesnek ható következményekkel bír.
|
| Előzmény: [1370] Maga Péter, 2010-09-21 11:52:51 |
|
| [1370] Maga Péter | 2010-09-21 11:52:51 |
 A válasz az, hogy  ' létezik, azaz az irracionálisba hajtó játékosnak van nyerő stratégiája. Két egyszerű módszere is van. Az egyik az, hogy választ egy irracionális számot, és annak a jegyeit írja be, függetlenül attól, mit tesz a másik. Egy másik módszer pedig az, hogy sorbarendezi a racionális számokat, és az n. lépésében arra figyel, hogy az n. racionális számot elkerülje. Persze mindkettőt meg lehet formalizálni az előző hsz-emben levő módon ( ' létezik, azaz az irracionálisba hajtó játékosnak van nyerő stratégiája. Két egyszerű módszere is van. Az egyik az, hogy választ egy irracionális számot, és annak a jegyeit írja be, függetlenül attól, mit tesz a másik. Egy másik módszer pedig az, hogy sorbarendezi a racionális számokat, és az n. lépésében arra figyel, hogy az n. racionális számot elkerülje. Persze mindkettőt meg lehet formalizálni az előző hsz-emben levő módon ( '-kel). '-kel).
|
| Előzmény: [1369] Maga Péter, 2010-09-21 11:48:55 |
|
| [1369] Maga Péter | 2010-09-21 11:48:55 |
 A végtelen játék egy absztrakció. Ne úgy képzeld el, hogy két játékos játssza, hanem úgy, hogy minden végtelen tizedestört a Q vagy a Q' halmazban van aszerint, hogy racionális vagy irracionális. A kérdés az, hogy van-e olyan,  (illetve (illetve  ' függvény), ami a tizedesvessző utáni első páros sok (páratlan sok) számjegyhez rendel egy számjegyet úgy, hogy a ' függvény), ami a tizedesvessző utáni első páros sok (páratlan sok) számjegyhez rendel egy számjegyet úgy, hogy a
0, (Ø)a2 (Ø)a2 ( ( (Ø)a2)a4 (Ø)a2)a4 ( ( (Ø)a2 (Ø)a2 ( ( (Ø)a2)a4)... (Ø)a2)a4)...
(illetve
0,a1 '(a1)a3 '(a1)a3 '(a1 '(a1 '(a1)a3)a5...) '(a1)a3)a5...)
szám minden a2,a4,... sorozatra racionális (illetve a1,a3,... sorozatra irracionális). A Q és Q' halmazok diszjunktsága miatt  és és  ' nem létezhet egyszerre. Kérdés: létezik-e valamelyik, ha igen, melyik? ' nem létezhet egyszerre. Kérdés: létezik-e valamelyik, ha igen, melyik?
|
| Előzmény: [1342] bily71, 2010-09-20 14:51:06 |
|
| [1368] Maga Péter | 2010-09-21 11:36:43 |
 ,,"Az ikerprímsejtés bebizonyításával semmivel nem jutsz közelebb Brunhoz..."
De igen! (...)''
De nem! RG-nek van igaza. Képzeld azt, hogy bebizonyítottad az ikerprím-sejtést (mondjuk valamelyik bizonyításod jó a szomszéd topicban:P -- bocs, de nem lehetett kihagyni:)). Mivel lettél közelebb a Brun-konstans (ir)racionalitásához? (Nem számítva most egy olyan bizonyítást az ikerprím-sejtésre, amelyik közvetlenül az irracionális reciprokösszeget adja. Egy olyan persze valóban közelebb vinne...)
|
| Előzmény: [1367] bily71, 2010-09-21 09:24:46 |
|
| [1367] bily71 | 2010-09-21 09:24:46 |
 "Az ikerprímsejtés bebizonyításával semmivel nem jutsz közelebb Brunhoz..."
De igen! Ugyanis a végtelen sok tag SZÜKSÉGES feltétele az irracionalitásnak. Ha bebizonyosodik, hogy végtelen sok van belőlük, akkor már ELKEZDHETJÜK vizsgálni a Brun-állandót. Pl.: páratlan s esetén a zeta-függvény vizsgálatának azért van értelme, mert TUDJUK, hogy végtelen sok tagú összegről van szó. Véges sok tagnál fel sem merülne a kérdés.
|
| Előzmény: [1366] Róbert Gida, 2010-09-21 01:31:20 |
|
| [1366] Róbert Gida | 2010-09-21 01:31:20 |
 "Ha már tudjuk, hogy végtelen sok van belőlük, akkor már két alternativánk lesz."
? Most is 2 alternativánk van, vagy rac vagy irrac. Az ikerprímsejtés bebizonyításával semmivel nem jutsz közelebb Brunhoz, marad a 2 alternatíva.
Gondolkodásod meg olyan, mintha azt mondanánk, hogy amíg a Marsról nem tudunk mindent addig egyetlen exobolygót se vizsgáljunk az űrteleszkópokkal. Sehol nem tartana a csillagászat.
|
| Előzmény: [1360] bily71, 2010-09-20 21:30:24 |
|
|
|
|
|
|
|
|
| [1358] Fannka | 2010-09-20 21:19:19 |
 Hát mindenesetre köszönöm a válaszokat! És nincs semmi problémám azzal, h házit kell csinálnom, sőt kifejezetten jó feladatok ezek:) Nem lustaságból írom fel ide, pusztán ciki lenne nem megoldani a feladatot, meg a többiek is számítanak rám... A 7végén sokat gondolkodtam rajta, és nem jutottam semmire... Az órai feladatokat értem, sőt java részét magamtól is megoldom, de azok közt nincs (vagy én nem látok) ezekhez hasonló. De attól még ugyanúgy gondolkodom ezeken, mert vannak kevésbé izgi órák, amiket ennek szentelek:P Szóval akkor bocs, h ilyenekkel botránkoztattam meg itt a segítőkész embereket, ezentúl megtartom magamnak a kérdéseim. (Ui.: Milyen logika az, h azok tartanak össze, akiknek kutya a szimbólumok?)
|
 |
|
|
|
| [1355] Róbert Gida | 2010-09-20 20:43:26 |
 Nem látom, hogy miért ne vizsgálhatnánk, hogy rac. vagy irrac. Abban igazad van, hogy irrac csak úgy lehet, ha végtelen sok ikerprím van (amit sejtünk), de rac. nem csak úgy lehet, ha véges sok ikerprím van, hiszen egy végtelen sok tagú poz. sor összege is lehet rac: 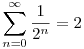
|
| Előzmény: [1350] bily71, 2010-09-20 17:03:25 |
|
| [1354] Sirpi | 2010-09-20 20:26:15 |
 Mivel ez nem egy fizikapélda, nem különösebben. Szerintem amúgy is zavaróbb, hogy nincs végtelen sok atom a világegyetemben a kapott szám megjelenítéséhez. Ez csak egy szemléltetés, hogy hogy lehet ilyesmit elképzelni, de a valóságban nyilván senki nem fog nekiállni ilyet játszani.
|
| Előzmény: [1348] Róbert Gida, 2010-09-20 15:29:43 |
|
| [1353] bily71 | 2010-09-20 19:25:18 |
 Valóban, nem szerepel az összes rac. illetve irrac. szám. Azt én is tudom, hogy nincs, (Cantor bizonyitása nem olyan bonyolult, hogy ne érteném), csak játszom a gondolattal.
Képezzünk egy fát a következőképp: az első csúcsot cimkézzük fel a 0-val. Az első csúcsból induljon 10 él 10 csúcsba, cimkézzük fel az új csúcsokat a 0-tól 9-ig terjerdő természetes számokkal, úgy, hogy a baloldali kapja a 0-t, a mellette lévő az 1-est, és igy tovább, vagyis mindegyik új csúcs különböző számú cimkét kapott. Az új csúcsok mindegyikéből induljon 10 él 10 új csúcsba, ezeket a csúcsokat is az előbbiekhez hasonlóan cimkézzük fel. Azután ezekből a csúcsokból is induljon..., és igy tovább
Ime, itt van az összes [0,1] intervallumba eső valós szám, ugyanis, ha elindulunk a kezdőcsúcstól, végigmegyünk valamelyik úton és leirjuk egymás után, hogy melyik számokat érintettük, úgy, hogy az első 0 után egy tizedesvesszőt irunk, akkor egy valós számot kapunk. Ha csak 0-kat , akkor a 0-t, ha csak 9-eseket érintünk, akkor az 1-et kapjuk eredményül. (A 0-n és az 1-en kivül minden racionálist kétszer kaptunk meg, pl.: 0.5999...=0.6.)
Megszámlálható-e bejárható utak halmaza?
|
| Előzmény: [1352] Alma, 2010-09-20 18:04:29 |
|
|
| [1351] bily71 | 2010-09-20 17:51:27 |
 Tudjuk, hogy az irracionális számok többen vannak, mint a racionálisok. Azt is tudjuk, hogy bármely két különböző irrac. szám között van legalább egy rac. szám és forditva.
Legyenek a,b Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c Q, vagyis rac szám úgy, hogy a<c<b. Ekkor létezik a', a' Q, vagyis rac szám úgy, hogy a<c<b. Ekkor létezik a', a' Q*, c<a'<b. Ekkor létezik c', c' Q*, c<a'<b. Ekkor létezik c', c' Q, a'<c'<b. Ekkor... Q, a'<c'<b. Ekkor...
Képezzünk ezekből a számokból párokat úgy, hogy az első szám rac., a második irrac. legyen: (0,b), (c,a), (c',a'),...! Úgy tünik, hogy akárhányszor egy új irrac. számot veszünk a régiek mellé, mindannyiszor kapunk egy új rac. számot is.
Ezekszerint mégis van bijektiv leképezés a két halmaz között?
|
|
| [1350] bily71 | 2010-09-20 17:03:25 |
 Eszembe jutott egy régebbi vitánk a Brun-állandóról. Továbbra is fenntartom, hogy amig nem tudjuk, hogy az ikerprimek száma véges-e, avagy végtelen, addig felesleges, sőt butaság vizsgálni a Brun-állandó racionális, vagy irracionális voltát. Egy sorozat összegéről csak akkor tételezetjük fel, hogy irracinális, ha már tudjuk, hogy az végtelen sok tagból áll.
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
| [1349] bily71 | 2010-09-20 16:49:38 |
 Mondjuk B első számjegye 1, a második 4, a harmadik 1,... vagyis B a  soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta. soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta.
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
|




 ' létezik, azaz az irracionálisba hajtó játékosnak van nyerő stratégiája. Két egyszerű módszere is van. Az egyik az, hogy választ egy irracionális számot, és annak a jegyeit írja be, függetlenül attól, mit tesz a másik. Egy másik módszer pedig az, hogy sorbarendezi a racionális számokat, és az n. lépésében arra figyel, hogy az n. racionális számot elkerülje. Persze mindkettőt meg lehet formalizálni az előző hsz-emben levő módon (
' létezik, azaz az irracionálisba hajtó játékosnak van nyerő stratégiája. Két egyszerű módszere is van. Az egyik az, hogy választ egy irracionális számot, és annak a jegyeit írja be, függetlenül attól, mit tesz a másik. Egy másik módszer pedig az, hogy sorbarendezi a racionális számokat, és az n. lépésében arra figyel, hogy az n. racionális számot elkerülje. Persze mindkettőt meg lehet formalizálni az előző hsz-emben levő módon (

 2/6, irrac. Ha csak az első n négyzetszám reciprok összegét képezzük, akkor rac. számot kapunk. A részösszegek sorozata
2/6, irrac. Ha csak az első n négyzetszám reciprok összegét képezzük, akkor rac. számot kapunk. A részösszegek sorozata 

 Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c
Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c