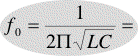| [146] fermel | 2007-02-17 15:06:02 |
 Mekkora az a legkisebb n, melyre biztosan igaz a következő? n db síkbeli rácspont esetén biztosan találunk köztük három olyat, amelyek által alkotott háromszög súlypontja is rácspont.
Köszönöm a segítséget. fermel
|
|
| [145] tim20 | 2007-02-16 13:01:02 |
 A könyvet sajnos nem tudom most beszerezni, de én azt mondom, hogy a második a nagyobb. Megerősítenél ha Te még a könyv oldalszámát is tudod? Előre is köszi.
|
| Előzmény: [144] jonas, 2007-02-16 12:09:19 |
|
|
| [143] tim20 | 2007-02-16 11:39:14 |
 Melyik a több? Fél tucat tucat tucat tucat, vagy hat tucat tucat tucat tucat? A második vagy az első vagy egyenlőek?
|
|
| [142] Lóczi Lajos | 2007-02-15 11:44:52 |
 Itthon a fuggvenyt inkabb Riemann-fuggvenynek hivjuk, a Dirichlet-fuggveny a racionalis szamok karakterisztikus fuggvenye (vagy annak "komplementere") szokott lenni.
|
| Előzmény: [141] jonas, 2007-02-14 23:12:49 |
|
|
| [140] nyida | 2007-02-14 22:13:33 |
 Helló! Kellene nekem kép, link, akármi arról a függvényről, amit Riemann talált ki, és az a szabály, hogy ha x irracionális, akkor a függvény 0, ha x racionális, akkor a függvény értékét a racionális szám közönséges törtalakjából a számláló 1-re cserélésével kapjuk. A függvényt 0 és 1 közt értelmezzük. Ez az első olyan függvény, ami minden racionális ponton szakad, minden irrac ponton folytonos. Kösz
|
|
| [139] Noémi | 2007-02-12 00:19:52 |
 Sziasztok! Éppen egy felejthetetlen kiselőadásra készülök, és véletlenül bukkantam erre az oldra. Így viszont kapva kapok eme páros , és soha vissza nem térő lehetőségen és a segítségeteket kérném. Én inkább (kb. 100%) humán beálítottságú vagyok, viszont, most a fősulin kéne tartanom egy előadást, melynek címe; elektromosság, mágnesesség. A tanárnő azt kérte, hogy mindenképpen CSAK érdekességeket említsek a témával kapcsolatban,(viszont az bármi lehet ami egy kicsit is kontektussal van e témával) és kerüljem az unalmas elméleti részt, melynek nagyon örültem, egészen addig amíg újfent rá nem jöttem, hogy értelmes ötleteknek még a halvány szikrája sem sziporkázik elmémben. Úgy gondoltam, miközben a fórum oldalain mozgattam szemgolyómat, hogy nektek biztos lennének jó ötleteitek eme fergeteges problémámra (remélem ennél nagyon soha nem lesz :) Én persze ha megadtok témát, annak utána nézek, s pótolom eme témával kapcsolatos hiányosságomat. Előre is köszönöm mindannyiotoknak; Noémi :)
|
|
| [137] thukaert | 2007-01-30 19:54:26 |
 A többváltozós diofantoszi egyenleteknél szükség van arra hogy megoldást rendezett n-es formájában adjuk meg, hiszen az hogy egy diofantoszi egyenletnek (2,1) megoldása az nem azt jelenti hogy az (1,2) is az.A sorrend itt a változók sorrendjét követi pl.: (x,y)=(2,1) ez pontosan azt jelenti hogy x=2 és y=1
vagy
(x,y,z)=(3,4,5) x=3 y=4 z=5
így (1,2) nem egyenlő (2,1)-el a rendezés tehát fontos,mert nem biztos hogy az egyenlet szimmetrikus a változóiban.
|
| Előzmény: [136] epsilon, 2007-01-30 13:08:45 |
|
| [136] epsilon | 2007-01-30 13:08:45 |
 Helló! Banális a kérdés, de, nem látom az értelmét, hogy egy adott diofantikus egyenlet egész megoldásainak keresésénél, miért teszik oda, hogy az (x,y) rendezett egész megoldásait kerseik? Mit kellene pluszban érteni a rendezés alatt, mint amit megszoktunk, hogy (x,y) nem ugyanaz mint (y,x), másvalamit? Vagy ezzel ki akarják zárni az (x,x) számpárokat?
|
|
|
|
| [133] waszlavikm | 2007-01-18 20:00:37 |
 Tisztelettel üdvözlök mindenkit!
51 éves vagyok, sajnos régen jártam iskolába. Kérem, ha valaki tud segítsen! Adott egy kör alakú kert. A kör kerületén, azaz a kert szélén, leverünk egy karót, melyhez kötéllel kikötünk egy éhes kecskét. Milyen hosszú legyen a madzag, hogy a kecske, a kert területének a felét legyen képes lelegelni?
Köszönettel: Waszlavik Miklós
|
|
| [132] ^mtk | 2007-01-18 19:26:54 |
 Koszonom!
Az alabbi kepletbol kellene szamitani L-t es C-t. Legyszi segitsetek..aztan egyelore ennyi volt:)
Koszonom!
|
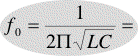 |
| Előzmény: [131] i, 2007-01-17 20:36:47 |
|
|
|
|
|
| [127] i | 2007-01-14 14:08:30 |
 Szívesen :)
|
|
|
| [125] i | 2007-01-14 12:58:20 |
 Az mindegy, csak a végén 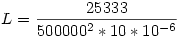 lesz. lesz.
Én az ilyesmit matekórán tanultam valamikor régen, egyenletrendezés címszóval lehetne esetleg rákeresni...
|
|
| [124] ^mtk | 2007-01-14 12:10:50 |
 Eredetileg a nevezoben kellene legyen a : 10*10 a -6.-on. Igy mar maskeppen fog festeni?
Amugy tudnal ajanlani valami anaygot hogy hol tudom ezeket megnezegetni/megtanulni?
Koszonom!
|
| Előzmény: [122] i, 2007-01-13 23:10:38 |
|
|
| [122] i | 2007-01-13 23:10:38 |
 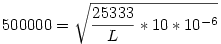
Ezt négyzetre emeled: 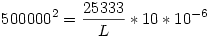
Beszorzol L-lel, és leosztasz 5000002-nel:
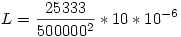
És már csak ki kell számolni :)
|
|
| [121] ^mtk | 2007-01-13 22:47:18 |
 Sziasztok!
En uj vagyok itt .. Nemi segitsegre lenne szuksegem,mivel nem ertem a matematikat,de igyekszem.
A kerdesem a kovetkezo lenne:
f = gyokalatt(n/L*C)
namost egy konkret esetre kellene megoldas.
500000 = gyokalatt(25333/L*10*10 a minusz 6.-on)
Itt L erteket kellene kiszamolni.
Legyszi irjatok le nekem hogy hogy kell,sorrol sorra,ok? Nem muszaly a megoldas csak az elv...( C-re is ugyanaz?)
Koszonom.
|
| Előzmény: [1] Brigi, 2005-08-26 19:45:29 |
|