|
| [1500] Zine | 2011-04-11 20:52:40 |
 Részben igaz a sejtés:) Két eset van, vagy az, amit te is leírsz, vagy pedig ha n = (k-1)k + 1, akkor felbontható n darab Kk-ra, például K7 felbontható 7 db háromszögre. Csak ebben a két esetben van egyenlőség.
Erdős-de Brujin-tétel a neve, ők tetszőleges pont-egyenes struktúrára fogalmazták meg, de a két megfogalmazás teljesen ekvivalens. Valamint a tétel onnan is ismerős lehet, hogy ennek egy speciális esete az az állítás, hogy n nem egy egyenesen lévő pont legalább n egyenest meghatároz. Sokszor ezt a tételt nevezik Erdős-de Brujin-tételnek az általánosabb helyett / mellett. (Persze egyből következik az is, hogy az általad sejtett eredmény ez utóbbi esetben már igaz is, mivel Gallai óta tudjuk, hogy van olyan egyenes, amely pontosan két pontot tartalmaz, vagyis a második konstrukció, amelyet említettem, a síkban nem valósítható meg, ha k legalább 2, míg gráfoknál akadálytalanul lehetséges)
Egyébként Graham-Pollak-tételt magát ismerem, de a bizonyítását nem tudom, úgyhogy majd töröm rajta én is fejem, és részemről igény biztos lesz a megoldásra, ha addig nem lesz meg. (amire elég nagy esélyt látok...)
|
| Előzmény: [1499] Maga Péter, 2011-04-09 22:43:27 |
|
| [1499] Maga Péter | 2011-04-09 22:43:27 |
 Köszönöm, de a Graham-Pollak-tételé az érdem... Ha egy teljes n csúcsú gráfot felbontunk teljes páros gráfok páronként éldiszjunkt uniójára (teljes páros gráf: két színosztály, köztük minden él be van húzva), akkor legalább n-1 páros gráfot kell használnunk. Akinek van kedve hozzá, az törje rajta a fejét, hogyan lehet ezt lineáris algebrai módszerrel bebizonyítani (eléggé hasonló ahhoz, amit én írtam erre a feladatra). Ha pár napig nem lesz rá megoldás, de van érdeklődés, akkor felírom én magam. Ami ott érdekes, hogy az n-1 sokféleképp előáll.
Ebben a feladatban én az n-re másféle konstrukciót nem látok, minthogy veszünk egy teljes n-1-est, és a plusz egy pontot összekötjük mindennel. Mindazonáltal az én megoldásomból nem látszik, hogy ez lenne az egyetlen megoldás. A tiedből (ami valóban sokkal egyszerűbb) sem látom így kapásból, ami nem jelent semmit (főleg a kapásból miatt:)). Persze az sem biztos, hogy igaz.
Egyébként korábban azt írtad, hogy ez egy ismert tétel. Van esetleg neve is? (Én a kombinatorikához elképesztően nem értek, de aki ismer, az ezt tudja is. Lehet, hogy már másnak is feltűnt...:))
|
| Előzmény: [1498] Zine, 2011-04-09 14:09:54 |
|
| [1498] Zine | 2011-04-09 14:09:54 |
 Ötletes megoldás:)
Egy másik általam ismert egy soros bizonyítása az állításnak: Kn = (E,V), |V| = n. Vegyünk egy v csúcsot, legyen rv azon klikkek száma, amelyek tartalmazzák. Egy L klikk csúcsainak számát, pedig jelöljük sL-lel. Tegyük fel, hogy n m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv sB, amiből következik: sB, amiből következik:
m(n-sB) m(m-rv) m(m-rv)
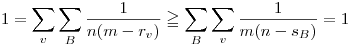
Ezzel, pedig kész is.
|
| Előzmény: [1487] Maga Péter, 2011-04-04 20:44:45 |
|
|
|
|
|
|
|
| [1491] KovácsPeti | 2011-04-05 16:58:53 |
 Hali! Nekem 1 kamatos kamattal kapcsolatos kérdésem lenne. Adott: Évi 82 különböző pénzösszeg: 20 000 Ft ; 2 000 000 Ft A kérdés pedig az, hogy melyik pénzösszeg duplázódik meg hamarabb, ha nem változik a kamat, illetve nem történik semmiféle tranzakció, tehát csak a kamatos kamat. Próbáltam beilleszteni a képletbe, de nem sikerült :(
|
|
|
| [1489] Alekszandrov | 2011-04-05 16:40:22 |
 Szia!
A baloldalt gyöktelenítsd és hozz közös nevezőre, majd a számlálóban előálló mértani közepek helyére írd be a számtani közepeket(természetesen ekkor jön be az ismert egyenlőtlenség). Ezután vonjál össze a számlálóban, egyszerűsíts és máris a jobboldalhoz érkeztél. Ebből már az is látszik, hogy egyenlőség csak a=b=c esetén lehetséges. Üdv!
|
| Előzmény: [1488] WhiteTiger94, 2011-04-05 15:55:15 |
|
| [1488] WhiteTiger94 | 2011-04-05 15:55:15 |
 Üdvözlet! Lenne önökhöz, hozzátok, egy kérdésem, rendezési tétel kellene hozzá ha jól sejtem, de a megoldásról nincs sejtésem, a feladatot elvileg ábraként csatolom a hozzászólásomhoz, és azt kellene megtudnom, mikor teljesül az egyenlőség, tehát, hogyha pl. a=b=c, vagy valamikor máskor?
Előre is köszönöm a segítséget.
Az ábra:
|
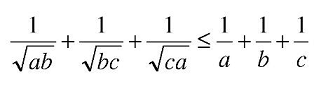 |
|
| [1487] Maga Péter | 2011-04-04 20:44:45 |
 Nem ismertem a tételt, de a Graham-Pollak-tétel lineáris algebrai bizonyítása megihletett:). Szóval tegyük fel, hogy az Ai klikkekre (1 i i m>1) felbontjuk a gráfot. Minden klikkhez rendeljük hozzá a m>1) felbontjuk a gráfot. Minden klikkhez rendeljük hozzá a  valós polinomot. Ekkor valós polinomot. Ekkor 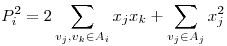 . Ha most feltesszük, hogy az Ai-k uniójában minden él pontosan egyszer szerepel, akkor . Ha most feltesszük, hogy az Ai-k uniójában minden él pontosan egyszer szerepel, akkor
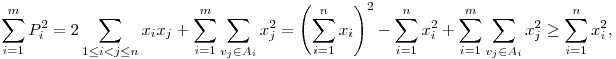
ahol az utolsó egyenlőtlenség azért áll fenn, mert a felbontás nemtriviális volt, amiből világos, hogy az eredeti gráf minden csúcsa legalább két Ai-ben szerepel.
Most indirekte tegyük fel, hogy m<n. Ekkor van nem azonosan 0 megoldása a P1=...=Pm=0 egyenletrendszernek (elemi lineáris algebra). Viszont akkor erre 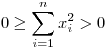 , ami ellentmondás. , ami ellentmondás.
|
| Előzmény: [1486] Zine, 2011-04-04 19:16:53 |
|
| [1486] Zine | 2011-04-04 19:16:53 |
 a) Igen, a Ramsey-tétel általánosítható uniform-hipergráfokra. Erről elég sok anyag van neten, pl wikipedia...
b) Ez egy viszonylag híres tétel, amelyet most szándékosan nem nevezek meg: Kn gráfot ha felbontjuk m Kn-től különböző klikkre, akkor m n n
|
| Előzmény: [1484] Radián, 2011-04-04 16:56:38 |
|
|
| [1484] Radián | 2011-04-04 16:56:38 |
 Hello!
Két kérdésem lenne az egyszerű gráfokkal kapcsolatban.
a.) Rendelkezünk-e bármiféle információval, hogy ha egy teljes gráf éleit akarjuk kiszínezgetni három színnel akkor minimum hány csúcs esetén fog egyszínű háromszöget v. négyszöget tartalmazni a gráfunk. (Van e Ramsey-számoknak valamilyen továbbfejlesztett alakja ?)
b.) Egy n csúcsú teljes gráfot felbontjuk 1-nél több ugyancsak teljes gráfra úgy hogy a kapott "kis" gráfok semelyikének se legyen közös éle. Mennyi kell legyen e "kis" gráfok minimális számossága ?
|
|
|
| [1482] psbalint | 2011-03-31 21:28:31 |
 köszönöm a segítséget. triviális feladatok között volt, és miután gondoltam/ajánlották a szitára/a szitát, én még mindig azt hittem, van valami teljesen nyilvánvaló megoldás, amit nem veszek észre.
|
|
| [1481] jonas | 2011-03-31 21:08:12 |
 Nem, ez így hibás, mert a mazsolák eloszlkása nem ugyanaz, mint a pálcikák eloszlása. Például ha két mazsolád és két süteményed lenne, akkor 1/4 valószínűséggel menne a bal oldali süteménybe mindkét mazsola, de 1/3 valószínűséggel menne mindkét mazsola a pálcáktól balra.
|
| Előzmény: [1479] psbalint, 2011-03-31 20:53:43 |
|
| [1480] jonas | 2011-03-31 21:05:56 |
 Feltételezem, hogy ezt úgy kell érteni, hogy ha a nagymama az egész tésztába rakott mazsolákat pontosan leszámolja, és biztosan ugyanannyit, n darabot rak.
Ha a tésztát tíz részre osztja, akkor minden mazsola egymástól függetlenül kerül a tíz rész valamelyikébe, és feltesszük azt is, hogy a tíz rész pontosan egyforma méretű, vagyis egyforma valószínűséggel kerülnek beléjük a mazsolák.
Most akkor ha kiválasztassz k konkrét süteményt, akkor annak a valószínűsége, hogy az összes mazsola ezekbe kerül, (k/10)n. Ebből azt hiszem, szitával következik, hogy annak a valószínűsége, hogy minden süteménybe kerül mazsola,

Ezt átalakítod 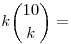  alapján, majd az összeget explicit alakra hozod, és innen próbáld meg te megoldani. alapján, majd az összeget explicit alakra hozod, és innen próbáld meg te megoldani.
|
| Előzmény: [1476] psbalint, 2011-03-31 14:24:15 |
|
| [1479] psbalint | 2011-03-31 20:53:43 |
 igen ez megvolt, de még mindig nem teljesen világos. lerakunk egy sorba n golyót, és lerakunk közéjük 9 pálcikát. és ahogy sorban rakosgatjuk a pálcikákat, mindig megnézzük, hogy mekkora valószínűséggel kerül olyan helyre (pl két pálcika egymás mellé), hogy az egy süteményre 0 mazsolát eredményezne. ez így megállja a helyét? most mondhatnám hogy azért csináltam golyókkal-pálcikákkal mert egy nem szakkörös gimisnek kell elmagyaráznom (egyébként így van), de igazából azért azért, mert nem tudtam kitalálni semmilyen matematikai képletes vagyis klasszikus megoldást.
|
|
|
| [1477] logarlécész | 2011-03-31 17:48:18 |
 Az első feladatban az egyenlet sinx-re másodfokú. Ha gondolod sinx-et jelölheted pl.: a-val. A-t beírva a sinx helyére egy sima másodfokú egyenletet kapunk.(öt a négyzet mínusz három a mínusz egy egyenlő nulla). Ezt gondolom meg tudod oldani. Lesz két megoldás, ebből jelen eseteben egy lesz mínusz egy és egy közötti. A színusz ÉK-e -1 - 1, tehát a másodfokú egyenlet egyik megoldásából (amelyik nem esik mínusz egy és egy közé) nem lesz megoldás, a másikból pedig teljesen egyszerűen sinx=a, amit gondolom szintén meg tudsz oldani. A második egyenletet átalakíthatod úgy, hogy 9sinx négyzet-(sinx négyzet+cosx négyzet)=8, ebből a négyzetes összefüggést használva (sinx négyzet+cosx négyzet=1)sinx=1, innen már gondolom megy. És most sajnos el kell mennem...
|
| Előzmény: [1475] Rozali, 2011-03-31 08:39:41 |
|




 m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv
m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv

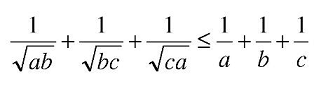
 i
i