|
|
| [1514] Zine | 2011-04-22 20:16:59 |
 Én láttam a feladatot, ezért nem is akartam először megnevezni a kérdezőnek, illetve többet mondani róla, viszont miután már feltöltötted a bizonyítását már lényegében mindegy volt.
Egyébként ilyenkor, ha valaki ismeri a tételt, akkor leírja a megoldásában hogy ez a tétel neve, hivatkozik egy bizonyításra, és kész? Vagy erre nem is adnának pontot?
|
| Előzmény: [1511] Maga Péter, 2011-04-22 15:11:23 |
|
| [1513] rizsesz | 2011-04-22 18:49:20 |
 Ez azért meglehetősen furcsa; szerintem talán az történhetett, hogy az elektronikusan beküldött megoldások értékét feltöltötték, a papír alapúakat pedig még nem (ilyen olykor megesik).
|
| Előzmény: [1512] Róbert Gida, 2011-04-22 17:32:24 |
|
|
|
|
|
|
|
|
| [1505] ga.bakonyi | 2011-04-19 16:35:26 |
 Szép napot mindenkinek,
lehet, hogy retorzió következik a hozzászólás miatt, de ha szépen megkérek valakit, aki tudja, megmondja nekem, milyen a Leontief-féle termelési függvény általános alakja és képlete? Nagyon szépen köszönöm.
|
|
| [1504] TiCoN314 | 2011-04-19 10:59:59 |
 Üdv!
Egy kis segítségre lenne szükségem: Ugye van egy tételünk, hogy ha egy vektor-valós fgv. esetén egy adott pontban minden parc. derivált létezik és folytonosak, akkor ott totálisan diff-ható. Legyen f(x,y)= 1, ha x*y=0, különben 0. Ez esetben az origóban a parciális deriváltak léteznek és folytonosak (0), mégsem differenciálható a függvény, hiszen nem is folytonos a (0,0)-ban. Hol a hiba?
Előre is köszönöm a segítséget.
Üdv: TiCoN
|
|
| [1503] Maga Péter | 2011-04-12 08:19:47 |
 Nahát, de ostoba vagyok, ezt a Fano-síkból adódó felbontást és rokonait igazán észrevehettem volna...
Ha már az egyenes-pont felállásnál tartunk, akkor arra is mutatok egy lineáris algebrai bizonyítást (n pont, nincs mind egy egyenesen, ekkor n egyenest meghatároznak).
Először egy feladat, amit Pósa Lajos táborában tanultam. Van n pont, nincs mind egy egyenesen, mindegyikre ráírunk egy valós számot úgy, hogy minden legalább 2 pontú egyenesen 0 az összeg. Ekkor minden pontra 0-t kell írnunk. A bizonyítás nem nehéz.
Most minden Ai pontra vegyük az xi valós polinomot. Minden legalább kétpontú e egyenesre legyen  . Az előbb leírtak szerint a 'Pe=0 minden e-re' egyenletrendszernek csak triviális megoldása van, így legalább n egyenletből áll. . Az előbb leírtak szerint a 'Pe=0 minden e-re' egyenletrendszernek csak triviális megoldása van, így legalább n egyenletből áll.
|
| Előzmény: [1500] Zine, 2011-04-11 20:52:40 |
|
|
|
| [1500] Zine | 2011-04-11 20:52:40 |
 Részben igaz a sejtés:) Két eset van, vagy az, amit te is leírsz, vagy pedig ha n = (k-1)k + 1, akkor felbontható n darab Kk-ra, például K7 felbontható 7 db háromszögre. Csak ebben a két esetben van egyenlőség.
Erdős-de Brujin-tétel a neve, ők tetszőleges pont-egyenes struktúrára fogalmazták meg, de a két megfogalmazás teljesen ekvivalens. Valamint a tétel onnan is ismerős lehet, hogy ennek egy speciális esete az az állítás, hogy n nem egy egyenesen lévő pont legalább n egyenest meghatároz. Sokszor ezt a tételt nevezik Erdős-de Brujin-tételnek az általánosabb helyett / mellett. (Persze egyből következik az is, hogy az általad sejtett eredmény ez utóbbi esetben már igaz is, mivel Gallai óta tudjuk, hogy van olyan egyenes, amely pontosan két pontot tartalmaz, vagyis a második konstrukció, amelyet említettem, a síkban nem valósítható meg, ha k legalább 2, míg gráfoknál akadálytalanul lehetséges)
Egyébként Graham-Pollak-tételt magát ismerem, de a bizonyítását nem tudom, úgyhogy majd töröm rajta én is fejem, és részemről igény biztos lesz a megoldásra, ha addig nem lesz meg. (amire elég nagy esélyt látok...)
|
| Előzmény: [1499] Maga Péter, 2011-04-09 22:43:27 |
|
| [1499] Maga Péter | 2011-04-09 22:43:27 |
 Köszönöm, de a Graham-Pollak-tételé az érdem... Ha egy teljes n csúcsú gráfot felbontunk teljes páros gráfok páronként éldiszjunkt uniójára (teljes páros gráf: két színosztály, köztük minden él be van húzva), akkor legalább n-1 páros gráfot kell használnunk. Akinek van kedve hozzá, az törje rajta a fejét, hogyan lehet ezt lineáris algebrai módszerrel bebizonyítani (eléggé hasonló ahhoz, amit én írtam erre a feladatra). Ha pár napig nem lesz rá megoldás, de van érdeklődés, akkor felírom én magam. Ami ott érdekes, hogy az n-1 sokféleképp előáll.
Ebben a feladatban én az n-re másféle konstrukciót nem látok, minthogy veszünk egy teljes n-1-est, és a plusz egy pontot összekötjük mindennel. Mindazonáltal az én megoldásomból nem látszik, hogy ez lenne az egyetlen megoldás. A tiedből (ami valóban sokkal egyszerűbb) sem látom így kapásból, ami nem jelent semmit (főleg a kapásból miatt:)). Persze az sem biztos, hogy igaz.
Egyébként korábban azt írtad, hogy ez egy ismert tétel. Van esetleg neve is? (Én a kombinatorikához elképesztően nem értek, de aki ismer, az ezt tudja is. Lehet, hogy már másnak is feltűnt...:))
|
| Előzmény: [1498] Zine, 2011-04-09 14:09:54 |
|
| [1498] Zine | 2011-04-09 14:09:54 |
 Ötletes megoldás:)
Egy másik általam ismert egy soros bizonyítása az állításnak: Kn = (E,V), |V| = n. Vegyünk egy v csúcsot, legyen rv azon klikkek száma, amelyek tartalmazzák. Egy L klikk csúcsainak számát, pedig jelöljük sL-lel. Tegyük fel, hogy n m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv sB, amiből következik: sB, amiből következik:
m(n-sB) m(m-rv) m(m-rv)
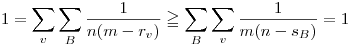
Ezzel, pedig kész is.
|
| Előzmény: [1487] Maga Péter, 2011-04-04 20:44:45 |
|
|
|
|
|
|
|








 m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv
m. B egy olyan klikk, amelynek nem csúcsa v. Ekkor fennáll, hogy rv