| [1576] bily71 | 2011-11-21 22:28:11 |
 Üdv!
Lenne egy kérdésem.
A pozitív racionális számok definíció szerint felírhatók két azonos előjelű egész hányadosaként. Az egyértelműség kedvéért vegyük csak azt az esetet, mikor mind a számláló, mind a nevező pozitív egész.
A számelmélet alaptétele szerint bármely egynél nagyobb pozitív egész, a sorrendtől eltekintve, egyértelműen bomlik prímszámok szorzatára. Ebből következik, hogy  n n N* felírható N* felírható 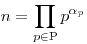 alakban, ahol P={prímek}, alakban, ahol P={prímek},  p p N és 0, vagy véges sok esetben igaz, hogy N és 0, vagy véges sok esetben igaz, hogy  p p 0. 0.
A fentiekből következik, hogy  q q Q+ felírható Q+ felírható 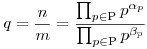 alakban, mely felírás egyértelmű, ahol n,m alakban, mely felírás egyértelmű, ahol n,m N*, (n,m)=1, N*, (n,m)=1,  p, p, p p N és 0, vagy véges sok esetben igaz, hogy N és 0, vagy véges sok esetben igaz, hogy  p, p, p p 0. 0.
Legyen (an,n N*) olyan sorozat, ahol ai N*) olyan sorozat, ahol ai Q+! Ekkor Q+! Ekkor 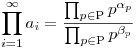 , mely alakot az egyszerűsítések elvégezte után kapunk. , mely alakot az egyszerűsítések elvégezte után kapunk.
A kérdésem:
Jól gondolom-e, hogy amennyiben az egyszerűsítések elvégezte után 0, vagy véges sok esetben igaz, hogy  p, p, p p 0, akkor 0, akkor 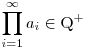 , különben , különben 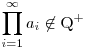 ? ?
Másik:
Jól gondolom-e, hogy ha létezik olyan prím, hogy a sorozat végtelen sok tagjára igaz, hogy a prím előfordul a nevezőben, de véges sok tagjára igaz, hogy előfordul a számlálóban, vagy fordítva, a sorozat végtelen sok tagjára igaz, hogy a prím előfordul a számlálóban, de véges sok tagjára igaz, hogy előfordul a nevezőben, akkor 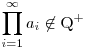 ? ?
|
|
|
| [1574] laci777 | 2011-10-17 15:45:56 |
 Sziasztok!
Ugyan most vesszük a deriválást, de egy feladat kifogott rajtam. Ha valaki tudna segíteni, megköszönném.
A példa: adott egy r sugarú gömb. Mekkora az ebbe a gömbbe szerkeszthető maximális térfogatú henger?
Bocs, ha túl egyszerű ez a pélfa, de bevallom kifog rajtam:(
Előre is köszönöm.
|
|
| [1573] Tóbi | 2011-10-15 18:16:03 |
 Legyen O egy pont a síkon. Legyen r az O távolságának maximuma az 5n adott objektumtól. Vegyünk egy O középpontú R sugarú kört. Ha R elég nagy, akkor belátjuk, hogy lesz rajta megfelelő P pont. A körvonal egy pontjának távolsága egy adott ponttól legalább R-r, ezen távolságok összege így legalább 2nR-2nr. Ha e egy adott egyenes, legyen e' a vele párhuzamos O-n átmenő egyenes. Ha p a körvonal egy pontja, akkor p és e távolsága legfeljebb annyi, mint p és e' távolsága plusz r. p és e' távolságának átlaga, miközben p fut a körön 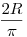 lesz, mivel ennyi a |sin(x)|R függvény átlagos nagysága is. Így összegezve a 3n egyenesre legfeljebb lesz, mivel ennyi a |sin(x)|R függvény átlagos nagysága is. Így összegezve a 3n egyenesre legfeljebb 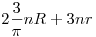 lesz az átlagos távolságösszeg. Ha R elég nagy, akkor lesz az átlagos távolságösszeg. Ha R elég nagy, akkor 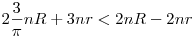 . Tehát valamely P pont jó lesz a körvonalon (például az, aminek minimális a távolságösszege az egyenesektől). . Tehát valamely P pont jó lesz a körvonalon (például az, aminek minimális a távolságösszege az egyenesektől).
|
| Előzmény: [1572] logarlécész, 2011-10-15 16:03:51 |
|
| [1572] logarlécész | 2011-10-15 16:03:51 |
 Adott a síkon 2n pont és 3n egyenes. Bizonyítsuk be, hogy van a síkon olyan P pont, hogy P-nek a 3n egyenestől való távolságainak összege kisebb, mint p-nek a 2n ponttól való távolságainak összege!
Eddig még n=1-re sem tudtam belátni.
Ha valaki tudna segíteni megköszönném. (Nem fontos és sürgős, csak érdekel.)
|
|
|
|
| [1569] phoenix | 2011-10-05 17:45:17 |
 Valamit én is gondoltam, de azt hittem átlátom amit írtam, de mégse ... lényegében az a) ill. b) feladatrész ugyanolyan elven működik ezek szerint, csak máshogy kell csoportosítani. Köszi a pontosítást vagy az érthetőbb megvilágítást :-) Köszi
|
| Előzmény: [1568] Sirpi, 2011-10-05 17:13:38 |
|
| [1568] Sirpi | 2011-10-05 17:13:38 |
 Uhh, belekavarodtam a skatulyáidba :-)
A lényeg, hogy 129 skatulyánk van (a prímek 129-es maradéka alapján), tehát valamelyik maradékból végtelen sok van, és erre a végtelen sok prímre igaz, hogy bármely kettő különbsége osztható 129-cel. Nyilván ez a bizonyítás tökéletesen működik bármilyen más számra is. Lényegében ezt írtad le Te is, csak túl sok volt a kérdőjel, és túl hosszúak a mondatok :-)
|
| Előzmény: [1567] phoenix, 2011-10-05 16:40:36 |
|
| [1567] phoenix | 2011-10-05 16:40:36 |
 Lemaradt a kérdőjel a végéről, de értelmesnek tűnhet? és ha azt kell bebizonyítani hogy végtelen sok prímszám van, melyek közül bármely kettőnek különbsége osztható 129-el? ügye itt is végtelen sok prímszámból válogatunk, de végtelen sokat abból is, mégpedig úgy hogy, mindegyik prímnek 129-el osztva ugyanolyan maradékot kell adnia. Erre is ugyanaz a skatulya-elv működhet? de az elsőnél véges sok skatulyába tettünk végtelen sok prímszámot, de itt véges skatulya van úgyszint, de nem csak egy elemre kell belátni, hanem hogy végtelen sok ilyen prímszámot tudunk kiválasztani, amik 129-el osztva azonos maradékot adnak.
|
|
| [1566] phoenix | 2011-10-05 16:32:45 |
 Az esetleg értelmesnek tűnhet, hogy tekintjük a 10 ad 10-en osztási maradékait, és ezeket tekintjük skatulyáknak, nyílván ezekből a skatulyákból véges sok van, ellenben azzal hogy végtelen sok prímszámunk van, és mindenképp lesz olyan két prímszám amit ha osztunk 10 ad 10-el, akkor ugyanannyi maradékot ad, és ezért különbségük osztható lesz vele.
|
| Előzmény: [1559] jonas, 2011-10-04 20:32:12 |
|
|
|
| [1563] phoenix | 2011-10-05 01:00:56 |
 Mondjuk lehetne olyan megoldás arra, hogy bebizonyítani hogy 10 ad 10 +3 prím, hogy ha p prím és c tetszőleges szám, akkor p | c ad p - c , de ez elég brute force technika
|
| Előzmény: [1559] jonas, 2011-10-04 20:32:12 |
|
|
|
|
|
|
| [1557] phoenix | 2011-10-04 20:07:02 |
 Jah, ezért gondoltam, hogyha be lehetne látni hogy mondjuk 10 ad 10 + 3 prím, akkor lehet ez az egyik szám, másik 3, de ez nem túl egyértelmű ... gondoltam skatulyára, de..
|
| Előzmény: [1556] phoenix, 2011-10-04 20:05:46 |
|
|
|
|
| [1553] phoenix | 2011-10-04 19:59:49 |
 Nem tudom bebizonyítani, hogy prím, mert ha be tudnám, akkor onnan triviális lenne .. de nem hiszem hogy ilyen úton kell elindulni, azt kell bebizonyítani hogy van két ilyen prím, és az volt a kérdésem, hogy a bizonyítás ebben a részfeladatban ha mondok kettő ilyet az elég? vagy
|
| Előzmény: [1552] jonas, 2011-10-04 19:29:41 |
|
| [1552] jonas | 2011-10-04 19:29:41 |
 Nem értem. Azt szeretnéd belátni, hogy van két olyan prímszám, aminek a különbsége pontosan 1010 ? Be tudod bizonyítani, hogy mondjuk a 1010+33 prímszám, de a 1010+13 nem az?
|
| Előzmény: [1551] phoenix, 2011-10-04 18:11:47 |
|



 n
n N* felírható
N* felírható  p
p 0.
0.  p
p




