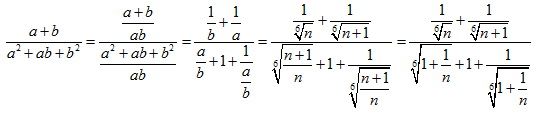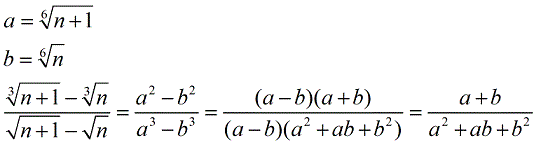Fórum: Valaki mondja meg!

- vagy az (5,7) -hez hasonló a (29.31) , vagyis 29+31=60 +/- 1 = 59/61 vagyis (59,61) ikerprím

- sok van még ilyen ?

- egy matematikai ikerprímekkel kapcsolatos feladat,kérdésem, a következő ,,véges vagy végtelen azon ikerprímek sora ,(mint pl. az 5,7) melyek összege plusz,mínusz egy ,kettő újabb,másik prímszámot generál,alkot ?"

- sőt kicsit tovább megyek és azt kérdezem : ,,véges vagy végtelen azon ikerprímek sora melyek összege plusz,mínusz egy, másik,újabb ikerprímet generál,alkot ?" - erre példa az (5,7) lásd. 5+7=12 +/- 1 = 11/13

- a válaszokat és a segítséget előre is köszönöm !

Üdvözlettel,Jhony !

Köszönöm szépen a választ ! --- nos a kettő közül,az egyikhez hasonló ez lenne ,,két prímszám összege plusz,minusz egy legalább egy ,de lehetséges,hogy kettő újabb prímszámot(számokat) generál(alkot)" .

Attól tartok, bármilyen óvatosan fogalmazol is, nemhogy manapság, de szerintem az utóbbi kétszáz évben szinte reménytelen, hogy érdekes vagy hasznos - mások által nem ismert és nem triviális - sejtése legyen valakinek, aki nem rendelkezik az érintett matematikai ágazat mély ismeretével. Itt a fórum támái között több helyen találsz utalást hasonló kérdésekre. Például Goldbach sejtés, ikerprím sejtés.

- megtudná-e mondani valaki mi a helyzet manapság ,ha valakinek van egy vagy kettő matematikai sejtése - már csak az a kérdés,hogy máig senki által nem említett sejtések-e és ...,hogy a matematika ,,világában" mennyire számítanak ,számítanának ,,érdekes",mondjuk ,,hasznos" sejtésnek - bizonyos szemszögből nézve ...

- a válaszokat,hozzászólásokat előre is köszönöm !

Tudtok ebben segíteni?

Egy cég kétféle terméket gyárt. A P(x; y) -3x(négyzet)-y(köb)+6xy profitot (millió forint) fejezi ki a termékek árainak függvényében (ezer forint). A termékek milyen egységára mellett maximális a profit és mennyi az értéke?

- nagyon szépen köszönöm !!!

Üdvözlettel , Jhony !

Az elején a és b nem tetszőlegesen választott számok, hanem a két rögzített páratlan prímből ( p és k ) adódó értékek . Később viszont "if n is greater or equal 3 so always will be a number a and b such that n=a + b + 1" . Önmagában persze igaz, hogy ha n3 , akkor van olyan a és b egész, hogy n=a + b + 1 , csak ezeket nem szabad összekeverni az elején definiált, k-hoz ill. p-hez tartozó a-val és b-vel.

- meg tudná mondani valaki hol van a hiba az alábbi bizonyításban --- ,ha van ??? --- és,hogy azt bizonyítja e helyesen amit gondoltam ,vagyis azt a bizonyos ,,sejtést" ?

1. subst. - let p and k , two prime numbers greater or equal 2,from the set of prime numbers, P, in the form : p=2a + 1 and k=2b + 1 , such that a and b are natural numbers,from the set of natural numbers N, - let m=2n ,m greater or equal 4,even number,from the set of natural numbers N and n grater or equal 2,natural number from set of natural numbers N, 2. concl. - every even integer greater than 2 can be expressed as the sum of two primes 3. prove:- by ,,reductio ad absurdum” * - step 0. for n=2 --- m=4 --- 4=2+2 ** - step 1. for - if n is greater or equal 3 so always will be a number a and b such that n=a + b + 1 - prove. 3=1+1+1 4=2+1+1 5=2 +2+1 ................ n=a+b+ 1 - so for n=k than k=a+b+1 - suppose that is true - for k+1=(a+b+1)+1=(k)+1=k+1 - so for k+1 is true - for n grater than 2 always will be a number a and b such that n =a+b+ 1 *** - step 2. - every even integer greater than 4 can be expressed as the sum of two primes m=p+k - prove by ,,reductio ad absurdum" - so than m is not equal p+k - so than 2n is not equal 2a+1+2b+1 - so than 2n is not equal 2a+2b+2 / divide both sides by 2 - so than n is not equal a+b+1 - so what is in contradiction with the proof from step 1. where n=a+b+1 was proved that is true - so than m=p+k is proved that is true so,, every even integer greater than 4 can be expressed as the sum of two primes” --- q.e.d.

- köszönöm szépen és bocsánat a zavarásért !

Helyesbítés: ...szerepét [1601]-ben... .

Az [1600]-ban szereplő kifejezés szerepét [1601] az ab kifejezés vette át (...). A következő levezetés végén kapott emeletes tört számlálója 0-hoz, nevezője pedig 3-hoz tart, ha n.

Ezért a keresett határérték 0.

Ezek után mit csinálunk? Rendezzük, vagy azt mondjuk, hogy ha n tart a végtelenbe, akkor kb. n=n+1 => a=b => a kifejezés: 2/3a a tart a végtelenbe => 2/3a->0

A második attól függetlenül, hogy kihozza a jó megoldást(?), inkább fizikus megoldásnak tűnik a kerekítgetéssel. :-)

Az igazi megoldási menetben beírjuk a kifejezéseket és rendezgetjük tovább?

A jövőnek: a feladat a következő.

Persze meg lehet oldani algebrai átalakítások nélkül is, geometriai úton. Rajzoljuk le egy négyzetrácsos lapra a téglalapot. Ekkor a területét a téglalapban lévő kis négyzetek száma adja, míg a kerületének mérőszáma = határon levő kis négyzetek + 4 (a sarkoknál 2-szer kell számolni, meg persze fel kell tenni, hogy a és b 1-nél nagyobbak), így ha a terület és kerület azonos, akkor a szigorúan belül levő (a határral nem érintkező) kis négyzetek száma pont 4 kell legyen, azaz 1*4-es vagy 2*2-es téglalapot alkotnak, azaz az eredeti téglalap 3*6-os vagy 4*4-es volt.

Igen, ez a szép megoldás, de "bambán" is megy. Fejezzük ki a-t ab=2a+2b-ből. 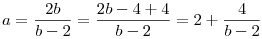Innen már adódik, hogy (b-2) csak 4 osztói közül kerülhet ki.

Alkalmazd az és az helyettesítéseket, ahol nyilván x>y>0 , majd a számlálót írd át így: . Egyszerűsítés után a számlálót és a nevezőt oszd el -nal, stb.

Egy jó félórát kínlódtam vele, hogy hogyan tudnám felhasználni a harmadik hatványra vonatkozó azonosságot harmadik gyökre, de nekem nem megy. Kaphatnék egy kis instrukciót?

A számlálót nem tudom gyökteleníteni, a nevező gyöktelenítésével pedig semmire nem jutok.

Nem írtál hülyeséget. Ezt az azonosságot - egy kis trükkel - igenis fel lehet használni ... :)

hülyeséget írtam, mert a feladatban köbgyök van

a³-b³=(a-b)(a²+ab+b²)

Gyöktelenítés.

Ehhez a feladathoz kérnék szépen segítséget: http://imageshack.us/photo/my-images/832/1gyak2d.png/ Előre is köszönöm!