Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[1746] Hölder	2012-04-23 17:42:18
Én is, de rengetegen használják a log-ot a fentiek ellenére, és őszintén megmondva ez engem zavar. Köszönöm, hogy válaszoltál a felvetett kérdésre.
Előzmény: [1745] Lóczi Lajos, 2012-04-22 23:24:08

[1745] Lóczi Lajos	2012-04-22 23:24:08
Nem a log-ot, hanem az ln-t, mert azt gyorsabban le lehet írni.
Előzmény: [1744] Hölder, 2012-04-22 18:30:38

[1744] Hölder	2012-04-22 18:30:38
Ezek szerint az log-t részesíted előnyben, ha jól értem?
Előzmény: [1743] Lóczi Lajos, 2012-04-20 12:25:37

[1743] Lóczi Lajos	2012-04-20 12:25:37
És figyelni kell a külföldi terminológiát is. Melyiknek van több létjogosultsága: "tan" vagy "tg"; "cot" vagy "ctg"; "rot" vagy "curl"; tizedespont vagy tizedesvessző; a szorzás jelölése ponttal vagy "x"-szel, a billió 10⁹ vagy 10¹²; a 7-es számjegy írása középen vízszintes áthúzással vagy anélkül?
Előzmény: [1742] Hölder, 2012-04-20 10:45:12

[1742] Hölder

2012-04-20 10:45:12

Sziasztok! Kinek mi a véleménye arról, hogy a természetes alapú logaritmust hogyan "kell" jelölni: ln vagy log? Kérlek írjátok meg, hogy szerintetek melyik a "helyes" és hogy miért gondoljátok úgy, hogy az a jó. Szerintem az ln-nek több létjogosultsága van, mert a természetes alapú logaritmus ugyebár logaritmus naturalis, innen jön az ln jelölés, aztán az egész középiskolai irodalom így jelöli, kivéve az egyetemeken, ott aztán mindkettő egyszerre él, attól függ melyik oktató óráján vagyunk (kb., mint hogy a 0 természetes szám -e). Aztán még egy indokot tudnék mondani így hirtelen: a komplex számok logaritmusát tényleg loggal jelöljük, ezzel megkülönböztetve a szokásos valós 8pontosabban pozitív9 számok logaritmusától, remélem mindenkinek ismert ez a jelölés,amiről beszélek. Lehet, hogy nem a legmegfelelőbb topikba írtam a kérdést, ezért elnézéseteket kérem, de jobb ötletem nem volt.

[1741] Lóczi Lajos

2012-04-12 00:46:03

A Taylor-sorokat pont erre találták ki, hogy az ilyen kifejezéseket racionális számokkal és alapműveletekkel lehessen felírni, azon az áron, hogy végtelen sok műveletet engedünk meg.

A példatárak gyakran azt értik a "pontos érték" alatt, hogy hozzuk a kifejezést "egyszerűbb" alakra, vagyis írjuk fel "elemibb" függvények segítségével -- bár ezt matematikailag pontosan sosem definiálják.

A mostani konkrét példabeli kifejezést egyszerűbb alakban nemigen lehet felírni.

Előzmény: [1740] kovátsnorbi1994, 2012-04-12 00:20:43

[1740] kovátsnorbi1994

2012-04-12 00:20:43

Mivel én többnyire csak a gimnáziumban elsajátítható ismeretekkel rendelkezem, és ott általában a pontosság fogalmát elintézik néhány mondattal, így számomra e kérdés nehéz. Mivel azonban ezt a kifejezést én is egy példatárból vettem, ezért tegyük fel, hogy amikor az előbbi kérdésem feltettem, én is azt értettem alatta, mint amire a könyv írója gondolt, amikor a feladathoz az említett megjegyzést fűzte.

Persze, ha ez a válasz nem elfogadható, elismerem, nem vagyok tisztában azzal, hogy mit jelenthet egy matematikához értő számára a "pontos érték" fogalom.

Nekem ez nagyjából annyit jelent, hogy a 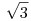$\sqrt{3}$ pontos értékét ugyan nem ismerem, de ha szükséges, megadott tizedesjegy pontossággal meg tudnám határozni a közelítő értékét, például úgy, hogy felülről, illetve alulról tetszőlegesen kicsi korlátok közé szorítom, miközben csak elemi műveleteket használok.

Ha a korábban leírt kifejezés alakját olyan alakúra lehetne hozni, amiben legfeljebb irracionális számok szerepelnek, valamint csak a négy elemi műveletet tartalmazza (kiegészítve a hatványozással és gyökvonással), akkor végeredményben ugyanígy - akár próbálgatással, ugyan hosszadalmas számolást követően, de írásban, segédeszköz használata nélkül - tetszőleges tizedesjegy pontossággal meg tudnám határozni a 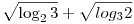$\sqrt{\log_2{3}}+\sqrt{log_3{2}}$ kifejezés nagyságát is.

Bár - belátom - ilyen módon tulajdonképpen a kívánt pontosságot a kifejezés jelenlegi formájában is el tudom érni, csak ez a számolás - a logaritmus jelenléte miatt - jóval több időt venne igénybe.

Előzmény: [1739] Lóczi Lajos, 2012-04-10 14:12:44

[1739] Lóczi Lajos	2012-04-10 14:12:44
Mit értesz pl. $\sqrt{3}$ pontos értékének meghatározása alatt?
Előzmény: [1738] kovátsnorbi1994, 2012-04-09 20:23:54

[1738] kovátsnorbi1994	2012-04-09 20:23:54
Tehát a $\sqrt{log_2{3}}+\sqrt{log_3{2}}$ kifejezés pontos értékének meghatározása érdekelne, amennyiben szerintetek lehetséges (mivel a leírt tévedés miatt ez végül - helyesen - nem került bele a példatárba ).
Előzmény: [1737] kovátsnorbi1994, 2012-04-09 20:15:15

[1737] kovátsnorbi1994

2012-04-09 20:15:15

Köszönöm a válaszokat azoknak, akik foglalkoztak vele!

Egyébként az említett kifejezés pontos értéke bármilyen egyéb módon megadható végülis?

Előzmény: [1736] sakkmath, 2012-04-08 16:25:51

[1736] sakkmath

2012-04-08 16:25:51

Megnéztem a könyvben a faladatot. A szerző a 86 - 88. oldalakon öt megjegyzést fűz a megoldáshoz. Az 1. megjegyzése még jó, a többi hibás! Például a 2. megjegyzés hibája ez: "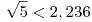 $\sqrt5 < 2,236$ ".

Scharnitzky a 3. megjegyzésben elkövetett súlyos hibát a 4. és 5. sorszámúakban még tovább is ragozta.

Előzmény: [1731] kovátsnorbi1994, 2012-04-07 21:30:34

[1735] Róbert Gida	2012-04-08 12:05:57
Nevezőben a zárójelben természetesen $\frac 12$ van.
Előzmény: [1734] Róbert Gida, 2012-04-08 11:51:50

[1734] Róbert Gida

2012-04-08 11:51:50

De ez például már igaz: 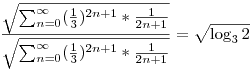$\frac {\sqrt {\sum _{n=0}^{\infty} (\frac {1}{3})^{2n+1}*\frac {1}{2n+1}}} {\sqrt {\sum _{n=0}^{\infty} (\frac {1}{3})^{2n+1}*\frac {1}{2n+1}}}=\sqrt {\log _3 2}$

"Nem értem, hogy az egyenlőség két oldalán lévő érték hogyan lesz egyenlő, vagyis miért emelhető-e szumma jel elé az összegzési indexet is tartalmazó hányados, ha véges sok esetben nincs egyenlőség a jobb- és baloldal között."

Egy mondatban ennyi zöldséget rég olvastam.

Előzmény: [1731] kovátsnorbi1994, 2012-04-07 21:30:34

[1733] Róbert Gida	2012-04-08 11:30:30
A hozzászólásban egy darab egyenlőtlenség sem szerepel.
Előzmény: [1732] Fálesz Mihály, 2012-04-08 05:32:40

[1732] Fálesz Mihály	2012-04-08 05:32:40
A szóbanforgó egyenlőtlenség nem igaz.
Előzmény: [1731] kovátsnorbi1994, 2012-04-07 21:30:34

[1731] kovátsnorbi1994

2012-04-07 21:30:34

Jó estét minden Fórumozónak!

A segítségetekre lenne szükségem egy példatárban olvasott megjegyzés értelmezésével kapcsolatban: A megjegyzéshez kapcsolódó feladat az /1989-1992/-es Egyetemi Felvételi Feladatok (Scharnitzky-féle) példatár 87. oldalán olvasható, ahol konvergens Taylor-sorral adnak felső becslést $\sqrt{log_2{3}}+\sqrt{log_3{2}}$ értékére. Itt leírják a következő átalakítást, ami nem világos számomra :

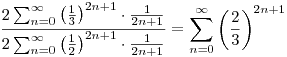
$\frac{2\sum_{n=0}^\infty \left(\frac13\right) ^{2n+1}\cdot{\frac1{2n+1}}}{2\sum_{n=0}^\infty \left(\frac12\right) ^{2n+1}\cdot{\frac1{2n+1}}}=\sum_{n=0}^\infty \left(\frac23\right)^{2n+1}$

Megnéztem konkrét, véges sok esetre az átalakítást: A baloldali összeg kifejtésére (véges sok esetben) a következőt kaptam:

$\frac{2\cdot\sum_{n=0}^3\left(\frac13\right) ^{2n+1}\cdot{\frac1{2n+1}}}{2\cdot\sum_{n=0}^3\left(\frac12\right) ^{2n+1}\cdot{\frac1{2n+1}}}=\frac{2\cdot[\left(\frac13\right)+\left(\frac13\right)^3\cdot \left(\frac13\right)+\left(\frac13\right)^5\cdot \left(\frac15\right)+\left(\frac13\right)^7\cdot \left(\frac17\right)]}{2\cdot[\left(\frac12\right)+\left(\frac12\right)^3\cdot \left(\frac13\right)+\left(\frac12\right)^5\cdot \left(\frac15\right)+\left(\frac12\right)^7\cdot \left(\frac17\right)]}$

Míg a jobboldali szumma kifejtésére:

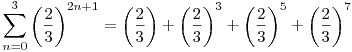
$\sum_{n=0}^3 \left(\frac23\right)^{2n+1}=\left(\frac23\right)+\left(\frac23\right)^3+\left(\frac23\right)^5+\left(\frac23\right)^7$

Nem értem, hogy az egyenlőség két oldalán lévő érték hogyan lesz egyenlő, vagyis miért emelhető-e szumma jel elé az összegzési indexet is tartalmazó 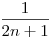$\frac{1}{2n+1}$ hányados, ha véges sok esetben nincs egyenlőség a jobb- és baloldal között.

A választ köszönöm, és békés ünnepeket kívánok mindenkinek!

[1730] kler69	2012-03-25 17:14:21
Nagyon szépen köszönöm! :)
Előzmény: [1729] jenei.attila, 2012-03-25 17:06:28

[1729] jenei.attila	2012-03-25 17:06:28
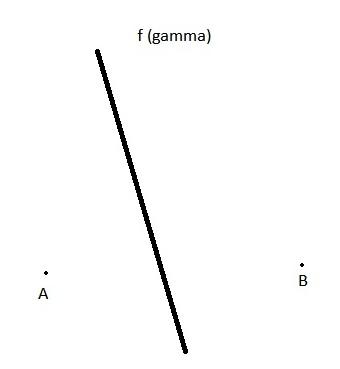
Mivel az f szögfelező, ezért az A pont f-re vett A' tükörképe rajta van a CB egyenesen. Tehát tükrözd A-t f-re (A'-őt kapod), majd az A'B és f egyenes metszéspontja megadja a C csúcsot.
Előzmény: [1728] kler69, 2012-03-25 16:52:41

[1728] kler69	2012-03-25 16:52:41
Kedves Mindenki! Sajnos már régen voltam iskolás, és a fiam ált. iskolás matekházija kifogott rajtunk. Kérem, aki tud, segítsen! A feladat: Adott egy háromszög A és B csúcsa, valamint a harmadik csúcsban levő szög szögfelezője. Szerkesszük meg a háromszöget! Köszönöm szépen!

[1727] Hölder	2012-03-25 12:12:25
Ez nagyon t5etszik, esetleg még a g(t) függvény konkáv voltára egy elemi bizonyítás, és akkor minden elemi benne. A többi felmerülő kérdésre is megpróbálok majd reagálni.
Előzmény: [1725] Fálesz Mihály, 2012-03-23 16:32:36

[1726] PAL	2012-03-23 16:38:15
Ha itt tudjuk a minimumot , akkor vehetnénk ugyanígy 2^-sin (x)+2^-cos (x) minimumát is, és éppen ott lenne maximuma a szóban forgó függvénynek, vagy tévedek?
Előzmény: [1724] Fálesz Mihály, 2012-03-23 10:45:42

[1725] Fálesz Mihály

2012-03-23 16:32:36

Én inkább a 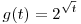$g(t)=2^{\sqrt{t}}$ függvényt vizsgálnám. A második derivált mutatja, hogy g a $[0,1]\subset\Big[0,\frac1{(\ln2)^2}\Big]$ intervallumban konkáv:

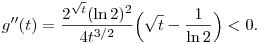
$g''(t) = \frac{2^{\sqrt{t}}(\ln2)^2}{4t^{3/2}}\Big(\sqrt{t}-\frac1{\ln2}\Big)<0.$

Ezért hát a Jensen-egyenlőtlenséget a g függvényre és az sin²x, cos²x pontokra felírva,

2^sin x+2^cos x $\le$ 2^|sin x|+2^|cos x|=g(sin²x)+g(cos²x) $\le$

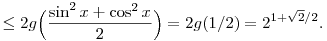
$\le 2 g\Big(\frac{\sin^2x+\cos^2x}2\Big) = 2 g(1/2) = 2^{1+\sqrt2/2}.$

Előzmény: [1722] spongya, 2012-03-22 23:24:12

[1724] Fálesz Mihály

2012-03-23 10:45:42

A minimum egyszerűen kijön a számtani-mértani közepekből és a $|\sin x+\cos x|\le\sqrt2$ egyenlőtlenségből.

$2^{\sin x}+2^{\cos x} \ge 2\sqrt{2^{\sin x}\cdot2^{\cos x}} \ge 2^{1-\sqrt2/2}.$

Előzmény: [1718] Lóczi Lajos, 2012-03-21 21:33:58

[1723] TLevi	2012-03-23 10:31:49
Igen...megneztem az [1705]-ot, de meg jobban kodben talaltam magam...
Előzmény: [1712] SmallPotato, 2012-03-19 08:54:53

[1722] spongya

2012-03-22 23:24:12

"Ha sikerülne elemi eszközökkel belátni, hogy 2^sin(x) alulról konkáv, ..."

Nekem + az jött ki, hogy $[0;\frac13]$ -ban 2^sin(x) alulról konvex. Sőt, a konvexitási tartomány jobbra még kicsit szélesíthető is. Vagy rosszul látom?

Előzmény: [1720] HoA, 2012-03-22 20:05:27

Már regisztráltál?
Új vendég vagy?