| [174] Sirpi | 2007-03-21 22:41:45 |
 Jól érzed :-)
Vegyünk pithagoraszi számhármasokat, pl:
32+42=52
122+52=132
202+212=292
Az elsőt beszorozva (13.29)2-nel kapjuk, hogy
(3.13.29)2+(4.13.29)2=(5.13.29)2
Ugyanígy a 2.-at és a 3.-at is megfelelően megszorozva:
(12.5.29)2+(5.5.29)2=(5.13.29)2
(20.5.13)2+(21.5.13)2=(5.13.29)2
És ez a módszer tetszőlegesen kiterjeszthető (mivel végtelen sok különböző pithagoraszi számhármas van), és mint látható, a jobb oldalakon mindig ugyanaz a szám áll.
|
| Előzmény: [173] Borgi - Tóth Áron, 2007-03-21 22:05:13 |
|
| [173] Borgi - Tóth Áron | 2007-03-21 22:05:13 |
 na, találtam egyet, ileltve hát kettőt 16 63, 65; 33 53, 65
ebböl arra merek következtetni hogy létezik sok ilyen pár, és létezik olyan x szám amihez n db, iylen pár tartozik.
|
|
| [172] Borgi - Tóth Áron | 2007-03-21 20:58:25 |
 sziasztok. remélem jó helyre írom a kérdésem.
lehet hogy a válasz már egyértelmű dolog, de én nem tudom, ezért bátorkodom megkérdezni
van-e olyan négyzetszám, ami több mint 1 négyzetszámösszeg párból előállitható?!
tehát
a2 + b2 = c2
és a,b,c egész számok. létezik-e olyan c, amihez több a és b pár tartozik?
|
|
| [171] fermel | 2007-03-17 20:27:28 |
 Ismét egy kombinatorikai feladat megoldásában szeretnék segítséget kérni. 13-as totóról van szó. Ebből 6 kimenetele egyértelmű, a további 7 pedig kétesélyes. Hány "szelvényt" kell legkevesebb kitölteni ahhoz, hogy biztosan legyen 12 találat? Adjuk is meg azokat a kitöltéseket, amelyek ezt biztosítják!
Odáig eljutottam, hogy 16 szelvény kitöltése elegendő. Viszont elképzelésem sincs arról, hogy milyen szisztéma szerint "töltsem ki a 16 szelvényt", hogy biztosan legyen 12 találat. (Végül is 7 kétesélyesből kell hatot biztosan eltalálni)
Köszönöm a segítséget: fermel
|
|
| [170] Lóczi Lajos | 2007-03-08 14:53:08 |
 Nézd meg pl. a Sárközy-Surányi: Számelméletfeladat-gyűjteményt, illetve annak függelékét. (Teljes bizonyításokat nem fogsz találni mindkettőre, de sok útmutatást igen.)
|
| Előzmény: [169] S.Ákos, 2007-03-07 20:14:06 |
|
| [169] S.Ákos | 2007-03-07 20:14:06 |
 Sziasztok!
Meg tudnáktok mondani, hogy hol lehet arra bizonyítást találni, hogy
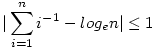
illetve

mindig mindig teljesül(pi az i-edik prímszám)?
|
|
|
|
|
| [165] Doom | 2007-03-05 18:50:45 |
 Egy 'a' oldalú szabályos háromszög minden csúcsában 1-1 kutya áll (A, B és C), majd egyszerre elkezdenek futni egymás felé azonos sebességgel: A B felé, B C felé és C pedig A irányában. Mennyi idő múlva találkoznak?
Segítségként egy "sejtés": egy furcsa "spirál-alakot" megtéve a háromszög középpontjában fognak találkozni, mégpedig egyszerre.
|
|
| [164] Lóczi Lajos | 2007-03-01 01:10:21 |
 Legyen tehát A>0 rögzített valós szám.
Pontos n értéket nem tudok mondani (szerintem általános A esetén nem is lehet (egykönnyen)), de legfeljebb 1 hibával meg tudom mondani a legnagyobb olyan n pozitív egész számot, amelyre nn/(n-1)n-1 legfeljebb A.
Nyilván csak az n>1 eset az érdekes, de ekkor A 4. Tegyük fel tehát a továbbiakban, hogy A>e. 4. Tegyük fel tehát a továbbiakban, hogy A>e.
A logaritmus sorfejtésével játszadozva be lehet látni például, hogy n 2 esetén fennáll az 2 esetén fennáll az
ne-e/2 nn/(n-1)n-1 nn/(n-1)n-1 ne-e/2-e/(4n) ne-e/2-e/(4n)
egyenlőtlenség. (Itt a két szélső kifejezés távolságát tetszőlegesen kicsivé össze lehetne húzni, de az nem segítene jobban.)
Innen most már csak elemi legfeljebb másodfokú egyenlőtlenségekkel (és a négyzetgyök sorfejtésével) továbbhaladva kapjuk, hogy
-- ha n<1/2+A/e, akkor A>nn/(n-1)n-1, az ilyen n-ek tehát még biztosan jók,
-- míg ha n>1/2+A/e+5e/(16A), akkor A<nn/(n-1)n-1, az ilyen n-ek tehát már biztosan rosszak.
Nem tudom eldönteni a kérdést, ha történetesen esik egész szám az [1/2+A/e,1/2+A/e+5e/(16A)] intervallumba (itt is ugyanaz a helyzet: ez az intervallum tetszőlegesen szűk, de fix hosszú lehetne); innen jön az, hogy ha nem is a legnagyobb, de legrosszabb esetben a második legnagyobb n-et tudom csak megadni.
|
| Előzmény: [160] S.Ákos, 2007-02-28 18:57:12 |
|
|
|
| [161] epsilon | 2007-02-28 19:26:43 |
 Hali! Szerintem nem létezik egy legnagyobb A mert a jobboldal bármilyen nagy lehet, ugyanis a jobboldali kifejezés így írható (n/n-1) az (n-1)-ik hatványon, × n, és az első tag az "1/e" számhoz tart, amikor n a végtelenhez tart, és a második tényező, az "n" tetszőlegesen nagy, amikor n a végtelenhez tart, tehát A minden korlátnál nagyobb lehet. Magyarán mondva a jobboildali tagból alkotott általános tagú sorozat korlátlan.
|
|
| [160] S.Ákos | 2007-02-28 18:57:12 |
 Sziasztok!
Vki meg tudná mondani, hogy hogy lehetne meghatározni azt a legnagyobb egészet, melyre
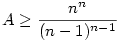
teljesül?(A egy tetszőleges poz. valós szám)
|
|
|
|
| [157] ScarMan | 2007-02-27 14:23:25 |
 Ha definiálunk egy új változót vagy függvényt vagy akármit, akkor az egyenlőségjel melyik oldalára kell írni a kettőspontot? Az új változó felől vagy a másik oldalra?
|
|
| [156] fermel | 2007-02-25 19:03:27 |
 Most már teljesen világos. Bár én a cserék alkalmazását kihagyom, de az indoklásom ugyanazokon az alapokon nyugszik. Nagyon sokat segítettél, köszönöm szépen. fermel
|
| Előzmény: [155] Sirpi, 2007-02-25 16:34:00 |
|
| [155] Sirpi | 2007-02-25 16:34:00 |
 Szóval felteszem, hogy le lehet tenni 5 pontot úgy, hogy ne keletkezzen rossz hármas. Ekkor nem lehet semelyik sorban 3 pont, mert akkor azok súlypontja a középső, így csak 2-2-1 lehet a megoszlás (nem feltétlen ebben a sorrendben), és ugyanez az oszlopokra is.
Azt állítom, hogy ha nincs rossz 3-as, akkor 2 sort megcserélve sem fog rossz 3-as keletkezni. Rossz 3-as csak úgy jöhet létre, hogy minden sorból és minden oszlopból egy elemet választok ki, hiszen egyik sor és oszlop sincs tele, az meg nem lehet, hogy 2-t az egyik sorból és 1-et egy másikból. Ilyenkor viszont a csere változatlanul hagyja az x- és y- koordináták összegét is, vagyis ha nem volt rossz hármas, akkor nem is jött létre új a csere hatására. Vagyis innentől szabadon csereberélhetem a sorokat és oszlopokat.
1. csere: a legfelső sorba viszek egy "dupla" (azaz 2 kiválasztott elemet tartalmazó) sort
2. csere: ebben a sorban a 2 elemet az első két helyre teszem
3. csere: felviszem a 2. sorba a másik dupla sort
4. csere: mivel az első 2 sorban 4 elem van, de csak 3 hely, ezért valahol egyeznek. Ezt az egyezést oszlopcserével az első oszlopba viszem
És ahogy már mondtam, most a (0,0) (1,0) (0,1) elemek ki vannak választva, és két eset van aszerint, hogy a 2. sorban melyik a másik kiválasztott elem. Innen úgy fejeződik be a bizonyítás, ahogy már leírtam.
|
| Előzmény: [154] fermel, 2007-02-25 16:14:08 |
|
| [154] fermel | 2007-02-25 16:14:08 |
 Pontosan eddig a segédállításig jutottam el én is és ennek a bizonyításánál akadtam el. A te bizonyításodból még sajnos az nem világos számomra, hogy miért csak az 1. és 2. eset jöhet szóba az első 4 pont vonatkozásában.( nem igazán értem a cseréket) Kifejtenéd kicsit bővebben? A bizonyítás többi része teljesen világos. Köszönöm. fermel
|
| Előzmény: [153] Sirpi, 2007-02-25 15:25:40 |
|
| [153] Sirpi | 2007-02-25 15:25:40 |
 8 nyilván nem elég (elég a koordináták 3-as maradékait kiírni):
(0; 0) (0; 0) (0; 1) (0; 1) (1; 0) (1; 0) (1; 1) (1; 1)
Itt csak úgy lehetne a súlypont rácspont, ha a négyzet valamelyik csúcsába esne, de akkor azt a csúcsot háromszor kellene kiválasztanunk, de mindegyik csak kétszer szerepel.
* * *
Ezek után be kellene látni, hogy 9 pontból viszont mindig kiválasztható a megfelelő 3.
Ennek belátásához egy segédállítás: a {0,1,2}×{0,1,2} halmaz 5 különböző elemét kiválasztva biztosan lesz köztük három, aminek súlypontja rácspont.
Ez azért van így, mert ha valamelyik sorban ki van választva 3 elem is, akkor készen vagyunk, ellenkező esetben viszont 2-2-1 a sorokban a kiválasztott elemek megoszlása, és ugyanez igaz az oszlopokra is. Veszem az első "dupla" sort és megcserélem az elsővel, majd oszlopcserékkel elérem, hogy a két elem az első 2 legyen a sorban. Ezután felviszem a 2. sorba a másik "dupla" sort, ennek valamelyik eleme felett is van elem, ezt az oszlopot megcserélem az első oszloppal. Innen két eset lehet az első két sor tekintetében:
1) a 4 pont egy négyzetet alkot a (0,0) (1,0) (0,1) (1,1) pontok által
2) a (0,0) (1,0) (0,1) (2,1) pontok vannak az első két sorban
Mindkét esetben nyilvánvaló, hogy a 3. sorban bármelyik elemet is választjuk ehhez a 4-hez, az létre fog hozni egy "rossz" ponthármast. Ezzel a segédállítást beláttuk.
Innen pedig készen vagyunk, mert maximum 4 különböző pontot választhatunk ki, mindegyiket legfeljebb kétszer (ha 3-szor választanánk, akkor az adott megháromszorozott pont önmagában meg fog felelni), ami összesen 8 pont legfeljebb.
Így beláttuk, hogy 9 pont kell legalább, hogy garantáltan kiválasztható legyen közülük 3 úgy, hogy azok súlypontja is rácspont.
|
| Előzmény: [152] fermel, 2007-02-25 12:46:22 |
|
| [152] fermel | 2007-02-25 12:46:22 |
 Valóban igaz,hogy nem is biztos, hogy létrejön háromszög. A feladatot akkor átfogalmazva: Hány rácspont elegendő, hogy biztosan találjak három olyat,hogy a megfelelő koordináták összege biztosan osztható legyen hárommal? Igazából egy kombinatorikai feladatot helyeztek geometriai csomagolásba, a lényeg számomra a kombinatorikai rész megoldása lenne. Most éppen ott tartok, hogy a válasz valószínűleg 9, de a bizonyítással gondjaim vannak. fermel
|
| Előzmény: [151] S.Ákos, 2007-02-23 19:22:32 |
|
|
|







 4. Tegyük fel tehát a továbbiakban, hogy A>e.
4. Tegyük fel tehát a továbbiakban, hogy A>e. 

