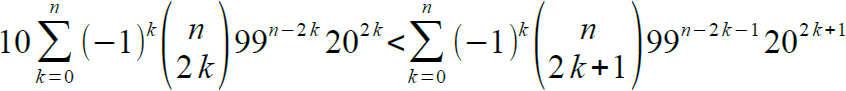Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[1809] Lóczi Lajos	2012-11-28 01:05:12
Amúgy milyen rendszerben milyen ütközéseket modellez ez az egyenlőtlenség?
Előzmény: [1806] polarka, 2012-11-28 00:32:00

[1808] polarka	2012-11-28 00:33:50
8-as van. ComplexExpand-dal működött.
Előzmény: [1805] Róbert Gida, 2012-11-26 23:28:22

[1807] polarka	2012-11-28 00:32:58
így már ezt is értem, köszi.
Előzmény: [1802] Lóczi Lajos, 2012-11-26 16:21:35

[1806] polarka

2012-11-28 00:32:00

Akkor a reláció iránya változna és n értékére maximumot kapnánk. Ami viszont az alap (fizikai) példát tekintve nem volna értelmes.

n jelöli azon ütközésszámot, amitől kezdve több ütközés nem lehetséges, értéke min 1.

Viszont belátom, hogy megéri az 1787. hozzászólásod 3. egyenlőtlensége szerinti cos-ra átalakítás.

Előzmény: [1800] Lóczi Lajos, 2012-11-26 14:35:17

[1805] Róbert Gida	2012-11-26 23:28:22
Segítsél Wolframnak egy kicsit: k menjen $\frac {n-1}2$ -ig, illetve $\frac n{2}$ -ig. De az is lehet, hogy más mathematica a verziód, és ezért nem hozta ki ezt az alakot.
Előzmény: [1791] polarka, 2012-11-25 17:15:38

[1804] Lóczi Lajos	2012-11-26 22:51:04
Köszönöm.
Előzmény: [1803] Moderátor, 2012-11-26 22:37:26

[1803] Moderátor	2012-11-26 22:37:26
A linkből hiányzott a "http://".
Előzmény: [1801] Lóczi Lajos, 2012-11-26 16:25:05

[1801] Lóczi Lajos

2012-11-26 16:25:05

Vmiért a Fórum belerakta az előbbi linkbe előtagként saját magát, tehát a link újra:

www2.math.ou.edu/~jalbert/putnam/putnam9.pdf

Előzmény: [1802] Lóczi Lajos, 2012-11-26 16:21:35

[1802] Lóczi Lajos	2012-11-26 16:21:35
Itt részletesebben ki van fejtve a gondolat.
Előzmény: [1799] polarka, 2012-11-26 14:11:43

[1800] Lóczi Lajos	2012-11-26 14:35:17
De nem csak a 0-val osztás lehet gond, hanem ha a koszinusz negatív, amivel az egyenlőtlenséget elosztod, ezek mind külön meggondolásokat igényelnek.
Előzmény: [1798] polarka, 2012-11-26 13:59:40

[1799] polarka

2012-11-26 14:11:43

Viszont én ezt nem tudom végigkövetni:

"tn(2cos t)=2cos (nt)" -nak mi köze az utána felírt u+1/u polinomhoz?

"Ebből azonnal következik..." Nem látom, hogy hogyan.

Előzmény: [1797] Fálesz Mihály, 2012-11-26 06:52:29

[1798] polarka

2012-11-26 13:59:40

Ha nem is bizonyítjuk be, akkor még utólag leellenőrizhetjük, hogy a kapott n-nel ellentmondásra jutunk-e.

$cos \left(n \cdot {\rm arctg} \frac{20}{99}\right)=0 ?$

Előzmény: [1796] Lóczi Lajos, 2012-11-26 00:11:36

[1797] Fálesz Mihály

2012-11-26 06:52:29

Nem olyan hosszú a bizonyítás.

(A Csebisev-polinomok helyett) azt a t_n(x) polinomot érdemes vizsgálni, amire t_n(2cos t)=2cos (nt) avagy $t_n\left(u+\frac1u\right)=u^n+\frac1{u^n}$ . Ez egy egész együtthatós polinom, a főegyütthatója 1, tehát a t_n(x)=k alakú egyenletek (k egész) minden racionális gyöke egész.

Ebből azonnal következik, hogy ha x/ $\pi$ és cos x is racionális, akkor 2cos x értéke 0, $\pm$ 1 vagy $\pm$ 2.

A tangensre például a $\cos x=\frac{1-\tg^2\frac{x}2}{1+\tg^2\frac{x}2}$ azonossággal térhetünk át.

Előzmény: [1796] Lóczi Lajos, 2012-11-26 00:11:36

[1796] Lóczi Lajos	2012-11-26 00:11:36
Viszont úgy gondolom, hogy mi nem tudjuk bebizonyítani, hogy $\frac{1}{\pi}{\rm{arctg}\frac{20}{99}}$ irracionális.
Előzmény: [1794] polarka, 2012-11-25 23:37:25

[1795] polarka	2012-11-25 23:42:51
Köszi.
Előzmény: [1793] Lóczi Lajos, 2012-11-25 20:14:53

[1794] polarka	2012-11-25 23:37:25
Arra gondoltam, hogy $\frac{1}{\pi} {\rm arctg}\frac{20}{99}$ továbbra is irrac. és mivel n természetes, így $n \cdot {\rm arctg}\frac{20}{99}$ szorzatuk sosem lesz $\frac{\pi}{2}$ többszöröse.
Előzmény: [1792] Lóczi Lajos, 2012-11-25 20:09:33

[1793] Lóczi Lajos	2012-11-25 20:14:53
Próbáld a ComplexExpand paranccsal.
Előzmény: [1791] polarka, 2012-11-25 17:15:38

[1792] Lóczi Lajos	2012-11-25 20:09:33
És a koszinusszal való átosztáskor hogyan garantálod, hogy ne legyen 0 a nevező? (És egyenlet nem, csak egyenlőtlenség szerepel:)
Előzmény: [1790] polarka, 2012-11-25 16:47:29

[1791] polarka

2012-11-25 17:15:38

Ezt hogyan csikartad ki a Mathematicából? Simplify vagy FullSimplify az alábbira nekem nem hozta ki:

Sum[(-1)^k Binomial[n, 2 k + 1] 99^(n - 2 k - 1) 20^(2 k + 1), k, 0, n] - 10*Sum[(-1)^k Binomial[n, 2 k] 99^(n - 2 k) 20^(2 k), k, 0, n]

Előzmény: [1788] Róbert Gida, 2012-11-25 12:57:23

[1790] polarka

2012-11-25 16:47:29

Köszönöm a gyors választ!

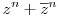$z^n+\overline{z}^n$ -t bontottam fel, hogy lássam mi is történik és ott próbáltam találgatni, hogy hogyan vonhatnám össze valamilyen (a+b)ⁿ alakban. Nem jutott eszembe az Re és Im szerinti felírás.

Szerintem fölösleges a 3. egyenleted szerinti alakba való átalakítás. A második egyenletet folytatva:

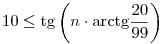
$10 \leq \tan \left( n \cdot {\rm arctg} \frac{20}{99} \right)$

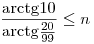
$\frac{{\rm arctg}10}{{\rm arctg} \frac{20}{99} } \leq n$

Előzmény: [1787] Lóczi Lajos, 2012-11-25 12:51:31

[1789] Róbert Gida	2012-11-25 13:01:10
Közben megelőztek, cos előtt lehagytam egy 10-es szorzót. Az azért látható, hogy mennyire hatékony a Mathematica itt is, és csak a "Sum" kellett ide.
Előzmény: [1788] Róbert Gida, 2012-11-25 12:57:23

[1788] Róbert Gida

2012-11-25 12:57:23

Egyrészt ordít róla a binomiális tétel, ki is lehet hozni egy explicit formulát mindkét oldalra. Komplex számokkal könnyebb az út, de ez valósban is megy. A Mathematica viszont egy érdekes alakot is ad a két oldal különbségére:

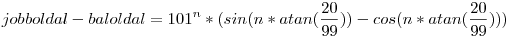
$jobb oldal-bal oldal=101^n*(sin(n*atan(\frac {20}{99}))-cos(n*atan(\frac {20}{99})))$

Előzmény: [1786] polarka, 2012-11-25 01:01:03

[1787] Lóczi Lajos

2012-11-25 12:51:31

Nem mondtad meg, hogy n milyen számhalmaz eleme. Vegyük most természetes számnak az egyszerűség kedvéért.

Legyen például z a 99+20i komplex szám. Ekkor, valós és képzetes részeket használva, az egyenlőtlenség átírható a 10^.re(zⁿ)<im(zⁿ) alakba. Polárkoordinátákkal folytatva, a

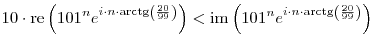
$10\cdot{\rm{ re}}\left(101^n e^{i\cdot n\cdot {\rm{arctg}}\left(\frac{20}{99}\right)}\right)<{\rm{ im}}\left(101^n e^{i\cdot n\cdot {\rm{arctg}}\left(\frac{20}{99}\right)}\right)$

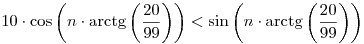
$10\cdot\cos\left(n\cdot {\rm{arctg}}\left(\frac{20}{99}\right)\right)<\sin\left(n\cdot {\rm{arctg}}\left(\frac{20}{99}\right)\right)$

és

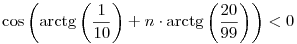
$\cos\left({\rm{arctg}}\left(\frac{1}{10}\right)+n\cdot {\rm{arctg}}\left(\frac{20}{99}\right)\right)<0$

ekvivalens alakokat kapjuk. Mivel a koszinusz (n-ben) szigorúan monoton növő argumentuma n=0 esetén a (0, $\pi$ /2) intervallum eleme, a bal oldal akkor lesz először negatív, amikor az argumentum először belép a ( $\pi$ /2,3 $\pi$ /2) intervallumba. Ez pedig n=8 esetén történik meg leghamarabb.

Előzmény: [1786] polarka, 2012-11-25 01:01:03

[1786] polarka

2012-11-25 01:01:03

Mely legkisebb n-re teljesül az egyenlőtlenség?

Több n-re behelyettesítve kaptam, hogy n>=8.

Viszont arra lennék kíváncsi, hogy próbálgatás nélkül hogyan lehetne a választ megkapni.

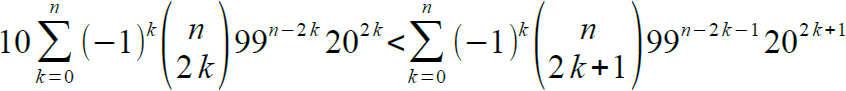[1785] Róbert Gida

2012-11-11 17:55:57

Én speciel már semmin nem csodálkoznék.

http://www.vg.hu/gazdasag/gazdasagpolitika/demjan-akar-assunk-godrot-hazaarulas-nem-lehivni-az-eu-penzeket-390676

"Demján meglátása szerint nem szabadna olyan tudósokat képezni, akik például a bogarak életét kutatják." Tippem szerint jövőre már nem indítanak biológia tagozatos osztályokat. Specmatosok is bármikor sorra kerülhetnek.

Előzmény: [1783] sulc, 2012-11-07 21:03:08

Már regisztráltál?
Új vendég vagy?