Fórum: Valaki mondja meg!

Köszönöm szépen! Nem gondoltam az addíciós képletezésre, de tény, hogy egyszerűen kijön, szinte "triviális" ezek után. :)

Még egyszer köszi!

Hozzunk közös nevezőre, akkor a számláló

$\displaystyle \cos(3x)\cos(4x)\cos(5x)+ \cos(x)\cos(4x)\cos(5x)+\cos(x)\cos(2x)\cos(5x)+\cos(x)\cos(2x)\cos(3x)$

Vonjuk össze az első kettőt és a második kettőt, használjuk a két koszinusz összegére vonakozó addíciós képletet:

$\displaystyle \frac{1}{2}(\cos x \cos(2x)\cos(4x)\cos(5x) +\cos(x)\cos(2x)\cos(4x)\cos(x))$

itt is kiemeljünk $\displaystyle \cos x \cos(2x)\cos(4x)$-t és

$\displaystyle \frac{1}{4}(cos x \cos(2x)\cos(4x)\cos(3x)\cos(2x)$

adódik a számlálónak. Így nincs a feladtanak megoldása, ha jól számoltam.

A $\displaystyle cos(2x)=0$ megoldás nem jöhet szóba, mert az eredeti egyenlet baloldalán nevezőben szereplő tag.

Ennek alapján a Te hozzászólásod és a Wolframalpha azt mondja, hogy nincsen megoldás. Egy program (ami hasonlít a Wa-hoz) szintén nem tudta megoldani.

De mivel ez 1995-ben volt OKTV feladat, I. kategóriában, nem hinném, hogy program kellene hozzá. :)

Azért köszönöm!

Wolframalpha.com alapján:

Átrendezve: 4*cos(2x)*sec(5x)=0 jön ki

itt csak a cos(2x)=0 lehet a megoldás. (a sec(5x) 0 nem lehet, mivel az 1/(sin(x))

(de a megoldásnál meg kell vizsgálni értelmezhető-e, nem megy-e el 'végtelenbe')

cos(2x)=0 megoldása: n*pi/2+pi/4

A sec(5x) miatt lehet,hogy ki kell tiltani valamely gyököket.

Sziasztok!

Tudna valaki segíteni az alábbi feladatban?

$\displaystyle \frac{1}{cos(x)cos(2x)}+\frac{1}{cos(2x)cos(3x)}+\frac{1}{cos(3)cos(4x)}+\frac{1}{cos(4x)cos(5x)} = 0$

Nekem nagyon úgy tűnik, hogy ezt valahogyan teleszkopikus összeggé lehet alakítani, ám nem sikerült. Köszönöm előre is!

Persze, de ebből így nem sokat tanul a gyerek. Javaslom:

- rajzolja fel a két függvényt

- állapítsa meg a megoldások számát

- sejtse meg és igazolja az egész megoldásokat

- találjon valamilyen módszert a negatív megoldás közelítésére.

Valós megoldások:

$\displaystyle x=2;x=4;x=-0.76666469596212309311120442251031484801$

Lehet, hogy már volt. (Ha volt, írjátok meg, melyik témában)

A fiam tette fel a kérdést:

2**x=x**2 egyenletnek mik a megoldásai? (** a hatvány jele)

Szia!

Feltételezem egyenes kúpról van szó, és vélhetőleg a "legkisebb palást" alatt a palást legkisebb területét érted.

Mindezek alapján (hogyha nem így értetted, akkor elnézést, én így értelmezem a feladatot) az alábbiakat teheted:

A kúp alapkörének sugara és magassága legyen $\displaystyle r$ és $\displaystyle h$. Ekkor a kúp térfogata:

$\displaystyle V=\frac{r^2h\pi}{3}$ palástjának területe pedig $\displaystyle r\pi\sqrt{r^2+h^2}$. Ez utóbbinak keressük a minimumát.

Mivel $\displaystyle \frac{\pi}{3}$ konstans, ezért nyugodtan felteheted az általánosság csorbítása nélkül, hogy $\displaystyle r^2h=1$ amiből $\displaystyle r=\frac{1}{\sqrt{h}}$.

Ezt írd be a becsülendőbe, és máris egy "egyszerű" függvénnyel van dolgod, ami csak egy változós. Ha tudsz deriválni, akkor deriválással annak könnyen meghatározhatod a minimumát. Ha nem, akkor valamilyen egyenlőtlenség használatát javaslom. (pld.: nevezetes közepek közötti egyenlőtlenségcsalád)

Az egyenlő térfogatú forgáskúpok közül melyiknek a palástja a legkisebb? A válaszaitokat előre is köszönöm

Számítsd ki külön-külön, hogy az egyes hatványok mennyi maradékot adnak $\displaystyle 11$-gyel osztva! Hasznos lehet, hogy mondjuk $\displaystyle 2^{10}$ és $\displaystyle 3^{10}$ maradéka $\displaystyle 11$-gyel osztva éppen $\displaystyle 1$ (egyébként miért annyi?).

Sziasztok! Van valakinek otlete, hogy lehet bebizonyitani ezt: $\displaystyle 2^{54321}+3^{65432}$ oszthato 11-gyel? Koszi

Legyen a=(1;3;6), b=(3;10;21), c=(-1;-2;-2) és v=(14;42;81). Ekkor v=+2a+3b-3c teljesül, így a "v" vektor koordinátái az "a", "b", "c" bázisban +2, +3, -3, ezeknek az összege csakugyan +2. Valószínűleg ezt kellett bizonyítani. A koordináták meghatározása a következőképpen történik: Legyen v=+xa+yb+zc, ahol "x", "y", "z" a "v" vektor koordinátái az "a", "b", "c" bázisban. Koordinátánként kiírva ez utóbbi egyenletet, a következő három egyenlet adódik: +14=+1x+3y-1z; +42=+3x+10y-2z; +81=+6x+21y-2z; ez három elsőfokú egyenlet három ismeretlennel, így "x", "y", "z" értéke meghatározható.

Köszi a szép és nagyon egyszerű megoldást!!!!!!! Az #1961 hozzászólásban levő összefüggés szerintem is beillene egy versenyfeladatnak. Tisztelettel: Bertalan Zoltán.

Szép megoldás.

Lett egy azonosság, ami első ránézésre nem tűnik triviálisnak:

$\displaystyle \sum_{k=1}^l{k\binom{l}k\sum_{\matrix{i_1+i_2+...+i_k=n\cr i_1,i_2,...i_k\ge1\cr}}^k{\frac{n!}{i_1!i_2!...i_k!}{\bigg(\frac1{l}}\bigg)^n}} = l-l\Big(\frac{l-1}{l}\Big)^n$

ahol az $\displaystyle i_1+i_2+...+i_k=n$ felbontásban a sorrend számít és $\displaystyle n\ge{l}.$

Legyen $\displaystyle n$ ember és $\displaystyle l$ emelet. $\displaystyle X$ legyen a megnyomott gombok száma, $\displaystyle X=\sum_{i=1}^l A_i$, ahol $\displaystyle A_i=0$, ha nem nyomták meg a gombot, és $\displaystyle 1$, ha megnyomják, valamint legyen $\displaystyle B_i$ az az esemény, hogy valaki megnyomja az $\displaystyle i$-ik gombot. De ekkor $\displaystyle E(A_i)=P(B_i)$ és $\displaystyle P(B_i)=P(B_j)$.

$\displaystyle E(X)=E\Big(\sum_{i=1}^l A_i\Big)=\sum_{i=1}^l E(A_i)=\sum_{i=1}^l P(B_i)=lP(B_1)=l-l\Big(\frac{l-1}{l}\Big)^n$

$\displaystyle \sum_{k=1}^{20}{k\binom{20}{k}\sum_{i_1+i_2+...+i_k=30,\forall{i_j}>0}^k{\frac{30!}{i_1!i_2!...i_k!}{\bigg(\frac1{20}}\bigg)^{30}}}$

Az $\displaystyle i_1+i_2+...+i_k=30$ felbontásban a sorrend számít.

Rossz megoldás.

0 pont

Szerintem meg szumma ká megy egytől húszig kászor húszalatt a ká szor huszonkilenc alatt a kámínuszegy szor egyhuszad a harmincadikán.

Szerintem: $\displaystyle \frac {843275206102804784954490480594066706599}{53687091200000000000000000000000000000}$

15.7

Tegyük fel, hogy a szuper-hilton szálloda földszintjén beszáll a liftbe 30 ember. A szálloda 20 emeletes, tehát a liftben a "földszint" gombon kívül 1-től 20-ig számozott gombok találhatóak. A 30 ember mindegyike megnyomja a számozott gombok valamelyikét (egy ember pontosan egy gombot nyom meg), annak megfelelően hogy ki melyik szintre akkar a lifttel megérkezni. Természetesen tekinthetjük úgy, hogy akármelyik ember akármelyik gombot egyforma (1/20) valószínűséggel nyomja meg. Mennyi lesz a megnyomott gombok számának várható értéke? Tisztelettel: Bertalan Zoltán.

A B.4612 sz. feladat (2014 március) megoldását keresem (a "Lejárt..." menüpont alá is feltettem a kérést). Előre is kösz!

Igen, ilyenre gondoltam, köszönöm szépen!

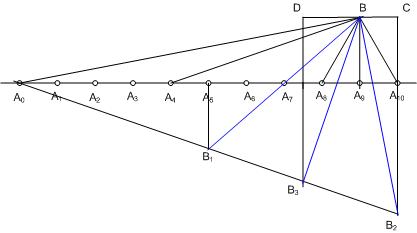
Talán ilyesmire gondoltál: Kövessük a közölt megoldás gondolatmenetét és mutassuk meg, hogy 2-2 szög 30 fokra egészíti ki egymást. Tükrözzük az $\displaystyle A_4 A_9 B \Delta$ -et az $\displaystyle A_0 A_{10}$ egyenesre és toljuk el $\displaystyle A_4 et A_0 ba$ . B új helyzete legyen $\displaystyle B_1$ . Ekkor $\displaystyle B A_0 B_1 \angle$ -ről kell megmutatni, hogy $\displaystyle 30^\circ$ -os.

Vegyük fel az $\displaystyle A_0 B_1$ egyenesen $\displaystyle B_2$ -t úgy, hogy $\displaystyle A_0 B_1 = B_1 B_2$ legyen . Ekkor $\displaystyle B_1 A_5 = \sqrt 3 , B_2 A_{10} = 2 \sqrt 3$ . A $\displaystyle B_2 A_{10}$ egyenesen legyen C az a pont, melyre $\displaystyle B B_2 C \Delta$ derékszögű. $\displaystyle B C / C B_2 = 1 / (3 \sqrt 3) = \sqrt 3 / 9$ . $\displaystyle A_0 A_9 B \Delta$ -ben $\displaystyle B A_9 / A_0 A_9 = \sqrt 3 / 9$ . A két háromszög hasonló, $\displaystyle A_0 B B_2 \angle = 90^\circ$ , ezért $\displaystyle B_1 A_0 = B_1 B_2 = B_1 B$. Legyen $\displaystyle B_1 B_2$ felezőpntja $\displaystyle B_3$ . A $\displaystyle B_3$ -ból $\displaystyle A_0 A_{10}$ egyenesre bocsátott merőlegesen D az a pont, melyre $\displaystyle B_3 B D \Delta$ derékszögű. $\displaystyle BD / D B_3 = (3/2)/(5/2)\sqrt 3 = \sqrt 3 / 5$ . $\displaystyle B_1 A_5 / A_5 A_0 = \sqrt 3 / 5$ . $\displaystyle B B_3$ merőleges $\displaystyle A_0 B_1$ -re, $\displaystyle B B_1 = B B_2$ , a $\displaystyle B B_1 B_2 \Delta$ szabályos, $\displaystyle A_0 B_2 B \angle = 60^\circ$ , $\displaystyle B A_0 B_1 \angle = 30^\circ$ .

Folytatás: készítsünk hasonló ábrát a másik szögpárra.