|
| [2051] emm | 2015-12-06 16:43:16 |
 D:=(A∪B∪C)c, ekkor P(D)=1−p−q−r. Ekkor lényegében egy 4 oldalú cinkelt "kockával" dobunk. Legyen a keresett valószínűség Rn. Feltételezzünk arra, hogy az első dobás, amikor D-től különbözőt dobunk, k, legyen ez az esemény Sk, és a k-ik dobás Xk, a függetlenséget használva adódik, hogy:
P(Sk)=P(Xk≠D∩k−1⋂j=1Xj=D)=P(Xk≠D)k−1∏j=1P(Xj=D)=(1−p−q−r)k−1(p+q+r)
Ebből a nekünk megfelelő eset az, amikor A-t dobunk, így az A, B, C események páronként kizáró volta miatt: miatt:
P(Sk∩Xk=A)=P(Xk=A∩k−1⋂j=1Xj=D)=P(Xk=A)k−1∏j=1P(Xj=D)(1−p−q−r)k−1p
Vagyis n dobás esetén, alkalmazva a mértani sor összegképletét:
P(Rn)=n∑i=1P(Si∩Xi=A)=pn−1∑i=0(1−p−q−r)i=p1−(1−p−q−r)np+q+r
Ha p,q,r>0, akkor n→∞ esetén a keresett valószínűség tart pp+q+r-hez. (és nem okoz problémát, ha p+q+r=1).
|
| Előzmény: [2049] lorantfy, 2015-12-05 19:56:56 |
|
|
| [2049] lorantfy | 2015-12-05 19:56:56 |
 Az A, B és C egymást kizáró események P(A)=p, P(B)=q, P(C)=r. Mennyi a valószínűsége n független kísérletet elvégezve, hogy A előbb következik be mint B vagy C? Mi lesz e valószínűség határértéke, ha n tart a végtelenbe?
|
|
| [2048] lorantfy | 2015-12-05 19:46:07 |
 Adott egy gömbön az AB ív. Hol vannak a gömbfelületen azok a C pontok, melyekre az ABC gömbháromszög területe egy adott állandó.
|
|
| [2047] Jhony | 2015-12-05 19:23:55 |
 - köszönöm szépen a válaszokat ! - a továbbiakban folytatnám a gondolatot,tekintsük nulladik lépésnek az előzőekben felírt és elfogadott,bizonyítást nem igénylő képletet,azaz
0. 2a∗(2b+1)=N képletet, ,,a" és ,,b" eleme az N+(0) -nak 1. tudjuk,ha 2a azaz 2-őt az ,,a" hatványon ,,a"-szor osztjuk 2-vel az eredmény 1 2. ha (2b+1) -et beszorozzuk 3-mal és hozzáadunk 1-et ,azaz (2b+1)*3 +1 = 6b+4 azaz 6b+4 = 2(3b+2) vagyis az eredmény ismét egy páros szám amit osztva 2 -vel kapjuk a (3b+2),ami páratlan 3. ha a (3b+2) -őt beszorozzuk 3-mal és hozzáadunk 1-et ,azaz (3b+2)*3 +1 = 9b+7 4. bizonyítsuk be,hogy (9b+7)=2x ahol ,,x" természetes szám,vagyis bizonyítsuk be,hogy a fent említett képletből bármely (2b+1) számra folytatván a sort,azaz szorozva 3-mal plusz 1 ,osztva 2 -vel majd ismét szorozva 3-mal plusz 1 előbb-utóbb 2 hatványát eredményezi .
|
|
|
| [2045] csábos | 2015-12-05 09:12:48 |
 Kedves Jhony!
Amit írsz, az a számelmélet alaptételéből következik:
Minden nem 0 és nem 1 nem -1 egész szám felírható prímszámok (prímhatványok) szorzatatként és ez az előállítás előjeltől és sorrendtől eltekintve egyértelmű.
pl 1800=2⋅3⋅3⋅5⋅2⋅2⋅5, vagy 1800=−3⋅2⋅(−2)⋅5⋅2⋅3⋅5
Kanonikus alaknak hívjuk azt, amikor a prímtényezőket csoportosítjuk, és a megfelelő kitevőn írva szorozzuk őket össze, pl 1800=23⋅32⋅52
Esetünkben: ha n páratlan, akkor n=2b+1 valamilyen b egész számra és
n=20(2b+1)
Ha n osztható kettővel, akkor n prímtényezős felírásában szerepel a kettő. Írjuk föl n kanonikus alakját: n=2α⋅pβ11⋯pβtt Most a kettőhatvány utáni rész páratlan, azaz 2b+1 alakú, így n=2α(2b+1).
Hátra van még az 1, mert arról nem szól a számelmélet alaptétele: 1=20(2⋅0+1)
|
| Előzmény: [2044] Jhony, 2015-12-05 01:43:56 |
|
| [2044] Jhony | 2015-12-05 01:43:56 |
 Tisztelt fórumozók ! - kérdésem ki hogyan bizonyítaná be,hogy az alábbi képlet alkalmas minden N természetes szám felírására :
(2)'a *(2b +1) = N vagyis 2 az ,,a" hatványon szorozva (2b+1) = N bocsánat,de kitéve a hatványkitevőt a következő üzenetet kaptam :,,Hiba: A ,,hatványkitevő" parancs csak matematikai módban használható " - tudván,hogy a és b eleme az N + (0) vagyis a és b eleme a természetes számok halmazának plusz nulla
- elképzelésem a ,,reductio ad absurdum" vagyis visszavezetés a lehetetlenre
(2)'0 *(2*0 +1) =/= 1 vagyis azaz 2 a nulla hatványon szorozva ... 1 *(0 +1) =/= 1 vagyis
1 =/= 1 ami tudjuk,hogy nem igaz,
- vélemények ?
- segítségeteket nagyon szépen köszönöm !
|
|
| [2043] lorantfy | 2015-11-27 13:50:35 |
 Megoldást szeretnél vagy csak segítséget? Feltehetjük, hogy minden matematikus egyformán, okosan gondolkodik. Ahogy biztosan megtudja, hogy maszatos lett leszáll és megmossa az arcát. Kezd el 2 emberrel és gondold végig a lehetőségeket, aztán ha kell növeld a számukat!
|
| Előzmény: [2042] marcius8, 2015-11-23 08:16:55 |
|
| [2042] marcius8 | 2015-11-23 08:16:55 |
 Matematikusok egy vonaton születésnapi bulit rendeznek, és egy csokistortát majszolgatva összemaszatolják magukat. A kalauz jegyellenőrzés közben megjegyzi, hogy némelyik matematikusnak csokikrémes lett a füle. A matematikusok persze rögtön elszégyellik magukat, és ezután egy szót sem szólnak egymáshoz. Persze látják egymást, de magukat nem, ugyanis a vonaton nincsen tükör. A matematikusok a vonaton még megmosakodni sem tudnak, mert a vonaton nincs víz. A kalauz persze jó tanácsként közli a matematikusokkal, hogy minden megállóhelyen van mosakodásra lehetőség. Ezután a következő megállónál nem száll le egyetlen egy matematikus sem a vonatról, hogy megmosakodjon. A rákövetkező megállón sem száll le egyetlen egy matematikus sem a vonatról, hogy megmosakodjon. Viszont a harmadik megállónál néhány matematikus leszáll a vonatról, hogy megmosakodjon.
Kérdés: Hány matematikus szállt le a vonatról mosakodás céljából?
|
|
| [2041] Lóczi Lajos | 2015-10-13 01:22:36 |
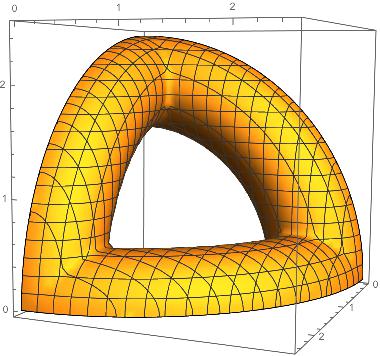
 A test térfogatának kérdését tekintve − az alábbiak a felszínre "még inkább" vonatkoznak − számomra úgy tűnik, hogy a térfogat nem fejezhető ki elemi függvényekkel. Még konkrét speciális esetben sem sikerült.
Tekintsük pl. az R=2, r=1/2 esetet. Ekkor a test nyolcadrésze látható az ábrán. Különféle darabolásokkal a térfogat felírható kettős-, illetve egyszeres integrálokkal, ám úgy tűnik, hogy ezeknek nincs elemi primitív függvénye.
Természetesen numerikusan az integrálok, s így a térfogat is számolható.
Meg tudnánk például határozni az R=2, r=1/2 esetben a teljes test közelítő térfogatát?
|
 |
| Előzmény: [2040] marcius8, 2015-10-07 08:22:45 |
|
| [2040] marcius8 | 2015-10-07 08:22:45 |
 Meg tudja nekem valaki mondani annak a testnek a térfogatát és felszínét, amely három, egymással egybevágó, egymásra merőleges, ugyanazzal a középponttal rendelkező tóruszból áll. Ismert a tóruszok középkörének "R" sugara és ismert a tóruszok kör alakú síkmetszetének "r" sugara, ahol r<R.
|
|
|
| [2038] Kemény Legény | 2015-09-23 12:17:44 |
 "- Van-e olyan négytagú (esetleg többtagú) számtani sorozat, amelynek minden tagja négyzetszám?"
Erre úgy tűnik, szintén tagadó a válasz: pl. Győri, Hajdu és Pintér cikke (Perfect powers from products of consecutive terms in arithmetic progression, Compositio Mathematica, 2009) alapján egy még erősebb állítás is igaz:
"We prove that for any positive integers x,d and k with gcd (x,d)=1 and 3<k<35, the product x(x+d)...(x+(k-1)d) cannot be a perfect power".
A cikk alapján úgy tűnik, az x(x+d)...(x+(k−1)d)=byn,(x,d)=1 egyenlet megoldását már Euler is vizsgálta a b=1,k=4,n=2 esetre. Sőt Erdős sejtése az, hogy k>3 esetén sosem lehet egy (rel. prímekből álló) számtani sorozat k egymást követő elemének szorzata teljes hatvány.
|
| Előzmény: [2035] marcius8, 2015-09-23 11:39:32 |
|
|
| [2036] Kemény Legény | 2015-09-23 11:55:46 |
 "- Van-e olyan háromtagú (esetleg többtagú) számtani sorozat, amelynek minden tagja köbszám (esetleg negyedik hatvány, esetleg ötödik hatvány, ..... stb.)"
Egy gyors keresés után ezt az arxiv-os Ribet-cikket találtam.
A Conjecture 1 alapján pedig úgy tűnik, az az általános sejtés (Dénes, 1952), hogy számtani sorozatot csak triviális módon alkothatnak páratlan prímkitevő esetén.
Ebben a Theorem 3 azt állítja, hogy ap+2αbp+cp=0-nak nincs megoldása az egész számok körében, ha 2≤α≤p. Továbbá ap+2bp+cp=0-nek nincs olyan relatív prím egész megoldása, ahol abc páros lenne. Illetve a Theorem 4 p=4k+1 alakú kitevőre igazolja a sejtést.
|
| Előzmény: [2035] marcius8, 2015-09-23 11:39:32 |
|
| [2035] marcius8 | 2015-09-23 11:39:32 |
 Sok olyan háromtagú számtani sorozat van, amelynek tagjai négyzetszámok. (Ilyen például 1, 25, 49 vagy 49, 169, 289 vagy 49, 289, 529 vagy 961, 1681, 2401 stb....) Az ilyen háromtagú sorozatok tagjainak előállítása visszavezethető pitagoraszi számhármasokra, és az ilyen sorozatok tagjaiból pitagoraszi számhármasok állíthatóak elő.
De:
- Van-e olyan négytagú (esetleg többtagú) számtani sorozat, amelynek minden tagja négyzetszám?
- Van-e olyan háromtagú (esetleg többtagú) számtani sorozat, amelynek minden tagja köbszám (esetleg negyedik hatvány, esetleg ötödik hatvány, ..... stb.)
Tisztelettel: Bertalan Zoltán.
|
|
| [2034] marcius8 | 2015-09-07 11:19:09 |
 Legyen "D(n)" az "n" elemű permutációk közül azoknak a száma, amelyeknek nincs fixpontja. Bizonyítsuk be kombinatorikus módon a következő összefüggést:
D(k)=(k-1)*(D(k-1)+D(k-2))
|
|
| [2033] marcius8 | 2015-07-09 00:32:10 |
 Tud valaki egy 8x8-as latin-görög négyzetet? És tud valaki egy 8x8x8-as görög-latin-cirill kockát? Ha igen, kérem, hogy írja le. Előre is köszönöm. BERTALAN ZOLTÁN.
|
|
|
| [2031] Bátki Zsolt | 2015-05-11 05:49:38 |
 Ez volt idén (2015) középszintű matematika feladat, 2 pontért.
3. „Minden szekrény barna.” Válassza ki az alábbiak közül annak a mondatnak a betűjelét, amelyik tagadása a fenti kijelentésnek! A) Van olyan szekrény, amelyik nem barna. B) Nincs barna szekrény. C) Van olyan szekrény, amelyik barna. D) Pontosan egy szekrény barna.
Megkérdeztem a munkahelyemen 10 embert.(mérnököket) 6 a 'B'-re tippelt. Kettő azt mondta az 'A' és a 'B' is jó. Ketten a jó 'A' megoldást.
Kérdésem, vajon az érettségin, hány százalék adott erre jó választ? Valahol ez a statisztika fellelhető a Neten?
|
|
|
| [2029] jonas | 2015-04-09 08:48:28 |
 Egy négyzetes mátrixot Hankel mátrixnak hívunk, ha bármely antidiagonálisában csak azonos elemek vannak. Például
T=(0621962198219811981298121)
egy Hankel-mátrix.
Minket most olyan Hankel-mátrixok érdekelnek, amiknek minden eleme 0 vagy 1. Igaz-e, hogy ha egy négyzetes nulla-egy mátrix a sorainak és oszlopainak valamely permutációjával Hankel-mátrixszá alakítható, akkor csak a sorainak a permutációjával is Hankel-mátrixszá alakítható?
A kérdés onnan jön, hogy felix azt kérdezi a MathOverflow-n, hogy hány ilyen permutált mátrix van.
|
|
| [2028] marcius8 | 2015-04-05 10:45:25 |
 Kiegészítés az előző kérdésemhez: Feltehető, hogy annak a valószínősége, hogy annak a valószínűsége, hogy a 4-es metró hibamentesen "t" működik, "lambda" paraméterű exponenciális eloszlást követ. Tisztelettel: Bertalan Zoltán.
|
|









