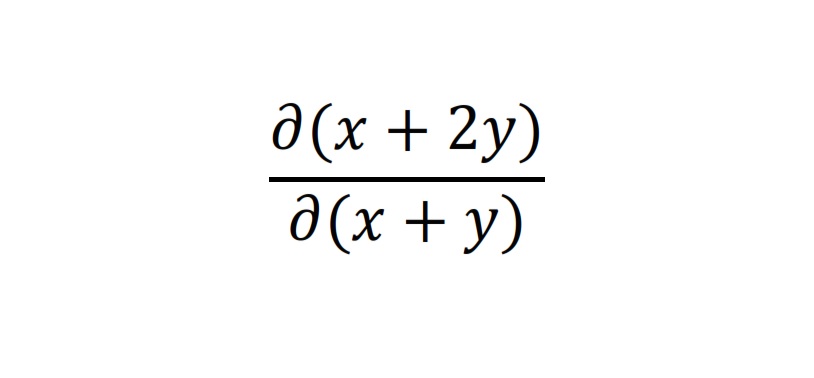| [2086] jonas | 2016-08-18 19:48:34 |
 Ennek a táblázatnak nem kéne szimmetrikusnak lennie? A MAGY E, MAGY K az egyik irányban meg van jelölve, de a másik irányban nincs. Meg tudnád adni a helyes gráfot, és lehetőleg nem csak képként?
|
| Előzmény: [2084] lorantfy, 2016-08-18 15:32:21 |
|
|
| [2084] lorantfy | 2016-08-18 15:32:21 |
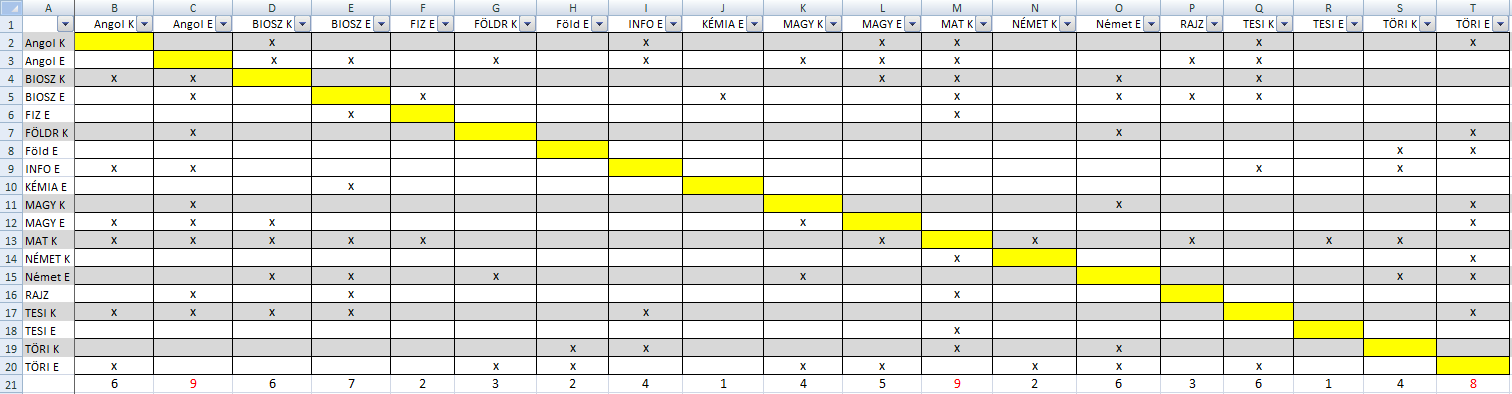
 Segítségeteket kérem egy valós problémához, ami azt is mutatja, hogy az órarend összeállítása a mai középiskolákban a lehetetlennel határos. A faktos csoportok láthatók a táblázatban. Az X-ek azt jelentik, hogy van olyan tanuló, aki az oszlop és sor faktot (tantárgyat) együtt választotta. Cél: Minél kevesebb olyan csoportot kell kialakítani a tantárgyakból, amelyek mehetnek egy időben, tehát nincs olyan tanuló, aki egyszerre választotta őket és egyszerre két helyen kéne lennie. Minden ötletet szívesen veszek. Előre is köszönöm!
|
 |
|
| [2083] Jhony | 2016-07-31 04:15:10 |
 Üdvözletem - szóval még is csak lenne valaki ,akit érdekelne a téma - nagyon örülök ennek és folytatom az elképzelésem vagyis amit ott az openstudy.com/mathematics oldalon leírtam . - elképzelésem szerint az első alapprím a kettes,az egyedüli páros,majd egy szám különbségre követi a hármas,az első páratlan prím -(itt jegyezném meg,hogy ők,mint egy szám különbségű prímek,lehetnének ,,társ-prímek" - 2 - 3
- az első kör 2 szorozva 3 = 6 +/- 1 = 5 - 7 és így bővül első körben négyre a prímnemzetség
- 5 - 7
- 5 + 7 = 12 +/- 1 = 11 - 13 ikerprímek
- 11 - 13
- 11 + 13 = 24×3=72 +/- 1 = 71 -73 ikerprímek
- 71 - 73
- 71+73=144×3=432 +/- 1 = 431 - 433 ikerprímek
- 431 -433
- 431+433=864×3=2592 +/- 1 = 2591 - 2593 ikerprímek
- és ez lenne az eddigi leghosszabb ikerprím-családfa amit logikusan a kapcsolatok leírásával érthetően értelmezni lehet
köszönöm szépen a véleményeket
|
| Előzmény: [2076] HoA, 2016-05-19 10:09:05 |
|
| [2082] Fálesz Mihály | 2016-05-27 11:59:49 |
 Varázsló barátja, Hű De Morgána azt ajánlotta a törpének, hogy a dobozokat úgy helyezze el, hogy csak egyetlen &tex;\displaystyle L&xet; limeszpontjuk legyen. Újult lelkesedéssel látott munkához; egyhelyben ülve, két kézzel rakosgatta a köveket. Nagyon élvezte, hogy amikor egy követ belerak egy dobozba, a másik kezével már veheti is ki a dobozból a másik követ. A végén újra belenézett a dobozokba, és azok --- ahogy várta --- ismét üresek voltak, viszont az összes követ ott látta az &tex;\displaystyle L&xet; pontban.
--- Én soha nem tettem egy követ sem az &tex;\displaystyle L&xet; pontba! Hogy kerültek mégis oda? --- faggatta Merlint.
--- Oda konvergáltak. Ha a köveket pontszerűnek tekintjük, azt mondhatjuk, hogy minden egyes kő egy-egy folytonos görbén mozgott, és ezeknek a görbéknek a közös limesze a 11 órás időpontban éppen az &tex;\displaystyle L&xet; pont.
A törpe ezt sem igazán értette, de nagyon örült, hogy nem vesztek el a kövei. Boldogan kiáltott:
--- MEGVANNAK A SZÍNES KÖVEIM! MEGNYERTEM A BÖLCSESSÉG KÖVÉT!
--- Na jó, téd lehet a Bölcsesség Köve -- válaszolta Merlin. --- Adj ide nekem egyet a köveid közül.
A törpe széles, diadalmas mosollyal ki akarta nyújtani a kezét, hogy kivegyen egy követ az &tex;\displaystyle L&xet; pontból, de ekkor kellemetlen meglepetés érte.
--- Öööö... hova lettek a kezeim?
--- A kezed részecskéi a klasszikus modell szerint pontszerűek, és folytonos görbéken mozognak, de ez csak egyszerűsített modell. A finomabb kvantummechanikai rendszerben a részecskék helyének valószínűségi eloszlását az állapotfüggvényük írja le. A szokásos esetekben az állapotfüggvény egy kis halmazra koncentrálódik, ezért kezelhetjük a részecskéket pontszerűnek. A te eseted viszont valamivel komplikáltabb. Tetszőleges &tex;\displaystyle \varepsilon>0&xet;-ra igaz, hogy &tex;\displaystyle 11-\varepsilon&xet; és &tex;\displaystyle 11&xet; között te az összes dobozba beledugtad mindkét kezedet. Ezért az állapotfüggvények idő szerinti limesze sokkal nagyobb térrészen, a dobozok körül szóródik szét.
--- Már megint nem értem. Muszáj mindig ilyen tudományos bikkfanyelven fogalmazni?
--- Rendben. A kezeid szétkenődtek a térben egy, a dobozok körüli felhőben.
--- Hú. Akkor vegyél el te magadnak egy színes követ az &tex;\displaystyle L&xet; pontból, és léccí, add ide nekem a Bölcsesség Kövét!
--- A kristály törékeny. Tartok tőle, hogy nem tudnád megfogni, átesne a felhőn...
|
| Előzmény: [2081] Sinobi, 2016-05-26 22:44:00 |
|
| [2081] Sinobi | 2016-05-26 22:44:00 |
 "Amit én hiányolok a meséből, az az, hogy hol volt a törpe a feladat végén. :-)"
A törpe felkereste Merlin ősellenségét, Morgánát, aki azt javasolta a törpének, hogy dél előtt egy fél órával markoljon bele az első dobozba, szedje ki belőle a semmit, rakja vissza a nagy dobozba, és ezt folytassa egészen délig. Csodálkozott a törpe, de végrehajtotta. Végén az összes (egy szám sem hiányzott) köve ott lapult a nagy dobozban, amit még kevésbé értett. Morgána hisztérikus gonosz nevetéséből a "kompakkság" szót vélte kihallani, de arra nem dobott semmit a keresője, belenyugodott.
Merlin nem csak a bölcsek kövét vesztette így el, de kiderült hogy a hulladékmegsemmisítő üzemei sem pont azt csinálják amit szeretne -- ki kellett hát valamit találnia...
Segítsünk Merlinnek! Adjunk olyan algoritmust, amelyik képes a gömbön vagy a projektív síkon* is megsemmisíteni a dolgokat!
* a törpék 0 magasak
|
| Előzmény: [2080] Fálesz Mihály, 2016-05-26 06:49:20 |
|
| [2080] Fálesz Mihály | 2016-05-26 06:49:20 |
|
Én úgy értem a kérdést, hogy a második feladatban is a későbbi kő mozog tovább a kisebb sorszámmal, tehát megismételjük az első feladatot; a kövek nem sétálnak ki a végtelenbe, csak a sorszámok. Az &tex;\displaystyle n&xet;-edik lépésben az &tex;\displaystyle n&xet;-edik kő (&tex;\displaystyle 1&xet;-es sorszámmal) bekerül az &tex;\displaystyle n&xet;-edik dobozba, és többször már nem vesszük ki a dobozból, viszont a számát minden menetben letöröljük és &tex;\displaystyle 1&xet;-gyel nagyobbra cseréljük.
A feladat végén minden dobozban egyetlen, számozatlan kő lesz, az &tex;\displaystyle n&xet;-edik dobozban az eredetileg &tex;\displaystyle n&xet;-edik kő.
Amit én hiányolok a meséből, az az, hogy hol volt a törpe a feladat végén. :-)
|
| Előzmény: [2079] csábos, 2016-05-25 22:58:51 |
|
|
| [2078] Sinobi | 2016-05-22 18:11:10 |
|
Ki tudja-e úgy cselezni az irigy törpe Merlint, hogy a második feladat végrehajtása során mindig amikor két kő kerülne egy dobozba, akkor (Merlinnek háttal állva, és parányi testével takarva amit csinál) nagyon gyorsan kicserélné a kövek sorszámait?
|
|
| [2077] Lpont | 2016-05-19 11:53:44 |
 "- ezzel kapcsolatban van egy vagyis szerkesztettem egy saját képlet által felállított prím-családfát,amit ott az oldalon megosztottam ideértve a szerkesztéshez,felállításhoz használt teljes útmutatót,leírást -"
Oszd meg velünk is kérlek.
|
| Előzmény: [2071] Jhony, 2016-03-27 13:36:35 |
|
| [2076] HoA | 2016-05-19 10:09:05 |
 Családfáról szólva arra gondol az ember, hogy a benne szereplő elemek - alapértelmezésben emberek - közötti rokonsági kapcsolatokat ábrázoljuk. Hogy értelmezed prímek esetére a fogalmakat? Mikor van két prím szülő-gyerek kapcsolatban, kik testvérek, kik házastársak?
|
| Előzmény: [2071] Jhony, 2016-03-27 13:36:35 |
|
|
| [2074] HoA | 2016-05-18 13:01:08 |
|
Pontosítani kéne, mit jelent a szélességgel rendelkező mutató. Ha úgy érted, hogy mindegyik legalább d szélességű, a tengelynél is, akár lekerekítve,akkor az r = d/2 sugarú kis kör minden pontját mindig mindegyik mutató fedi. Vagy keskeny körcikk alakú mutatókra gondolsz, a tengelynél 0 szélességgel?
|
| Előzmény: [2072] Sinobi, 2016-04-10 22:30:58 |
|
| [2073] marcius8 | 2016-05-17 14:28:54 |
 Meg tudja valaki mondani, hogy egy normális (9x9-es) szudoku táblázatot hányféleképpen lehet kitölteni? Tisztelettel: Bertalan Zoltán.
|
|
| [2072] Sinobi | 2016-04-10 22:30:58 |
|
n darab, szélességgel rendelkezö óramutató forog egy számlapon, vi e R sebességgel. Igaz-e, hogy ha volt legalább 1, akkor lesz végtelen sok idöintervallum, amikor az összes mutató 'összeér', fednek egy pontot?
|
|
| [2071] Jhony | 2016-03-27 13:36:35 |
|
üdv. mindenkinek ! - a kérdésem ,,Prímek családfáját szerkeszteni,felállítani" - eszébe jutott e már valakinek is a Világon ? - vagyis ti erről mit tudtok,ugyanis mindezt mikor felvetettem az ,,openstudy.com/mathematics" angol nyelvű fórumon,azt kérdezték,mindez honnan jutott eszembe,hisz ezzel még nem állt elő - tudomásuk szerint - eddig senki sem az egész világon,vagyis első ember lennék,vagyok aki ezt a témát felveti,említi a matematika egész máig tartó történelme során - legalább is nem ismeretes ezzel kapcsolatban semmi - nos szerintetek,mi erről a véleményetek, tudomásotok, ismeretetek ? - ezzel kapcsolatban van egy vagyis szerkesztettem egy saját képlet által felállított prím-családfát,amit ott az oldalon megosztottam ideértve a szerkesztéshez,felállításhoz használt teljes útmutatót,leírást - ... - megosztva,feltéve kérdésemet,hogy mit vagyis hogyan ismertessem,közöljem a további prímekkel kapcsolatos úgy mond - szerintem - újdonságokat,sejtéseket,hipotéziseket ? - a válaszokat,hozzászólásokat előre is köszönöm szépen !
|
|
| [2070] 314 | 2016-02-28 17:01:54 |
|
Üdv mindenkinek!
Azt szeretném kérdezni, hogy egy többváltozós függvényt hogyan kell deriválni egy szintén többváltozós függvény szerint? Pl. az ábrán látható kifejezést hogy lehet megoldani? Előre is köszönöm a választ!
|
 |
|
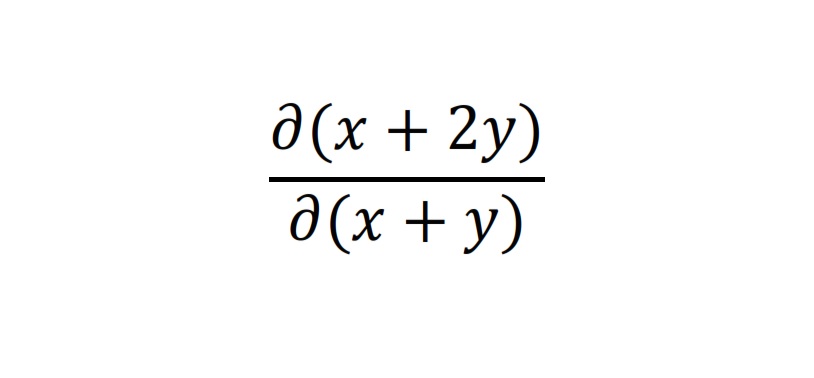| [2069] epsilon | 2016-02-25 17:06:40 |
|
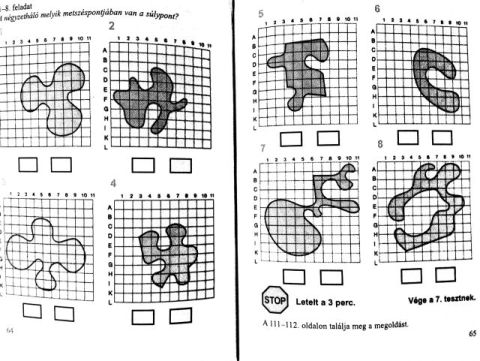
Kedves lorantfy! Köszönöm a tippet! Valóban, a diákkori fizika órákon így állapítottuk meg a homogén lemezek (fém v műanyag, fa, stb)súlypontját, hogy két felfüggesztésnek vettük a metszéspontját, és meg is van a súlypont. (ha a súlypont a lemezen kívül esik, akkor már nehezebb dolgunk van). Ellenben az esetünkben több nehézségbe ütközünk: a felfüggesztést képzeletben kell elvégezni, és így a gravitáció irányát nem tudjuk PONTOSAN meghatározni, csak megközelítőleg elképzelni, és minden bizonnyal ha a leírt módszerrel a súlypontot meg is kapnánk, nem állíthatnánk teljes biztonsággal, hogy az az, mert ez csak egy fizikai mérés ami csak empirikusan megközelítő. De még tovább menve: a súlypont valamelyik rácspontra kell essen, és ha méréssel csak a közelébe esik, akkor nem tippelhetjük, hogy na ez a rácspont a leg közelebbi és kinevezzük súlypontnak. Összegezve: noha a felfüggesztési ötlet nem kizárt, de a matematikai pontosság szempontjából nem tartom valószínűnek, hogy a könyv szerzője erre a megoldásra gondolhatott, hiszen nem is aknáztuk ki lényegesen a rácspontokat amire a súlypont is esik. Várom tehát a további tippeket, hátha eltalálnánk, hogy mire gondolhatott a szerző a feladatok megoldásánál, amikor a súlypontot valamelyik rácspontra tervezte.
|
| Előzmény: [2068] lorantfy, 2016-02-23 21:23:23 |
|
| [2068] lorantfy | 2016-02-23 21:23:23 |
|
Gondolatban fellógatod több kiválasztott szélső pontjánál fogva. Forgathatod a könyvet is. Behúzod a függőlegest, mikor úgy gondolod egyensúlyban lenne. 4-5 egyenest behúzva kiválasztod azt a hármat, ami egy kockában metszi egymást és kész. Az is az intelligenciához tartozik, hogy le tudsz játszani bizonyos dolgokat gondolatban!
|
| Előzmény: [2067] epsilon, 2016-02-23 13:22:03 |
|
| [2067] epsilon | 2016-02-23 13:22:03 |
|
Üdv Mindenkinek! Van egy régebbi IQ könyvem, J. E. Klausnitzer: IQ-Önteszt, Ciceró kiakó, 2005. Ebben van egy pár kérdés amelyekben rácspontokra rajzolt zárt görbevonal által határolt lapok súlypontjának a koordinátáit kell megmondani. Mindjárt jön a rajz is. Így saccolással általában eltalálható a súlypont koordinátája, de az lenne a kérdésem, hogy milyen szabály alapján kell meghatározni, hiszen nem is matematika könyvről van szó, hogy különféle elméleteket alkalmazzunk, hanem egyszerű IQ könyvről. Tudna-e valaki segíteni, hogy miként kell meghatározni a látható lapok súlypontjainak a koordinátáit? Ha szükség van az eredményre azt is küldöm, hiszen megvan, engem a "miért az a súlypont" kérdésre érdekelne a válasz! Előre is köszönöm!
|
 |
|
| [2066] Fálesz Mihály | 2015-12-30 09:42:03 |
|
Arra gondoltam, hogy a Fejes-Tóth féle programot csináljuk végig.
Vegyük a poláris háromszöget. Az eredeti háromszög területéből következtethetünk a poláris háromszög kerületére. A poláris háromszögnek ismerjük egy csúcsát, az ebből kiinduló oldal-főköröket és a kerületet. Ezek meghatározzák a harmadik oldalhoz hozzáírt kört...
|
| Előzmény: [2064] Sinobi, 2015-12-28 23:20:22 |
|
| [2065] mooosa | 2015-12-29 17:15:00 |
|
Legyen f eleme C(I) folytonos függvény az I = (0, 1) nyílt intervallumon, és tegyük fel, hogy lim x->0+ f(x) = +végtlen , határozzuk meg a g(x) := sin f(x) kompozíciófüggvény torlódási pontjainak halmazát x->+0-ra!
|
|
|
|
| [2062] Kemény Legény | 2015-12-15 13:50:00 |
|
A dominált konvergencia tétellel/Fatou-lemmával valóban be lehet látni ilyeneket. Legyen az &tex;\displaystyle f_n&xet; függvény az &tex;\displaystyle n&xet;-edik halmaz (ami tetszőleges mérhető halmaz, így intervallum vagy akár intervallumok uniója is lehet) karakterisztikus függvénye (a halmazon 1, kívül 0). Ekkor a konstans 1 függvény egy integrálható majoránsa az &tex;\displaystyle f_n&xet;-eknek, így pl. a Fatou-lemma alapján &tex;\displaystyle limsup_{n\to\infty} \int f_n d\lambda\le \int limsup_{n\to\infty} f_n d\lambda&xet;, ahol az utóbbi limeszt pontonként értjük. Ha az &tex;\displaystyle f_n&xet;-eket meghatározó halmazok mértékére van egy közös alsó korlát K, akkor a bal oldali határérték is legalább K. Ha viszont egy pontot csak véges sok &tex;\displaystyle f_n&xet; fed le, akkor a jobb oldali integrálban szereplő &tex;\displaystyle limsup_{n\to\infty} f_n =0&xet; abban a pontban, egyébként 1. Mivel a jobb oldal nem lehet 0, így az az erősebb állítás is kijött, hogy a végtelen sokszor lefedett pontok halmaza nem lehet nullmértékű (sőt legalább K mértékű kell legyen).
|
| Előzmény: [2058] Sinobi, 2015-12-14 22:11:22 |
|
