Fórum: Valaki mondja meg!

Tegyük fel, hogy minden futballmérkőzés pontosan 90 percig tart, és minden mérkőzésen átlagosan 3 gól esik. A mérkőzésenkénti gólok száma Poisson-eloszlást követ. Most nagy hirtelen a nagyokos szabályalkotók összegyűlnek, és kitalálják azt az új szabályt, hogy ha akármelyik mérkőzésen egy gól esik, akkor a mérkőzés nem ér véget automatikusan 90 perc után, hanem a gól után pontosan 10 percig még tart a mérkőzés, azaz 10 perc hosszabbítás következik. Nyilván, ha az utolsó gól a mérkőzés 80.-ik perce előtt esik, akkor a mérkőzés automatikusan véget ér 90 perc után. Milyen eloszlást követ ekkor a mérkőzések időtartalma? Vigyázat, ha a mérkőzés hosszabbításában is gól születik, akkor a gól után a 10 perc hosszabbítás mérése automatikusan újra kezdődik.

Csak le kell fordítani a kérdésedet angolra, és jó esetben, mint most is (3. találat a google-on) meg lehet találni a választ: https://math.stackexchange.com/questions/264407/entire-function-having-simple-zero-at-the-gaussian-integers

Keresek olyan mindenhol differenciálható komplex függvényt, amelynek az összes gauss-egész a zérushelye, de csak a gauss-egészek a zérushelyei. Ha lehet, a függvényt az ismert elemi függvények segítségével és a négy alapművelet véges sokszori alkalmazásával írjuk fel. Előre is köszönöm mindenkinek a segítségét!

Mind a két megjegyzésed jogos, köszönöm!

1. Az óramutató képletem nem volt jó: 30*(t/30) helyett 30*(t/60) a jó. Így megoldva az egyenleteket kijön a 12/11 óra.

2. A külőnbség abszolut értéke egy órán belül (ha t: 0 és 60 között) kétszer lesz 110. Pontosítani kell a feladatkiírást

A két eredmény nem ugyanannyi. Az 1 óra 6 perc nem 12/11 óra. Ráadásul ma 6-tól 7-ig az órámat néztem, és a két mutató kétszer is 110 fokot zárt be egymással. Ez 110 fok helyett szinte minden szögre igaz. 7-kor 150 fokos szöget zárnak be, így nem sokkal előtte is meg kell hogy valósuljon a 110 fok. Az eredmény irányított szögek esetén tényleg ugyanannyi minden szögre.

Köszi yield, pont ilyen megoldásra vágytam, hiszen 5.-6. osztályosoknak tűzték ki.

Fapados megoldás:

I. 18 óra után

- kismutató helyzete: 180*($\displaystyle t_1$/30)

- nagymutató helyzete: 30*($\displaystyle t_1$/30) + 180

- egyenlet: kettő külőnbsége = 110

II. 19 óra után

- kismutató helyzete: 180*($\displaystyle t_2$/30)

- nagymutató helyzete: 30*($\displaystyle t_2$/30) + 210

- egyenlet: kettő külőnbsége = 110

Ebből:

- $\displaystyle t_1$ = 14 (18:14-kor volt 110 fokos a külőnbség)

- $\displaystyle t_2$ = 20 (19:20-kor volt 110 fokos a külőnbség)

Akkor feladat megoldása: (19:20 - 18:14) = 1óra 6perc.

Köszi Sirpi, de nekem egy kicsit furcsa az eredmény, hiszen fel sem használtuk, hogy a szög 110 fokos, így független lenne attól az eredmény?

Mivel a nagymutató 12-szer megy körbe, amíg a kicsi egyszer, ezért 12 óra alatt 11-szer előzi meg a nagymutató a kicsit, így 11-szer fordul elő, hogy egy adott szöget zár be egymással a két mutató (feltéve, hogy a szöget irányítottnak tekintjük). Így a válasz $\displaystyle \frac{12}{11}$ óra.

Egyébként minden órában kétszer is 110 fokot zárnak be a mutatók (egyszer a nagymutató van elől, egyszer a kicsi). Ezeknek az eseteknek a vegyes kezelése az előző egyszerű módon nem megy.

Üdv mindenkinek! Van egy egyszerű 5.-6. osztályos feladat, amire nem kapok elemi megoldást, segítenétek? Az A időpontban esti 6 óra után az óra két mutatója 110 fokos szöget zárnak be. A B időpontban esti 7 óra után ugyancsak 110 fokos szöget zárnak be. Mennyi a két időpont közötti különbség? Üdv: epsilon

Felteszek közbülső kérdéseket akkor.

A süvegek alapja kör alakú, de mekkora ennek a körnek a kerülete? Mekkora a sugara? Mekkorák a kúp alkotói (vagyis azok a szakaszok, amik a kúp csúcsát összekötik az alap egy pontjával)? Ebből mi a válasz az (a) kérdésre?

A (b) kérdéshez próbálj meg ábrát rajzolni, ami egy a kúp tengelyével párhuzamos síkra vetítve mutatja a süveget és a legnagyobb gömb alakú varázsgömböt, ami még pont befér a süveg alá. Ebből számold ki ennek a gömbnek a sugarát.

Lenne egy feladat, amihez sehogy sem tudok hozzákezdeni és a ti segítségeteket szeretném kérni. Törpilla Halloween előtt elhatározza,hogy varázsló süveget készít magának és három barátnőjének egy 64cm átmérőjű körlapból úgy,hogy a körlapból egyenlő nagyságú körcikkekre vágja. a, Határozza mrg,milyen magasak lesznek a kúp alakú süvegek? A végeredményt egészre kerekítse. b, Befér e a süveg alá Hókuszpók 14cm átmérőjű varázsgömbje, ha sikerül figyelmét elterelve a törpöknek elcsenni?

Gyorsabban: $\displaystyle 216=3*x*y*(x+y)$, innen $\displaystyle 72=u*v$, ahol $\displaystyle u=x+y$ és $\displaystyle v=x*y$, azaz $\displaystyle u|72$ és, ha $\displaystyle u,v$ adott, akkor felírható egy másodfokú egyenlet, amelynek gyökei éppen $\displaystyle x$ és $\displaystyle y$.

Próbáld meg a $\displaystyle 3x2y+3xy2$ kifejezést szorzattá alakítani úgy, hogy minden tényező az $\displaystyle x$ és $\displaystyle y$ változók egész együtthatós polinomja maradjon. Ha egész megoldásokat keresel, akkor ezeknek a tényezőknek az értéke is egész lesz, így mindegyiknek az értéke a $\displaystyle 216$ szám osztója. Ennek a számnak csak 32 osztója van, ezért így nagyon le tudod szűkíteni a lehetőségeket.

Sziasztok!
Szeretnék egy kis segítséget kérni a

$\displaystyle 216=6^{3}=3x^{2}y+3xy^{2}$

egyenlet egész megoldásainak megtalálásához. Grafikonról leolvastam
az $\displaystyle x_1=1$, $\displaystyle y_1=8$ illetve az $\displaystyle x_2=8$, $\displaystyle y_2=1$ egész megoldásokat.
Lenne olyan eljárás, amivel az egész megoldásokat megkaphatnám?
Hasonlóan, mint a sokkal egyszerűbb $\displaystyle y=1/x$ esetén.

Talán megér egy ábrát a szabályos 18-szög alapú megoldás, mert a szokásos megközelítés - háromszög körülírt köre = 18-szög körülírt köre - nem túl célravezető.

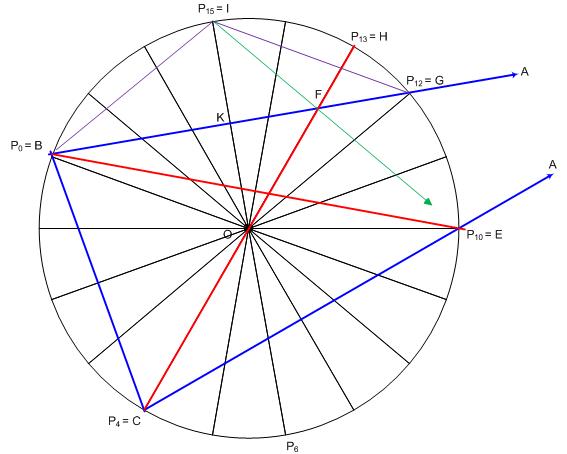
Legyenek a szabályos 18-szög csúcsai $\displaystyle P_0 … P_{17}$ , körülírt köre k, középpontja O. Helyezzük el háromszügünket úgy, hogy $\displaystyle B = P_0$ és $\displaystyle C = P_4$ legyen . k-ban a kisebb $\displaystyle P_4 P_{12}$ ívhez tartozik 80 fokos kerületi szög, így a BA egyenes áthalad $\displaystyle G= P_{12}$ -n. Hasonlóan a CA egyenes átmegy $\displaystyle P_{10}$ -en. A kisebb $\displaystyle P_4 P_{10}$ ívhez éppen 60 fokos kerületi szög tartozik, tehát $\displaystyle E = P_{10}$. Mivel a $\displaystyle P_{13} P_0$ ívhez tartozik 50 fokos kerületi szög, a CB-vel 50 fokos szöget bezáró egyenes a $\displaystyle P_4 P_{13} = CH$ átmérő, ennek metszéspontja AB-vel F. A $\displaystyle P_{12} P_{15} = GI$ és a $\displaystyle P_{15} P_0 = IB$ ívekhez 60 fokos középponti szög tartozik, OGI és IBO szabályos háromszögek, OGIB rombusz, középpontja legyen K. $\displaystyle FOK \angle = HOI \angle = P_{13} O P_{15} \angle = 40^o$. IKF és OKF egybevágó derékszögű $\displaystyle \Delta$-ek, IF egyenes OF = CF tükörképe AB-re . $\displaystyle KIF \angle = OIF \angle = P_{6}IF \angle = 40^o$. 40 fokos kerületi szög éppen a $\displaystyle P_6 P_{10}$ ívhez tartozik, IF tehát átmegy $\displaystyle P_{10}$ -en , ez feladatunk EF egyenese. A keresett $\displaystyle x = FEB \angle = IEB \angle = P_{15} P_{10} P_0 \angle = 30^o$.

geogebra téma: Lineáris fv. ábrázolása (y=mx+b).Minden rendben lenne az m és b csúszkákkal változtathatók. De nem tudom a meredekségi háromszöget beszerkeszteni. Elvileg a fv.görbére egyenest kellene rendelni és a meredekség paranccsal meg kell jelenni a kis háromszögnek.Minden próbálkozásomat szintaktikai hibával dobja vissza. Kérek segítséget.Mi az a 2-3 lépés amivel tovább tudok menni? Közben azt is tapasztaltam, hogy a függvényre tett egyenes leállítja a változtatási lehetőséget.köszönöm.nagyapa.

Ellent kell mondanom. Vonka Vilmos Úr javaslata tiszta, elemi megoldáshoz vezet, szinuszok nélkül.

Ez ugyancsak a sinx/siny=sin30∘/sin110∘ összefüggéshez vezet.

Kiindulás egy elemi megoldáshoz: tekintsd azt a $\displaystyle D$ pontot az $\displaystyle AC$ oldalon, amelyre a $\displaystyle DBC$ szög 20 fokos.

Burnside-lemma egy permutációcsoportban. Az orbitok száma megegyezik a fixpontok átlagos számával. A képlet a gyöngyfűzéseket az $\displaystyle N$-szög szimmetriái szerint sorolja fel, összeadja azok fixpontjait, és utána átlagolja $\displaystyle 2N$-nel. Az $\displaystyle A$ szám a tükrözések általi fixpontokat jelzi. Nyilván, ha van legalább két páratlan számú szín, akkor nincs tükörszimmetrikus gyöngyfűzés, stb.

Köszi w, azt hittem, hogy erre az eleminek tűnő feladatnak épp olyan elemi megoldása van, mint amilyennek tűnik, mert a sinx/siny= sina/sinb ha x+y= a+b alapján x=a és y=b következik, nehezebbnek tűnik bizonyítani mint az eredeti feladat.

Hát ez igen Csábos! Erre nem számítottam, hiszen én mind azt hittem, hogy az ismétléses permutáció képletéből kiindulva, valahogyan le lehet vezetni az általánosabb esetet bár két színű golyóra, de ezek a képletek nagyon jól tükrözik a feladat általánosításának a komplexitását. valami szakirodalmi forrásanyagot tudsz-e adni, ahol ezzel az általános problémával foglalkoznak?

Íme a képlet

Legyen $\displaystyle g_1, g_2, ..., g_k$ a különböző színű gyöngyök száma

$\displaystyle N = \sum_{i=1}^{i=k}{g_i}$

$\displaystyle \text{ Nyakláncok száma}=(A+B)/2N$

Ahol

- ha 2-nél több páratlan darabszámú szín van: A=0

- ha 2 páratlan darabszámú szín van:

$\displaystyle A =\frac{((N/2)-1)!}{\prod_{i=1}^{i=k}(\left\lfloor g_i/2\right\rfloor)!}\cdot N$

- ha 0 vagy 1 páratlan darabszámú szín van:

$\displaystyle A =\frac{(N/2)!}{\prod_{i=1}^{i=k}(\left\lfloor g_i/2\right\rfloor)!}\cdot N$

Legyenek $\displaystyle d$ a $\displaystyle g_1, g_2, ..., g_k$-k legnagyobb közös osztójának osztói

$\displaystyle B=\sum_{j|d}\frac{(N/j)!}{\prod_{i=1}^{i=k}(g_i/j)!}\cdot \varphi(j)$

Az adatok mindenképpen elegendőek, mert a megadott szögek hasonlóság erejéig meghatározzák az ábrát.

Ilyen feladatoknál mindig szokott lenni

(1.) valami kedves kreatív szerkesztés, ami a szög megsejtése után nagyon elemi megfontolásokkal vezeti le annak nagyságát (sokszor pakolnak valahova szabályos háromszöget, vagy használják, hogy egy háromszög szögfelezői egy ponton mennek át),

(2.) egy szabályos $\displaystyle 18$-szög, aminek néhány átlójának egy ponton való áthaladásával ekvivalens a feladat.

A legegyszerűbb és legkönnyebb módszer azonban (3.) a szinuszarányokkal való számolás szokott lenni. A következő képletet használjuk: ha $\displaystyle ABC$ háromszögben $\displaystyle D$ egy pont a $\displaystyle BC$ oldal belsejében, akkor

$\displaystyle \frac{BD}{DC}=\frac{AB}{AC}\cdot \frac{\sin BAD\angle}{\sin DAC\angle}.$

Ez a képlet az $\displaystyle ABD\triangle$ és $\displaystyle ACD\triangle$ szinusztételeinek leosztásából adódik.

A feladat megoldása. Mivel $\displaystyle BAC\angle = 20^\circ$, ezért $\displaystyle EB=EA$, ahonnan $\displaystyle BEF\angle=x$ és $\displaystyle FEA\angle=y$ esetén $\displaystyle x+y=140^\circ$, továbbá

$\displaystyle \frac{BF}{FA}=\frac{EB}{EA}\cdot \frac{\sin BEF\angle}{\sin FEA\angle}=\frac{\sin x}{\sin y}$

és a szinusztétel szerint

$\displaystyle \frac{BF}{FA}=\frac{CB}{CA}\cdot \frac{\sin BCF\angle}{\sin FCA\angle}=\frac{\sin 20^\circ}{\sin 80^\circ}\cdot \frac{\sin 50^\circ}{\sin 30^\circ}=\frac{\sin 20^\circ\cos 40^\circ}{4\sin 20^\circ\cos 20^\circ\cos40^\circ\cdot \frac 12}=\frac{1/2}{\cos 20^\circ}=\frac{\sin 30^\circ}{\sin 110^\circ}.$

Tehát

$\displaystyle \frac{\sin x}{\sin y}=\frac{\sin 30^\circ}{\sin 110^\circ}.$

Ebből $\displaystyle x+y=140^\circ$ miatt $\displaystyle x=30^\circ$, $\displaystyle y=110^\circ$ következik.

//Ugyanis $\displaystyle x+y=140^\circ$ feltételt rögzítve, $\displaystyle x$ növelésével, $\displaystyle y$ csökkentésével $\displaystyle \frac{\sin x}{\sin y}$ is növekszik. Ezt úgy láthatjuk, ha felveszünk egy $\displaystyle AOB\angle=140^\circ$-os szögtartományban egy $\displaystyle P$ pontot az $\displaystyle AB$ szakaszon; ekkor $\displaystyle \frac{\sin x}{\sin y}=\frac{d(P,AO)}{d(P,BO)}$, ha $\displaystyle PO$ az $\displaystyle AO$-val és $\displaystyle BO$-val rendre $\displaystyle x,y$ szöget zár be. Ha $\displaystyle x$ nő és $\displaystyle y$ csökken, $\displaystyle d(P,AO)$ nő és $\displaystyle d(P,BO)$ csökken, így az arány nő.//