| [2139] marcius8 | 2017-10-05 08:11:06 |
 JÉÉÉ!!!!!! Köszi a bizonyításokat FM! Hálám örökké üldözni fog!!!!
|
|
|
|
|
| [2135] marcius8 | 2017-10-04 19:21:54 |
 A #2134 és a #2132 bizonyítások nagyon jók, nagyon szépen köszönöm! A #2132 bizonyítás nagyon tetszik, mert analógiát teremt a derékszögű háromszög és a 120°-os háromszög között!!! Magam részéről egy terület-átdarabolós bizonyítást próbáltam keresni, de ez még eddig nem sikerült. (A derékszögű háromszögre érvényes Pitagorasz-tétel legismertebb bizonyítása úgy történik, hogy egy négyzetet kétféleképpen darabolnak fel. Euklidesz is terület-átdarabolással bizonyítja a Pitagorasz-tételt.) Szóval, ha még valaki tudna a 120°-os háromszögre vagy a 60°-os háromszögre érvényes összefüggésre egy terület-átdarabolós bizonyítást annak is nagyon hálás lennék!!!!
|
|
| [2134] Lpont | 2017-10-04 15:47:01 |
 Kedves Zoltán!
Egy lehetséges megoldás a 60 fokos háromszögre:
(1) Ha ABC egyenlő szárú, akkor szabályos is egyúttal, az állítás triviálisan igaz.
(2) Ha az oldalak páronként különböznek, akkor nyilván van kisebb és nagyobb szög is 60-nál, legyen pl. a>c>b.
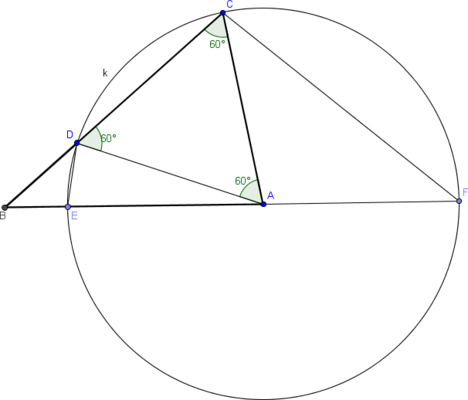
Mérjük fel b oldal hosszát rendre C-ből B felé a CB szakaszra, A-ból B-felé és vele ellentétes irányba is az az AB egyesre, kapjuk a D,E,F pontokat.
A származtatás miatt ACD szabályos, AFC és ADE egyenlő szárú háromszög. Ha A-nál lévő szög alfa, akkor F-nél alfa/2 és DAE szög alfa-60, ezért ADE szög 120-alfa/2. CDEF négyszög húrnégyszög, hiszen F-nél és D-nél lévő szögeinek összege 180.
B pontnak a húrnégyszög körülírt k körére vonatkozó hatványa: BE*BF=BD*BC, azaz (c-b)*(c+b)=(a-b)*a, ahonnan zárójelfelbontás és rendezés után a bizonyítandó állítást kapjuk.
|
 |
| Előzmény: [2131] marcius8, 2017-10-03 11:21:13 |
|
|
| [2132] Fálesz Mihály | 2017-10-04 06:11:28 |
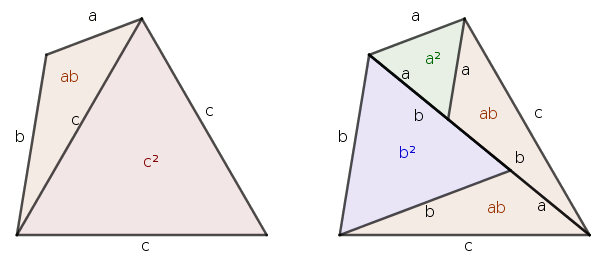
 Szerintem ez jó iskolai gyakorlat lehetne. Amikor a befogó- és a magasságtételt tanítjuk, majd a befogótételből bebizonyítjuk a Pitagorasz-tételt, fel lehet adni, hogy ezek mintájára csinálják meg a 120 fokos esetet.
A bizonyítás alapja az önhasonlóság; ha a derékszögű háromszöget kettéosztjuk az átfogóhoz tartozó magassággal, a két rész hasonló lesz az eredeti háromszöghöz.
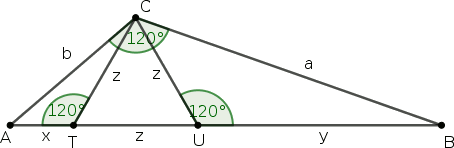
Ha a háromszög nem derékszögű, hanem van egy mondjuk 120 fokos szöge, akkor a magasság helyett belerajzolhatunk egy szabályos háromszöget. Az ábra betűzésével ABC△∼ACT△∼CBU△, és persze c=x+y+z. A hasonlóságokból
ac=ya=zb,bc=xb=zaésab=yz=zx.
Ezeket átszorozva,
a2=cy,b2=cx,ab=cz,z2=xy.
Az első kettő megfelel a befogótételnek, a harmadik a terület kétféle felírása, a negyedik a magasságtétel megfelelője. Az első hármat összeadva,
a2+ab+b2=c(x+y+z)=c2.
|
 |
| Előzmény: [2131] marcius8, 2017-10-03 11:21:13 |
|
| [2131] marcius8 | 2017-10-03 11:21:13 |
 Esetleg, ha valaki az előző hozzászólásomban említett, a 60°-os háromszögre és a 120°-os háromszögre vonatkozó összefüggéseket be tudná bizonyítani nekem a 90°-os háromszögre vonatkozó Pitagorasz-tétel felhasználása nélkül, annak nagyon hálás lennék. Vajon a Pitagorasz-tétel bizonyításához hasonlóan be lehet bizonyítani a 60°-os háromszögre és a 120°-os háromszögre vonatkozó összefüggéseket?
|
|
| [2130] marcius8 | 2017-09-29 10:03:24 |
 Geometriában az egyik legfontosabb tétel a Pitagorasz-tétel, amely szerint ha egy derékszögű háromszög befogói a és b, átfogója c, akkor a következő összefüggés teljesül:
a2+b2=c2
Ennek a tételnek a felhasználásával a következő összefüggések vezethetőek le:
Legyenek egy 60°-os háromszögnek a 60° melletti oldalai (nevezzük befogóknak) a és b, a 60°-os szöggel szemközti oldala (nevezzük átfogónak) c. Ekkor a következő összefüggés teljesül (60°-os háromszögre érvényes Pitagorasz-tétel):
a2−ab+b2=c2
Legyenek egy 120°-os háromszögnek a 120° melletti oldalai (nevezzük befogóknak) a és b, a 120°-os szöggel szemközti oldala (nevezzük átfogónak) c. Ekkor a következő összefüggés teljesül (120°-os háromszögre érvényes Pitagorasz-tétel):
a2+ab+b2=c2
A probléma a következő: Először megtanuljuk a derékszögű háromszögre a Pitagorasz-tételt, majd csak ennek felhasználásával bizonyítjuk a 60°-os háromszögre érvényes Pitagorasz-tételt, és a 120°-os háromszögre érvényes Pitagorasz-tételt. De mi lenne, ha először a 60°-os háromszögre érvényes Pitagorasz-tételt tanulnánk, és csak ennek felhasználásával hogyan kellene bizonyítani a másik két Pitagorasz-tételt? Vagy mi lenne, ha először a 120°-os háromszögre érvényes Pitagorasz-tételt tanulnánk, és csak ennek felhasználásával hogyan kellene bizonyítani a másik két Pitagorasz-tételt? Várom mindenkinek megtisztelő válaszát: Bertalan Zoltán.
|
|
| [2129] marcius8 | 2017-08-30 00:02:02 |
 Ok, teljesen igaz a megjegyzés. Akkor úgy pontosítok, hogy a mérkőzésenkénti gólok száma 3 várható értékű Poisson-eloszlást követ úgy, hogy a mérkőzés bármely viszgált időszaka alatt esett gólok száma is Poisson eloszlású. Ekkor feltehető, hogy a vizsgált időszak alatti gólok számának várható értéke úgy aránylik a teljes mérkőzés alatti gólok számának várható értékéhez, mint a vizsgált időszak hossza a teljes mérkőzés idejéhez.
|
| Előzmény: [2128] jonas, 2017-08-29 22:33:46 |
|
| [2128] jonas | 2017-08-29 22:33:46 |
 Szerintem ahhoz, hogy ezt meg lehessen mondani, nem elég annyi megkötés a modellre, hogy “A mérkőzésenkénti gólok száma Poisson-eloszlást követ”. Ha például minden jelenlegi mérkőzésnek a vége felé könnyebb gólt rúgni, mint az elején, akkor az új szabály sokszor fog hosszabbítást és több gólt eredményezni, de ettől még igaz lehet a feltételed.
|
| Előzmény: [2127] marcius8, 2017-08-29 18:16:54 |
|
| [2127] marcius8 | 2017-08-29 18:16:54 |
 Tegyük fel, hogy minden futballmérkőzés pontosan 90 percig tart, és minden mérkőzésen átlagosan 3 gól esik. A mérkőzésenkénti gólok száma Poisson-eloszlást követ. Most nagy hirtelen a nagyokos szabályalkotók összegyűlnek, és kitalálják azt az új szabályt, hogy ha akármelyik mérkőzésen egy gól esik, akkor a mérkőzés nem ér véget automatikusan 90 perc után, hanem a gól után pontosan 10 percig még tart a mérkőzés, azaz 10 perc hosszabbítás következik. Nyilván, ha az utolsó gól a mérkőzés 80.-ik perce előtt esik, akkor a mérkőzés automatikusan véget ér 90 perc után. Milyen eloszlást követ ekkor a mérkőzések időtartalma? Vigyázat, ha a mérkőzés hosszabbításában is gól születik, akkor a gól után a 10 perc hosszabbítás mérése automatikusan újra kezdődik.
|
|
|
| [2125] marcius8 | 2017-06-10 22:00:49 |
 Keresek olyan mindenhol differenciálható komplex függvényt, amelynek az összes gauss-egész a zérushelye, de csak a gauss-egészek a zérushelyei. Ha lehet, a függvényt az ismert elemi függvények segítségével és a négy alapművelet véges sokszori alkalmazásával írjuk fel. Előre is köszönöm mindenkinek a segítségét!
|
|
| [2124] yield | 2017-03-04 07:56:41 |
 Mind a két megjegyzésed jogos, köszönöm!
1. Az óramutató képletem nem volt jó: 30*(t/30) helyett 30*(t/60) a jó. Így megoldva az egyenleteket kijön a 12/11 óra.
2. A külőnbség abszolut értéke egy órán belül (ha t: 0 és 60 között) kétszer lesz 110. Pontosítani kell a feladatkiírást
|
| Előzmény: [2123] csábos, 2017-03-03 20:23:06 |
|
| [2123] csábos | 2017-03-03 20:23:06 |
 A két eredmény nem ugyanannyi. Az 1 óra 6 perc nem 12/11 óra. Ráadásul ma 6-tól 7-ig az órámat néztem, és a két mutató kétszer is 110 fokot zárt be egymással. Ez 110 fok helyett szinte minden szögre igaz. 7-kor 150 fokos szöget zárnak be, így nem sokkal előtte is meg kell hogy valósuljon a 110 fok. Az eredmény irányított szögek esetén tényleg ugyanannyi minden szögre.
|
| Előzmény: [2122] epsilon, 2017-03-03 16:19:34 |
|
|
| [2121] yield | 2017-03-03 12:06:15 |
 Fapados megoldás:
I. 18 óra után
- kismutató helyzete: 180*(t1/30)
- nagymutató helyzete: 30*(t1/30) + 180
- egyenlet: kettő külőnbsége = 110
II. 19 óra után
- kismutató helyzete: 180*(t2/30)
- nagymutató helyzete: 30*(t2/30) + 210
- egyenlet: kettő külőnbsége = 110
Ebből:
- t1 = 14 (18:14-kor volt 110 fokos a külőnbség)
- t2 = 20 (19:20-kor volt 110 fokos a külőnbség)
Akkor feladat megoldása: (19:20 - 18:14) = 1óra 6perc.
|
| Előzmény: [2120] epsilon, 2017-03-03 07:58:10 |
|
|
| [2119] Sirpi | 2017-03-02 20:44:52 |
 Mivel a nagymutató 12-szer megy körbe, amíg a kicsi egyszer, ezért 12 óra alatt 11-szer előzi meg a nagymutató a kicsit, így 11-szer fordul elő, hogy egy adott szöget zár be egymással a két mutató (feltéve, hogy a szöget irányítottnak tekintjük). Így a válasz 1211 óra.
Egyébként minden órában kétszer is 110 fokot zárnak be a mutatók (egyszer a nagymutató van elől, egyszer a kicsi). Ezeknek az eseteknek a vegyes kezelése az előző egyszerű módon nem megy.
|
| Előzmény: [2118] epsilon, 2017-03-02 18:40:48 |
|
| [2118] epsilon | 2017-03-02 18:40:48 |
 Üdv mindenkinek! Van egy egyszerű 5.-6. osztályos feladat, amire nem kapok elemi megoldást, segítenétek? Az A időpontban esti 6 óra után az óra két mutatója 110 fokos szöget zárnak be. A B időpontban esti 7 óra után ugyancsak 110 fokos szöget zárnak be. Mennyi a két időpont közötti különbség? Üdv: epsilon
|
|
| [2117] jonas | 2017-02-07 18:22:49 |
 Felteszek közbülső kérdéseket akkor.
A süvegek alapja kör alakú, de mekkora ennek a körnek a kerülete? Mekkora a sugara? Mekkorák a kúp alkotói (vagyis azok a szakaszok, amik a kúp csúcsát összekötik az alap egy pontjával)? Ebből mi a válasz az (a) kérdésre?
A (b) kérdéshez próbálj meg ábrát rajzolni, ami egy a kúp tengelyével párhuzamos síkra vetítve mutatja a süveget és a legnagyobb gömb alakú varázsgömböt, ami még pont befér a süveg alá. Ebből számold ki ennek a gömbnek a sugarát.
|
| Előzmény: [2116] Miar, 2017-02-07 17:18:22 |
|
| [2116] Miar | 2017-02-07 17:18:22 |
 Lenne egy feladat, amihez sehogy sem tudok hozzákezdeni és a ti segítségeteket szeretném kérni. Törpilla Halloween előtt elhatározza,hogy varázsló süveget készít magának és három barátnőjének egy 64cm átmérőjű körlapból úgy,hogy a körlapból egyenlő nagyságú körcikkekre vágja. a, Határozza mrg,milyen magasak lesznek a kúp alakú süvegek? A végeredményt egészre kerekítse. b, Befér e a süveg alá Hókuszpók 14cm átmérőjű varázsgömbje, ha sikerül figyelmét elterelve a törpöknek elcsenni?
|
|
|