|
| [2151] marcius8 | 2018-01-01 12:35:31 |
 Van két periodikus függvény, periódusuk aránya irracionális. Lehet-e a két függvény összege periodikus?
|
|
|
| [2149] marcius8 | 2017-12-27 11:49:04 |
 Van-e olyan 5 csúcsú poliéder, amelynek nincs 4 olyan csúcsa, amelyek egy síkban lennének, és van kívül írt gömbje, és van beírt gömbje, és van éleit érintő gömbje?
|
|
| [2148] epsilon | 2017-12-13 16:28:36 |
 Üdv mindenkinek. Segítségre lenne szükségem, mert elmerültem egy dologban. Arról van szó, hogy sin(f(x+y)=sin(f(x)+f(y)) minden x, y VALÓS számra, ahol f(x) egy valós, mindenütt folytonos függvény az R-ből az R-be. A fenti egyenletből következik-e, hogy f(x+y)=f(x)+f(y)+2nPi minden x, y VALÓS számra, vagy f(x+y)=-f(x)-f(y)+(2n+1)Pi minden x, y VALÓS számra? Vagyis továbbvíve a gondolatot, ha f folytonos, akkor az f(x+y)=f(x)+f(y)+2nPi Cauchy egyenlet összes folytonos megoldásai f(x)=ax+b alakú, továbbá az f(x+y)=-f(x)-f(y)+(2n+1)Pi egyenlet összes megoldása f(x)=kPi. A kérdés tehát: Ha sin(f(x+y)=sin(f(x)+f(y)) minden x, y VALÓS számra, f mindenütt folytonos, akkor biztosan igaz-e, hogy f(x)=ax+b, vagy f(x)=kPi? Vagy van arra ellenpélda, hogy bizonyos esetekben az egyik függvényegyenlőség igaz, más esetben a másik, de f mégis folytonos mindenütt? Nem sikerül szerkesztenem ilyen ellenpéldát. Ugyanez a kérdésem lenne cos(f(x+y)=cos(f(x)+f(y)) minden x, y VALÓS számra, ha f mindenütt folytonos. Előre is köszönöm a válaszotokat!
|
|
| [2147] Erben Péter | 2017-12-06 19:11:19 |
 Nagyon izgalmas filozófiai kérdés, hogy egy választási rendszer eredménye ,,tükrözi-e a választói akaratot” avagy a választási rendszer „igazságos-e”, de nem könnyű az ilyen kérdéseknek matematikai tartalmat adni.
Tetszőleges választási rendszer esetén általában nagyon könnyű olyan szavazat eloszlást mutatni, ami mellett az adott rendszer igazságtalannak tűnik. Ezen még az sem segít, ha előre megadjuk, milyen kritériumoknak kell megfelelnie egy választási rendszernek és csak utána próbáljuk meghatározni az eljárást. A leghíresebb ilyen negatív eredmény az Arrow-paradoxon, de sokkal egyszerűbb példával is illusztrálhatjuk a „nehéz igazságos választási rendszert csinálni” állítást.
Tegyük fel, hogy példádhoz hasonlóan listákról akarunk kiosztani M mandátumot. Induljon N párt a választáson, és az i. kapjon si szavazatot. Tegyük fel, hogy a választás eredménye az, hogy a Pi párt mi mandátumot nyert és ∑mi=M. Az egyetlen, amit szeretnénk elvárni a választási rendszertől, hogy ha si≥sj, akkor mi≥mj is igaz legyen.
Legyen most M=2, N=12, és a pártokra leadott szavazatok sorban: (2,2,1,1,1,1,1,1,1,1). Feltételünk szerint az egyetlen megengedett eredmény, hogy P1 és P2 nyer 1-1 mandátumot, a többiek pedig semmit. Ez viszont azt jelenti, hogy az aktív választók kétharmadának egyetlen képviselője sem lesz, amit nehéz igazságosnak tekinteni. Itt az „igazságtalanságot” talán inkább a mandátumok oszthatatlansága okozza, és nem valamilyen a rendszerbe beépített trükk.
A példádban említett eljárás neve d'Hondt módszer, és ez egy érdekes cikk róla. A Wikipédia szócikkben egy online kalkulátor is linkelve van, amivel lehet kísérletezgetni.
|
| Előzmény: [2145] marcius8, 2017-12-03 14:30:36 |
|
| [2146] marcius8 | 2017-12-03 16:43:13 |
 Pontosítok az előbbi hozzászólásomon: Ha valamelyik yi,j hányados valamilyen xi és valamilyen j esetén benne van az első n legnagyobb yi,j hányados között, akkor a Pi párt egy mandátumot kap. Továbbá a Pi párt annyi mandátumot kap, ahány yi,j hányados benne van az első n legnagyobb yi,j hányados között valamilyen xi és valamilyen j esetén.
|
| Előzmény: [2145] marcius8, 2017-12-03 14:30:36 |
|
| [2145] marcius8 | 2017-12-03 14:30:36 |
 Anélkül, hogy politikát hoznék a fórumba... Magyarországon az országgyűlési mandátumok egy részét úgynevezett listás választások alapján lehet megnyerni. Ez a következőképpen történik: Tegyük fel, hogy van n mandátum, és a választásokon indulnak a P1, P2, P3,.... pártok. A P1 párt kap x1 szavazatot, a P2 párt kap x2 szavazatot, a P3 párt kap x3 szavazatot,... Legyen yi,j=xi/j, ahol j egy n értékénél nem nagyobb pozitív egész szám. Az így kapott yi,j hányadosokat csökkenő sorrendbe rendezik, és meghagyják az első n legnagyobb hányadost, a többit elfelejtik. Ezek után, ha valamelyik xi esetén az yi,j hányados benne van az első n legnagyobb yi,j hányados között, akkor a Pi párt kap egy mandátumot. A mandátumok így történő szétosztása mennyiben tükrözi a választók akaratát?
|
|
|
| [2143] jonas | 2017-11-29 17:06:20 |
 Ez egy tanulságos Markov-láncos feladat, érdemes végigszámolni.
Legyen a húzások száma T. Minden 0≤t<T egészre nézzük meg, hogy t húzás után a legközelebbi húzásban hány cetli közül kell húzni, ez legyen Xt, valamint legyen Yt azon törpék száma, akik önmagukat húzzák ebben a húzásban. Tehát 0≤t<T esetén 2≤Xt≤7. Terjesszük ki az X sorozatot úgy, hogy Xt=0 ha T≤t.
Nyilván X0=7. A játék szabályai szerint ha 0≤t<T, akkor Xt+1=Yt, kivéve ha Yt=1, amely esetben Xt+1=7. Mármost rögzített Xt mellett Yt eloszlása nem függ az előzményektől. Az eloszlást pontosan meg is tudjuk adni: P(Yt=y∣Xt=x)=A008290(y,x)/x!. Itt az A008290(y, x) szám x elem azon permutációinak a száma, amiben pontosan y fixpoint van, az OEIS A008290 sorozata szerint. Ez a valószínűség nulla, ha x<y. Íme a feltételes eloszlások táblázata.
| x= | 2 | 3 | 4 | 5 | 6 | 7 |
| P(Yt=0∣Xt=x)= | 1/2 | 2/6 | 9/24 | 44/120 | 265/720 | 1854/5040 |
| P(Yt=1∣Xt=x)= | 0 | 3/6 | 8/24 | 45/120 | 264/720 | 1855/5040 |
| P(Yt=2∣Xt=x)= | 1/2 | 0 | 6/24 | 20/120 | 135/720 | 924/5040 |
| P(Yt=3∣Xt=x)= | 0 | 1/6 | 0 | 10/120 | 40/720 | 315/5040 |
| P(Yt=4∣Xt=x)= | 0 | 0 | 1/24 | 0 | 15/720 | 70/5040 |
| P(Yt=5∣Xt=x)= | 0 | 0 | 0 | 1/120 | 0 | 21/5040 |
| P(Yt=6∣Xt=x)= | 0 | 0 | 0 | 0 | 1/720 | 0 |
| P(Yt=7∣Xt=x)= | 0 | 0 | 0 | 0 | 0 | 1/5040 |
A fentiekből az is következik, hogy ha rögzítjük x-et ahol 1<x, akkor az Xt=x feltétel mellett Xt+1 eloszlása független az előzményektől, vagyis az X0,…,Xt−1 számoktól (és mellesleg még a húzott nevektől is), és ez a feltételes eloszlás bármely t-re ugyanaz. Ez azt jelenti, hogy X egy stacionáris markov lánc. Mivel Xt+1 az Yt fent leírt függvénye eloszlásból, és Yt feltételes eloszlását az előbb kiszámoltuk, ezért Xt+1 feltételes eloszlását (az átmenet valószínűségeket) is meg tudjuk adni.
| x= | 2 | 3 | 4 | 5 | 6 | 7 |
| P(Xt+1=0∣Xt=x)= | 1/2 | 2/6 | 9/24 | 44/120 | 265/720 | 1854/5040 |
| P(Xt+1=2∣Xt=x)= | 1/2 | 0 | 6/24 | 20/120 | 135/720 | 924/5040 |
| P(Xt+1=3∣Xt=x)= | 0 | 1/6 | 0 | 10/120 | 40/720 | 315/5040 |
| P(Xt+1=4∣Xt=x)= | 0 | 0 | 1/24 | 0 | 15/720 | 70/5040 |
| P(Xt+1=5∣Xt=x)= | 0 | 0 | 0 | 1/120 | 0 | 21/5040 |
| P(Xt+1=6∣Xt=x)= | 0 | 0 | 0 | 0 | 1/720 | 0 |
| P(Xt+1=7∣Xt=x)= | 0 | 3/6 | 8/24 | 45/120 | 264/720 | 1856/5040 |
Most akkor számoljuk ki T várható értékét. Erre stacionáris Markov-láncoknál a szokásos módszer a következő. Jelölje a maradék lépések számának, vagyis (T−t)-nek, a várható értékét ax az Xt=x feltétel mellett. A fentiek miatt a maradék lépések számának feltételes eloszlása is független az előzményektől, és t-től is. Nyilván a0=0. A többi (2≤x≤7) esetre felírhatunk egy-egy lineáris egyenletet a fenti átmenet valószínűségek alapján.
ax=1+∑kP(Xt+1=k∣Xt=x)⋅ak
Az egyenletrendszer megoldása után, mivel X0=7, ezért a húzások számának várható értéke a7.
A konkrét esetben az egyenletrendszer a következő.
(a2,a3,a4,a5,a6,a7)⋅(1/2−106/2420/120135/720924/504001/6−1010/12040/720315/5040001/24−1015/72070/50400001/120−1021/504000001/720−1003/68/2445/120264/7201856/5040−1)=
=(−1,−1,−1,−1,−1,−1)
Ennek a megoldása
(a2,a3,a4,a5,a6,a7)=(9713740330,13115308479,11826442740,12225059935,12123252750,12145107135)/4856870165
Így a sorsolások átlagos száma a7=12145107135/4856870165, ami körülbelül 2.50.
|
| Előzmény: [2142] marcius8, 2017-11-28 12:15:32 |
|
| [2142] marcius8 | 2017-11-28 12:15:32 |
 Igyekszem pontosabban megfogalmazni az előbbi felvetésemet. Tehát a hét törpe (Szund, Vidor, Hapci, Kuka, ....) mindegyike felírja a saját nevét egy papírra, ezeket a papírokat egy dobozkába teszik, ezután mindegyik törpe pontosan egy papírt húz a dobozkából. Ha elsőre mindenki más nevét húzza, akkor mindenki annak azt ajándékozza meg, akinek a nevét húzta. (Ennek lesz "1/e" a valószínűsége.) Ebben az esetben a "ki kit ajándékoz meg" sorsolás eredményes, és ekkor a sorsolásnak vége. Akkor van baj, ha van olyan törpe, aki a saját nevét húzta, ekkor a sorsolást a következő szabályok szerint ismétlik meg:
- Ha több, mint 1 törpe húzta a saját nevét valamelyik megismételt sorsolás esetén, akkor ezek a törpék egymás közt újra megismétlik a sorsolást.
- Ha pontosan 1 törpe húzta a nevét, akkor a sorsolást az összes törpe részvételével megismétlik, mert ez így igazságos.
- Ha valamelyik megismételt sorsolás esetén már nincs olyan törpe, aki a saját nevét húzta, akkor a sorsolás eredményes, a sorsolásnak vége, és ekkor minden törpe azt ajándékozza meg, akinek a nevét húzta.
Ekkor várhatóan hány sorsolás után lesz az, hogy minden törpe más törpének a nevét húzta?
|
| Előzmény: [2141] marcius8, 2017-11-28 09:31:52 |
|
| [2141] marcius8 | 2017-11-28 09:31:52 |
 Nemsokára itt a karácsony. A hét törpe is készül egymás megajándékozására. Ezért a hét törpe mindegyike felírja a saját nevét egy kis papírra, a papírokat összehajtva beteszik egy dobozkába. Ezután a hét törpe mindegyike húz a dobozkából pontosan egy papírt, és minden törpe annak ad ajándékot, akinek a nevét húzta. (Ebben még semmi különös nincs.) De előfordulhat, hogy lesznek olyan törpék, akik a saját nevüket húzzák (ennek durván "1/e" a valószínűsége, ami nem elhanyagolható), ezek a törpék egymás közt újra megismétlik ezt a sorsolást. Ha megint lesznek ilyen törpék, akkor ezek a törpék egymás közt újra megismétlik ezt a sorsolást.... Végül előfordulhat az is, hogy az első sorsoláskor, vagy akármelyik sorsoláskor pontosan egy törpe húzza a saját nevét, ekkor a sorsolást mind a hét törpe újra kezdi. Várhatóan hány sorsolásra kerül sor?
|
|
| [2140] marcius8 | 2017-10-08 13:47:42 |
 Nagyon jók a #2138 és #2137 bizonyítások! A 90°-os háromszögre érvényes Pitagorasz-tétel területátdarabolós bizonyításánál a terület fogalma triviálisnak tűnik. De ezek a bizonyítások arra is rávilágítanak, hogy a terület fogalma egyáltalán nem olyan triviális!!!
|
|
| [2139] marcius8 | 2017-10-05 08:11:06 |
 JÉÉÉ!!!!!! Köszi a bizonyításokat FM! Hálám örökké üldözni fog!!!!
|
|
|
|
|
| [2135] marcius8 | 2017-10-04 19:21:54 |
 A #2134 és a #2132 bizonyítások nagyon jók, nagyon szépen köszönöm! A #2132 bizonyítás nagyon tetszik, mert analógiát teremt a derékszögű háromszög és a 120°-os háromszög között!!! Magam részéről egy terület-átdarabolós bizonyítást próbáltam keresni, de ez még eddig nem sikerült. (A derékszögű háromszögre érvényes Pitagorasz-tétel legismertebb bizonyítása úgy történik, hogy egy négyzetet kétféleképpen darabolnak fel. Euklidesz is terület-átdarabolással bizonyítja a Pitagorasz-tételt.) Szóval, ha még valaki tudna a 120°-os háromszögre vagy a 60°-os háromszögre érvényes összefüggésre egy terület-átdarabolós bizonyítást annak is nagyon hálás lennék!!!!
|
|
| [2134] Lpont | 2017-10-04 15:47:01 |
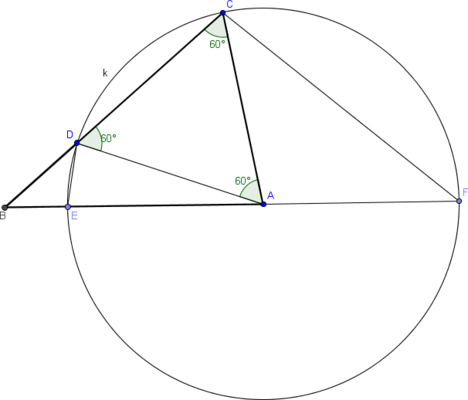
 Kedves Zoltán!
Egy lehetséges megoldás a 60 fokos háromszögre:
(1) Ha ABC egyenlő szárú, akkor szabályos is egyúttal, az állítás triviálisan igaz.
(2) Ha az oldalak páronként különböznek, akkor nyilván van kisebb és nagyobb szög is 60-nál, legyen pl. a>c>b.
Mérjük fel b oldal hosszát rendre C-ből B felé a CB szakaszra, A-ból B-felé és vele ellentétes irányba is az az AB egyesre, kapjuk a D,E,F pontokat.
A származtatás miatt ACD szabályos, AFC és ADE egyenlő szárú háromszög. Ha A-nál lévő szög alfa, akkor F-nél alfa/2 és DAE szög alfa-60, ezért ADE szög 120-alfa/2. CDEF négyszög húrnégyszög, hiszen F-nél és D-nél lévő szögeinek összege 180.
B pontnak a húrnégyszög körülírt k körére vonatkozó hatványa: BE*BF=BD*BC, azaz (c-b)*(c+b)=(a-b)*a, ahonnan zárójelfelbontás és rendezés után a bizonyítandó állítást kapjuk.
|
 |
| Előzmény: [2131] marcius8, 2017-10-03 11:21:13 |
|
|
| [2132] Fálesz Mihály | 2017-10-04 06:11:28 |
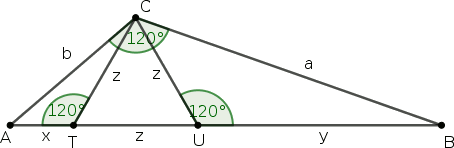
 Szerintem ez jó iskolai gyakorlat lehetne. Amikor a befogó- és a magasságtételt tanítjuk, majd a befogótételből bebizonyítjuk a Pitagorasz-tételt, fel lehet adni, hogy ezek mintájára csinálják meg a 120 fokos esetet.
A bizonyítás alapja az önhasonlóság; ha a derékszögű háromszöget kettéosztjuk az átfogóhoz tartozó magassággal, a két rész hasonló lesz az eredeti háromszöghöz.
Ha a háromszög nem derékszögű, hanem van egy mondjuk 120 fokos szöge, akkor a magasság helyett belerajzolhatunk egy szabályos háromszöget. Az ábra betűzésével ABC△∼ACT△∼CBU△, és persze c=x+y+z. A hasonlóságokból
ac=ya=zb,bc=xb=zaésab=yz=zx.
Ezeket átszorozva,
a2=cy,b2=cx,ab=cz,z2=xy.
Az első kettő megfelel a befogótételnek, a harmadik a terület kétféle felírása, a negyedik a magasságtétel megfelelője. Az első hármat összeadva,
a2+ab+b2=c(x+y+z)=c2.
|
 |
| Előzmény: [2131] marcius8, 2017-10-03 11:21:13 |
|
| [2131] marcius8 | 2017-10-03 11:21:13 |
 Esetleg, ha valaki az előző hozzászólásomban említett, a 60°-os háromszögre és a 120°-os háromszögre vonatkozó összefüggéseket be tudná bizonyítani nekem a 90°-os háromszögre vonatkozó Pitagorasz-tétel felhasználása nélkül, annak nagyon hálás lennék. Vajon a Pitagorasz-tétel bizonyításához hasonlóan be lehet bizonyítani a 60°-os háromszögre és a 120°-os háromszögre vonatkozó összefüggéseket?
|
|
| [2130] marcius8 | 2017-09-29 10:03:24 |
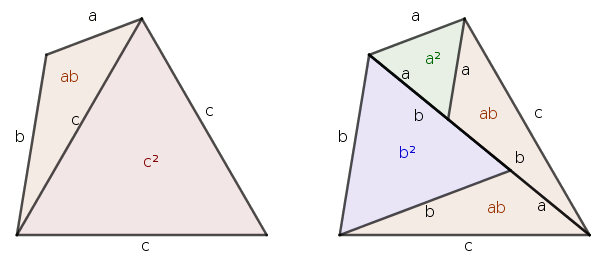
 Geometriában az egyik legfontosabb tétel a Pitagorasz-tétel, amely szerint ha egy derékszögű háromszög befogói a és b, átfogója c, akkor a következő összefüggés teljesül:
a2+b2=c2
Ennek a tételnek a felhasználásával a következő összefüggések vezethetőek le:
Legyenek egy 60°-os háromszögnek a 60° melletti oldalai (nevezzük befogóknak) a és b, a 60°-os szöggel szemközti oldala (nevezzük átfogónak) c. Ekkor a következő összefüggés teljesül (60°-os háromszögre érvényes Pitagorasz-tétel):
a2−ab+b2=c2
Legyenek egy 120°-os háromszögnek a 120° melletti oldalai (nevezzük befogóknak) a és b, a 120°-os szöggel szemközti oldala (nevezzük átfogónak) c. Ekkor a következő összefüggés teljesül (120°-os háromszögre érvényes Pitagorasz-tétel):
a2+ab+b2=c2
A probléma a következő: Először megtanuljuk a derékszögű háromszögre a Pitagorasz-tételt, majd csak ennek felhasználásával bizonyítjuk a 60°-os háromszögre érvényes Pitagorasz-tételt, és a 120°-os háromszögre érvényes Pitagorasz-tételt. De mi lenne, ha először a 60°-os háromszögre érvényes Pitagorasz-tételt tanulnánk, és csak ennek felhasználásával hogyan kellene bizonyítani a másik két Pitagorasz-tételt? Vagy mi lenne, ha először a 120°-os háromszögre érvényes Pitagorasz-tételt tanulnánk, és csak ennek felhasználásával hogyan kellene bizonyítani a másik két Pitagorasz-tételt? Várom mindenkinek megtisztelő válaszát: Bertalan Zoltán.
|
|
| [2129] marcius8 | 2017-08-30 00:02:02 |
 Ok, teljesen igaz a megjegyzés. Akkor úgy pontosítok, hogy a mérkőzésenkénti gólok száma 3 várható értékű Poisson-eloszlást követ úgy, hogy a mérkőzés bármely viszgált időszaka alatt esett gólok száma is Poisson eloszlású. Ekkor feltehető, hogy a vizsgált időszak alatti gólok számának várható értéke úgy aránylik a teljes mérkőzés alatti gólok számának várható értékéhez, mint a vizsgált időszak hossza a teljes mérkőzés idejéhez.
|
| Előzmény: [2128] jonas, 2017-08-29 22:33:46 |
|
| [2128] jonas | 2017-08-29 22:33:46 |
 Szerintem ahhoz, hogy ezt meg lehessen mondani, nem elég annyi megkötés a modellre, hogy “A mérkőzésenkénti gólok száma Poisson-eloszlást követ”. Ha például minden jelenlegi mérkőzésnek a vége felé könnyebb gólt rúgni, mint az elején, akkor az új szabály sokszor fog hosszabbítást és több gólt eredményezni, de ettől még igaz lehet a feltételed.
|
| Előzmény: [2127] marcius8, 2017-08-29 18:16:54 |
|