Fórum: Valaki mondja meg!

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93]

Szeretnél hozzászólni? Jelentkezz be.

[283] nemtommegoldani	2008-02-13 18:35:00
Az előbbi hozzászólásomhoz még egy feladatot elfelejtettem: Határozd meg a 2 az ötödiken3a negyediken7 a harmadikon*11 a tizenegyediken pozitív osztóinak számát! Köszönöm szépen!

[282] nemtommegoldani	2008-02-13 18:15:16
Újabb feladattal bombázok! Mutassa meg, hogy minden n term. szám esetén az n négyzet+3n+3 és n+1 relatív prímek! Ismét csak köszönetet tudok mondani annak a kedves embernek, aki ezt megfejti nekem.

[281] nadorp	2008-02-11 22:26:25
Természetesen igazad van, de a célom pont az volt, amit Rizsesz leírt, ti. az ax+by=c diofantikus egyenletet pont így oldjuk meg euklideszi algoritmussal. Én csak egyszerűen behelyettesítettem az általános képletekbe a konkrét értékeket. Szerintem a példát pont azért adták fel, hogy numerikusan is megértsék a bizonyítást, ezért volt az én levezetésem annyira "szájbarágós".
Előzmény: [279] BohnerGéza, 2008-02-11 16:50:13

[280] rizsesz

2008-02-11 16:58:27

Itt pont az volt a lényeg, hogy az általános módszert végigvezessük ezen a konkrét eseten, ami akkor is működik, ha az ax+by=c egyenletben a és b relatív prímek. Itt egy olyan esettel álltunk szemben, ahol nem voltak azok, de maga a módszer természetesen ilyenkor is működőképes.

Ha az ember csak meg akarja oldani, és látja, hogy egyszerű, akkor persze fejben kitalálja a megoldást.

Előzmény: [279] BohnerGéza, 2008-02-11 16:50:13

[279] BohnerGéza	2008-02-11 16:50:13
Ha eleve egyszerűsítem 7-tel?!
Előzmény: [278] nadorp, 2008-02-11 13:18:54

[278] nadorp

2008-02-11 13:18:54

98=77^.1+21

77=21^.3+14

21=14^.1+7

14=7^.2+0

Innen a lnko=7.

Az első egyeneletből

21=98-77^.1

A második egyeneletből felhasználva az elsőt

14=77-21^.3=77-(98-77^.1)^.3=77^.4-98^.3.

Tehát egy megoldás az x=-3 y=-4, azaz az általános megoldás

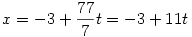
$x=-3+\frac{77}7t=-3+11t$

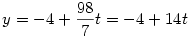
$y=-4+\frac{98}7t=-4+14t$

Előzmény: [277] nemtommegoldani, 2008-02-10 22:43:59

[277] nemtommegoldani

2008-02-10 22:43:59

Oldjuk meg a következő diofantikus egyenletet:98x-77y=14 a megadott módon: euklideszi algoritmussal adja meg lnko-t, majd ennek a segítségével adja meg az összes megoldást! A feladatot már megoldottam más módszerrel, de az euklideszi algor. segítségével nem uazt az eredményt kaptam, mint a másiknál. Az jó megoldás, de nem fogadják el, mert az euklideszi algoritmust kellene hozzá használni. Mit téveszthettem az euklideszi algoritmusnál? Köszönöm a választ.

[276] lorantfy	2008-02-01 19:22:54
Szia Csocsi! Most kaptam kölcsön egy hasonló játékot, de ez csak 6 db-os. Szerintem azért segíteni fog Neked, ha jársz még erre.

Előzmény: [179] csocsi, 2007-03-22 19:53:56

[275] epsilon	2008-01-17 06:50:31
Igen, olvasom, az valóban az, de ami a [264] nadorp hozzászólás első felében van, az nem pont az, csak annak a segítségével (olyan típusú egyenlőtlenségek összegezésével) bizonyítják a Cebisev egyenlőtlenséget.

[274] sakkmath	2008-01-16 16:47:31
Az angol szakirodalomban így hívják: Chebyshev Sum Inequality. Klikk ide.
Előzmény: [269] epsilon, 2008-01-16 12:31:07

[273] epsilon	2008-01-16 14:26:36
Bocs: ehelyett a1×b1+a2×b2>=a1×b2+a2×b2 ez kell a1×b1+a2×b2>=a1×b2+a2×b1

[272] epsilon

2008-01-16 14:25:10

OK, valóban így is lehet nézni, de akkor a rendezési tételt valójában nagyágyúnak használjuk hiszen n=2 esetén b2>=b1 és a2>=a1 feltételek mellett egyetlen nemtriviális permutációra van bizonyítanivaló egyenlőtlenség: a1×b1+a2×b2>=a1×b2+a2×b2 ami átírva (b2-b1)×(a2-a1)>=0 és vágül nincs szükség a nagyágyúra, mert végső soron csak az ai illetve bi rendezését vesszük figyelembe, de vehetjük úgy is, hogy az ötletet a rendezési tétel adta. Üdv: epsilon

[271] nadorp

2008-01-16 13:04:13

Ha jobban megnézed, minden lépésben használtam n=2-re.

$\frac{xy}z+\frac{pq}r\geq\frac{xy}r+\frac{pq}z$ , ha xy $\leq$ pq és z>r

Előzmény: [270] epsilon, 2008-01-16 12:35:53

[270] epsilon	2008-01-16 12:35:53
u.i.: Én úgy vélem, hogy a bizonyítás során végül is nem igazán használtad a "rendezési tételt" hanem inkább az a1<=a2<=...<=an rendezést, mert Én őszintén bevallva nem látom, hogy a rendezési tételből melyek a 264. hozzászólás kezdetén levő ai illetve bi azonos monotonítású sorozatok. Vagy tévedek? Üdv: epsilon

[269] epsilon	2008-01-16 12:31:07
Kedves nadorp! A "Tulajdonképpen az a2 nevezőt "toljuk el" mindig 1-gyel balra" pontosításod úgy nézem, teljesen eloszlatja a kételyeimet, mégegyszer tüzetesen levezetek több első és utolsó lépést. Kedves sakkmath! Kösz az infót, ott is szétnézek, de megköszönném, ha be tudnád szkennerelni, és gondolom, könnyebb ha valahova feltöltöd és a linket megadod hogy letölthessük(gondolom, nem szabályellenes), mert itt méretkorlát is van a képekre. Üdv: epsilon
Előzmény: [267] nadorp, 2008-01-16 10:21:56

[268] sakkmath

2008-01-16 11:10:24

Kedves epsilon és nadorp!

Az 'ujjgyakorlatok' topic [273]-as hozzászólásában Sirpi dióhéjban elmondja a Szűcs-féle rendezési tételt (egy konkrét feladat megoldása kapcsán). Sirpi ismertetéséből is látható, hogy az a bizonyítás, amibe bekapcsolódtam, a Szűcs Adolf-féle rendezési tételt használja.

Csebisev nevéhez többféle egyenlőtlenség is fűződik. A jelen témakörhöz legközelebbi egyenlőtlensége megtalálható Skljarszkij-Csencov-Jaglom: Válogatott fejezetek és tételek... 1. kötetében (TipoTex Kiadó) is. Ha kell, holnapra kiollózom és fölteszem. Üdvözlettel: sakkmath

Előzmény: [263] epsilon, 2008-01-15 15:20:39

[267] nadorp

2008-01-16 10:21:56

A két utolsó tört a második esetben:

$\frac{a_{n-2}a_{n-1}}{a_n}$ és $\frac{a_{n-1}a_n}{a_2}$

A két utolsó tört a harmadik esetben:

$\frac{a_{n-3}a_{n-2}}{a_{n-1}}$ és $\frac{a_{n-2}a_{n-1}}{a_2}$

Tulajdonképpen az a₂ nevezőt "toljuk el" mindig 1-gyel balra

Előzmény: [266] epsilon, 2008-01-16 09:01:10

[266] epsilon

2008-01-16 09:01:10

Helló nadorp! Belenéztem jobban a bizonyításba, és úgy tűnik, hogy a második lépéstől lefele az első lépésben elsütött minorálás nem igazán alkalmazható? Pontosabban: ott ahol írod, hogy "Kezdjük a végén az utolsó két taggal, ekkor"...itt a nevezőkben ebben a sorrendben a1 és a2 szerepel, és a1<a2. Ellenben ahol ezt írod, hogy "Újra a fenti "rendezési tételt" alkalmazva a két utolsó törtre" ott a nevezőben ebben a sorrendben a3 és a2 szerepek és ezekre a3>a2 vagyis úgy látom, hogy nem teljesül a rendezési tételből a monotonítási feltétel, és ugyanez a helyzet tovább lefele minden más 2 összehasonlításnál szerintem éppen a fordított egyenlőtlenség miatt úgy vélem, nem ismételhető meg az 1. lépés, vagy tévedek? Üdv: epsilon

[265] epsilon

2008-01-16 06:47:02

Helló! Köszi nadorp! A jobboldali egyenlőtlenséget Én is úgy tudtam, hogy a Cebisev nevéhez fűződik, hiszen annak a bizonyítsa során ilyen típusú egyenlőtlenségeket alkalmazunk, találkozunk. Az általánosítási ötletedben végül a mentő ötlet az volt, hogy lépésről-lépésre alkalmaztad, Én azért jártam zsákutcába, mert egyből akartam alkalmazni a jobboldali egyenlőtlenséget (vagy a Cebisevet), de akárhogy választottam a tagokat, vagy nem lehetett tudni semmit az egymáshoz való viszonyukról, vagy a sorozatok ellentétes nonotonításuak voltak, így nem járhattam sikerrel. Tüzetesen átnézem a bizoyítást, de már a gondolatmenetet követve nagyon egyértelműnek tűnik, hogy így kell lenie. Üdv: epsilon

[264] nadorp

2008-01-15 20:48:41

Sajnos a "Szűcs rendezési tételt" nem olvastam, de gyanakszom, hogy a következőtől nem áll messze. Egyébként ezt anal gyakon vettük és úgy tudtam, hogy ez a Csebisev-egyenlőtlenség :-( pedig tényleg nem az.

Legyenek a₁ $\leq$ a₂ $\leq$ ... $\leq$ a_n és b₁ $\leq$ b₂ $\leq$ ... $\leq$ b_n nemnegatív számok. Ekkor, ha a {c_i} számok a b_i számok egy tetszőleges permutációja, akkor

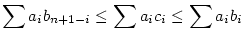$\sum a_ib_{n+1-i}\leq\sum a_ic_i\leq\sum a_ib_i$ .

Ha ezt felhasználjuk, akkor igaz az eredeti feladat következő általánosítása ( hacsak megint nem néztem el valahol egy egyszerűsítést :-)

Legyenek a₁ $\leq$ a₂ $\leq$ ... $\leq$ a_n (n $\geq$ 3) pozitív számok. Ekkor

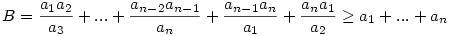
$B=\frac{a_1a_2}{a_3}+...+\frac{a_{n-2}a_{n-1}}{a_n}+ \frac{a_{n-1}a_n}{a_1}+\frac{a_na_1}{a_2}\geq a_1+...+a_n$

Kezdjük a végén az utolsó két taggal, ekkor

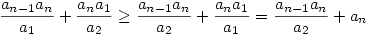$\frac{a_{n-1}a_n}{a_1}+\frac{a_na_1}{a_2}\geq \frac{a_{n-1}a_n}{a_2}+\frac{a_na_1}{a_1}= \frac{a_{n-1}a_n}{a_2}+a_n$ . Tehát

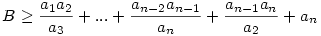
$B\geq \frac{a_1a_2}{a_3}+...+\frac{a_{n-2}a_{n-1}}{a_n}+ \frac{a_{n-1}a_n}{a_2}+a_n$

Újra a fenti "rendezési tételt" alkalmazva a két utolsó törtre

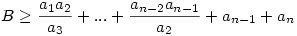
$B\geq \frac{a_1a_2}{a_3}+...+ \frac{a_{n-2}a_{n-1}}{a_2}+a_{n-1}+a_n$

Ezt folytatva, előbb utóbb ezt kapjuk

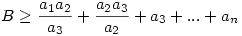
$B\geq \frac{a_1a_2}{a_3}+\frac{a_2a_3}{a_2}+a_3+...+a_n$

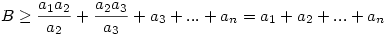
$B\geq \frac{a_1a_2}{a_2}+\frac{a_2a_3}{a_3}+a_3+...+a_n= a_1+a_2+...+a_n$

Előzmény: [263] epsilon, 2008-01-15 15:20:39

[263] epsilon	2008-01-15 15:20:39
Köszi sakkmath a javítást (örömömben észre sem vettem a végén az elírást), na meg kösz a szakreferenciát. Mivel nem jutok hozzá ahoz a forráshoz amit írtál, megfogalmaznád a Szűcs-tételt? Tisztelettel üdv: epsilon

[262] nadorp	2008-01-13 20:30:54
Köszi a javítást, igazad van. Belezavarodtam a sok betűbe :-)
Előzmény: [261] sakkmath, 2008-01-13 16:18:31

[261] sakkmath	2008-01-13 16:18:31
Kedves nadorp!

Előzmény: [258] nadorp, 2008-01-08 11:29:29

[260] epsilon	2008-01-12 08:58:36
Helló nadorp! A feladat 5 vagy több tag esetén is igaznak tűnik, de a 4-re adott bizonyítást sok eset letárgyalása nélkül nem igazán látom átültetni pl 5 tagra :-( Van valami ötleted? Üdv: epsilon
Előzmény: [258] nadorp, 2008-01-08 11:29:29

[259] epsilon	2008-01-08 15:02:50
Helló! Köszi, jó ötlet volt az, hogy azt az 1 törtet ami nem illett bele a Cebisev egyenlőtlenségbe (a rendezés monotonításába), 2 esetbe véve tárgyaltad, így valóban teljesen logikus, szép megoldás! Üdv: epsilon

Már regisztráltál?
Új vendég vagy?