| [324] epsilon | 2008-03-03 18:51:57 |
 Kedves Lajos! Az a=0 és a=1 értékek esetén a 2 tagra alkalmazott Jensen-féle egyenlőtlenség valóban megadja az f konvexitását, kösz a hozzászólásod ahol írtad! Most már csak az a furcsa, mint írtam, hogy ezekben az esetekben is fennáll az, hogy az x=0 ill. x=1 esetekben nem teljesül a 2a-1=2a+1, vagyis a deriváltal=érintőmeghúzhatósággal való gond továbbra is homályosít? Mi a valódi helyzet, miért van ez a látszólagos ellentmondás? Mert azzak, hogy e 2 pontban konvex, még nem zárja ki, hogy más ban ne lenne az!? Üdv: epsilon
|
|
| [323] epsilon | 2008-03-03 18:26:27 |
 Kedves Lajos! Örvendek, hogy megint jelentkeztél, mert továbbra is érdekelne a 297-es feladat tisztázása (ezúttal nem írtam el), vagyis, hogy miért edták arra azt a választ, hogy PONTOSAN 2 olyan "a" érték van amelyre az konvex lenne. Mint láttuk, az x=a-ban nem deriválható, viszont Te meg írod a 302-ben, hogy az a=0 és a=1 esetben konvex, bocs de Én nem látom miért, mert ebben a 2 esetben is fennáll a már említett 2a-1=2a+1 absurdum, ami az a pontban való deriválhatóság származtat.(vagyis nem húzható az érintő, és ebben a pontban nem érvényes a konvexitás jelzett értelmezése!?) Üdv: epsilon
|
|
|
| [321] epsilon | 2008-03-03 17:56:23 |
 Huh a rézangyalát! Elnézést kérek Mindenkitől! Annyira bele vagyok merülve ebbe meg az ilyen típusú csapdás feladatokba, hogy egy 2-es hatványkitevőt elhagytam, amire egyébként a megoldásaimat is leírtam, tehát elnézéseteket kérve a rekurzió HELYESEN:
|
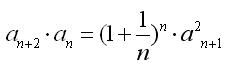 |
|
|
| [319] Lóczi Lajos | 2008-03-03 17:02:01 |
 "aránypárok tulajdonságát használtam, és az a(n+2) alá hoztam az egyik a(n+1)-et, és a jobboldalon a nevezőbe vittem az ottmaradt a(n+1) alá az a(n)-et."
Összesen csak 1 db an+1 van, ha azt átviszed a bal oldalra, a jobb oldalon nem marad már meg!
|
| Előzmény: [316] epsilon, 2008-03-03 16:23:32 |
|
| [318] epsilon | 2008-03-03 16:47:46 |
 Tehát mégegyszer: a lehetséges válaszokból (valami hibás gondolatmenet folytán?) kihozható a limesz értékének a 0, az 1 az e akármylike, de egyik sem jó (az e és 0-át mutattam, hogy kijöhetne de nem jó válasz, az 1-et Te hoztad ki, még nem látom miért, az sem a jó válasz). Az eredmény végtelen sem lehet, tehát a "más válasz" alapján a felsoroltakon kívül van a helyes eredmény.
|
|
| [317] Lóczi Lajos | 2008-03-03 16:41:31 |
 "és ezek szerint akkor mégis miért állhat a jelzett válasz, hogy pont 2 a érték van amelyre konvex?"
Ha a=0 vagy a=1, akkor a töréspont a [0,1] intervallum végpontja, és a törésponttól balra és jobbra, külön-külön, a függvény eleve konvex: a konvexitással probléma csak akkor van, amikor a töréspont a [0,1] intervallum belsejébe kerül.
|
| Előzmény: [307] epsilon, 2008-03-02 06:48:08 |
|
| [316] epsilon | 2008-03-03 16:23:32 |
 Helló nadorp! Ne haragudj, de többvalami elkerülte a figyelmedet: 1) Lennebb beidézem a kiinduló feladatot, és ott meglátod miről van szó! 2) A rekurzióban teljesen mindegy, hogy n-et vagy k-t írunk, nem de? 3) Az aránypárok tulajdonságát használtam, és az a(n+2) alá hoztam az egyik a(n+1)-et, és a jobboldalon a nevezőbe vittem az ottmaradt a(n+1) alá az a(n)-et. 4) Ha tehát a(n+1)/a(n) a jobboldalon b(n)-el lett jelölve, akkor a baloldalon a(n+2)/a(n+1) egyértelműen b(n+1). Aztán a teljes rekurziót átírtam n helyett k-ra, és az (1+1/k)-nek az k-adik hatványát e(k)-val jelöltem, és a kapot, általad beidézett rekurzió szerintem teljesen igaz. 5) Az általad kihozott 0 erdménysajnos 101 százalékban HIBÁS, a feladatnál jeleztem, hogy melyik a helyes válasz, a könyvet majdnem mind ilyen feladatokkal állították össze, sok minden látszatra úgy tűnik, hogy jó, de a helyes válasz nem az. Ismételem, a helyes válasz az (E) erre mérget lehet venni, íme mégegyszer a feladat, és kösz, hogy foglalkozol vele. Még van egy pár tucat ilyen, feladat, ami látszatra másnak tűnik, mint ami a helyes válasz! Üdv: epsilon.
|
 |
|
| [315] nadorp | 2008-03-03 11:21:29 |
 Ne haragudj, de szerintem már a kiindulási új rekurzió is rossz. Nem értem, hogy jött ki a bk+1=ek.bk
Különben, ha 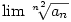 létezik, akkor az csak 1 lehet, ui. a rekurzióból létezik, akkor az csak 1 lehet, ui. a rekurzióból

Tehát 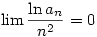
|
| Előzmény: [312] epsilon, 2008-03-02 08:52:36 |
|
| [314] epsilon | 2008-03-02 09:15:39 |
 Vajon ez már jó megoldás lenne:
|
 |
|
| [313] epsilon | 2008-03-02 08:53:27 |
 A p>=2 helyett k>=2 kell ( a képben már nem javítottam ki)
|
|
| [312] epsilon | 2008-03-02 08:52:36 |
 Keves Lajos! Más irányból közelítettem meg a feladatot, és az kiderült, hogy a két kezdetérték nem befolyásolja a limeszt:
|
 |
|
| [311] epsilon | 2008-03-02 07:59:00 |
 A 304-es hsz kapcsán: ha egy limeszt többféle képpen helyesen számolunk ki, akkor nem lehet különböző eredménye, de nagyon negéz eldönteni, hogy most a többféle eredmény alapján azért a "más válasz" a helyes, mert többféle eremény jött ki helyesen? vagy ??? Azzal egyetértek, hogy a kezdetértékek befolyásolják a limeszt, éppen ezért az eredeti rekurziót logaritmáltam, így egy 2-ik rendű nemhomogén rekurzió jött létre, a homogén egyenletnek dupla gyöke van, valóban a kezdetértékek bennemaradnak a szokásos 2 paraméter meghatározásában, de egyenlőre még az ebből adódó limesz kiszámolásával, nem jutottam dűlőre. Más ötletem az volt, hogy a b(n)-ben levő rekurzióban, lévén, hogy egymásutáni tagokról van szó (a két oldalon), összeszorozva, az a(n) sorozat általános tagját megkaptam, de az L kiszámolásával elakadtam :-( Szóval eléggé ingoványos talajokra is jutottam. üdv: epsilon
|
|
| [310] epsilon | 2008-03-02 07:53:16 |
 Megint más, noha látható, hogy a b(n) sorozat növekvő, és limesze nem lehet 0:
|
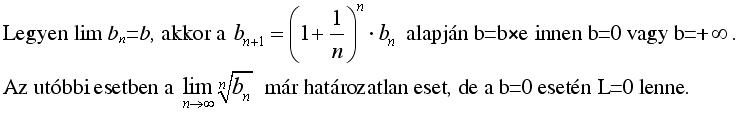 |
|
| [309] epsilon | 2008-03-02 07:48:39 |
 Ugyancsak ez jön ki a következő képpen, ha S-C és a (*) együttes alkalmazását végzem, de itt a "részleges határértékre térés" szerintem már nem mondható (?)
|
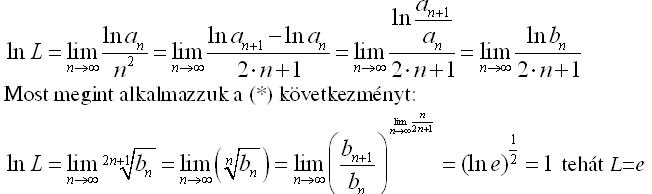 |
|
| [308] epsilon | 2008-03-02 07:38:15 |
 Helló! Mivel csak MathType-ban dolgozok, és a képlopóval a képek mérete meghaladja a megengedettet, ezért részletekben írok. A legtöbb valószínűséggel a határértéknek az e értéket tulasdonítanám, noha a következő bizonyításban a "részleges határértékre térés" vitatott lehet, ami miatt az eredmény is.
|
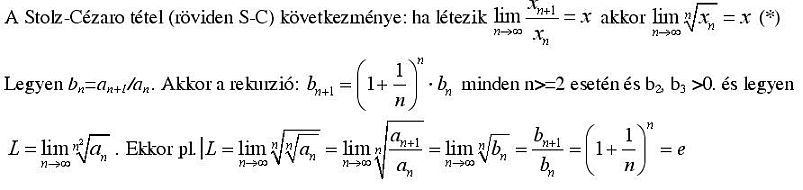 |
|
| [307] epsilon | 2008-03-02 06:48:08 |
 Kedves Lajos! Teljesen egyetértek a 305-ös észrevételeddel, éppen a 2a-1=2a+1 absurdum jött ki (amikor a deriválhatóságot említettem), és ezek szerint akkor mégis miért állhat a jelzett válasz, hogy pont 2 a érték van amelyre konvex? Természetesen MINDEN feladat esetén PONTOSAN 1 válasz helyes, és az biztosan helyes. A 304-es észrevételedre és eredményeimre visszatérek, megírom a saját számolásaimat, mert túl szép, és érdekesnek tűnik az egész feladat. Kösz, hogy foglalkoztál vele! Üdv: epsilon
|
| Előzmény: [305] Lóczi Lajos, 2008-03-02 00:45:31 |
|
|
| [305] Lóczi Lajos | 2008-03-02 00:45:31 |
 Ha a (0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex. (0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex.
|
| Előzmény: [303] epsilon, 2008-03-01 21:28:00 |
|
| [304] Lóczi Lajos | 2008-03-01 23:49:03 |
 Az A-E-s tesztben ugye csak 1 helyes megoldást karikázhatunk be? (Számolás nélkül) azt gondoltam, hogy az a2, a3 kezdőértékek alkalmas megválasztásával többféle limesz is kihozható, tehát a végeredmény nem egyértelmű, ezért E. Te milyen lehetséges értékekek kapsz?
|
| Előzmény: [303] epsilon, 2008-03-01 21:28:00 |
|
| [303] epsilon | 2008-03-01 21:28:00 |
 Köszi Lajos! 1) A 297 feladat esetén azért gondoltam a deriváltra, mert egyik értelmezése az alulról konvexnek az, hogy a [0,1] intervallumon a függvény bármely pontjában húzott érintő a függvény ábra alatt van. és a derivált mértani jelentése alapján arra is gondoltam.Az a=0 és a=1 valóban az, de a helyes válasz az, hogy PONTOSAN 2 megoldás, tehát maradna, miért nincs más "a" érték? 2)A 298 esetén nem értem a kérdve kifejtett "válaszod", szóval ott a megoldókulcs alapján az (E) a helyes, de ...mint írtam, Én ki tudok hozni eredményeket a nem helyesek kötül, és...nem látom a tévedést, tehát érdekelne: MIÉRT az (E) válasz a helyes? Vagyis mi a helyzet azzal a limesszel, mennyi, vagy nem létezik? 3) A 299 esetén Én néztem el a válasznak megjelölt betűt! Üdv: epsilon
|
| Előzmény: [302] Lóczi Lajos, 2008-03-01 19:30:01 |
|
|
|
|



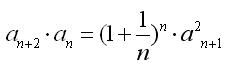




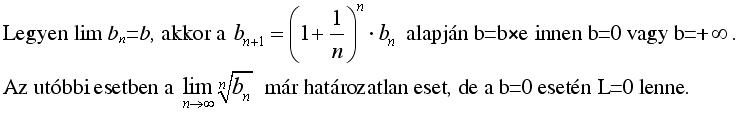
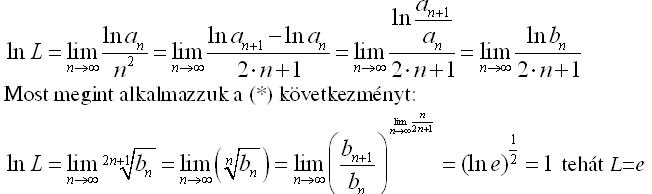
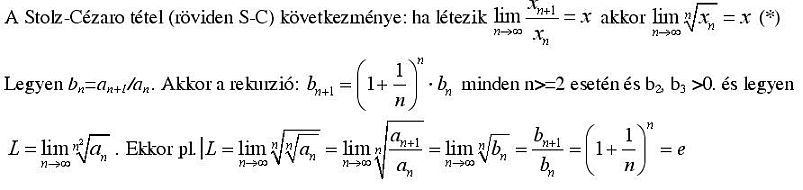
 (0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex.
(0,1) a nyílt intervallumban van, akkor f nem deriválható x=a-ban, mert a két félérintő különböző szöget zár be: a balérintő meredeksége 2a+1, míg a jobbérintőé 2a-1. A balérintő mindig pozitív meredekségű és meredekebb, mint a jobbérintő. A függvény tehát nem lehet konvex. [an+b]
[an+b]