|
| [487] epsilon | 2008-04-28 09:50:50 |
 A 734. meglett :-) , szép feladat!
|
|
| [486] epsilon | 2008-04-27 10:37:40 |
 Helló!Megint gyűltek keményebb feladatok, a következő integrálok esetén sorra valahol belefulladtam, vagy regény lett a megoldásból :-( ha Valakinek van valami örlete, előre is köszönöm! Üdv: epsilon
|
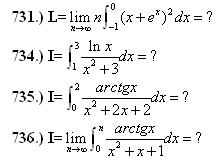 |
|
| [485] epsilon | 2008-04-25 14:30:03 |
 Hát akkor ezek szerint, a több mint 1000 feladatot tartalmazó könyvből kb ez a 3. hibás (hiányos megfogalmazásu,) feladat.
|
|
| [484] nadorp | 2008-04-24 09:52:46 |
 Ekkor Doom megoldását általánosítva k<m<n pozitív egészekre a
qn-(4k+1)qm+(5m-n)qk+(4k-5m+n)=0
egyenletnek kell keresni az összes q 1 valós megoldását. Kérdés, hogy mindig van-e? 1 valós megoldását. Kérdés, hogy mindig van-e?
Pld. k=1 m=2 n=4 esetén q2+2q-2=0 vagy
k=1 m=3 n=5 esetén q3+2q2-2q-6=0
|
| Előzmény: [483] epsilon, 2008-04-23 15:54:54 |
|
| [483] epsilon | 2008-04-23 15:54:54 |
 Helló Doom! Úgy fordítottam, és ez alapján úgy értem, hogy mindkét sorozatból összeadjuk pl. az m-edik, n-edik, p-edik, s-edik tagokat, ahol az m, n, p, s nem föltétlen egymás utáni számok.
|
| Előzmény: [482] Doom, 2008-04-23 15:32:13 |
|
|
| [481] epsilon | 2008-04-23 14:47:55 |
 Helló Doom és Csimby!A feladat fordításból származik, többször is átnéztem, de SEHOL sem ír arról, hogy EGYMÁSUTÁNI tagok lennének, úgy írja, hogy 4 azonos (egyforma) sorszámú (indexű) tagok páronkénti öszegéről van szó! Sajnos ebben az esetben nem látom be a Káli gúla szép megoldásában, hogy az úgy lenne :-( és olyan kár lenne érte :-(
|
| Előzmény: [473] Doom, 2008-04-22 07:31:52 |
|
| [480] Sirpi | 2008-04-23 11:20:34 |
 Köszi a válaszokat! Akkor nem is agyalok tovább rajta :-)
|
|
| [479] HoA | 2008-04-22 17:54:24 |
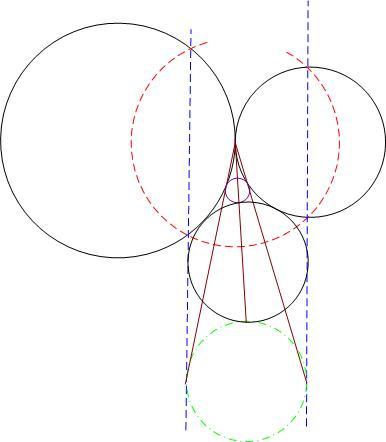
 Én is. De ha már lerajzoltam, felteszem a szerkesztés megoldását. Inverzióval egyszerű. Legyen az inverzió középpontja a két nagyobb - ha van - kör ( k1 és k2 ) érintési pontja, alapköre pedig a harmadik körre ( k3 )merőleges. ( piros kör ). Ekkor k3 inverze önmaga, a másik kettőé két párhuzamos, k3-at érintő egyenes (kék) . A szerkesztendő kör inverze érinti k3-t és a két egyenest (zöld). A szerkesztendő érintési pontokat a zöld kör érintési pontjainak az inverzió középpontjából történő vetítésével kapjuk (barna egyenesek).
|
 |
| Előzmény: [478] jonas, 2008-04-22 16:41:19 |
|
|
|
|
| [475] Sirpi | 2008-04-22 14:55:52 |
 Egy probléma (nem tudom a megoldást, sőt azt se, hogy mennyire nehéz, csak eszembe jutott): Ha egy r1, r2 és r3 sugarú kör páronként kívülről érinti egymást (3 kül. pontban), akkor ki lehet a három sugárral fejezni az őket a) kívülről b) belülről érintő kör sugarát? Esetleg szerkeszthetők a középpontok?
|
|
| [474] Csimby | 2008-04-22 14:34:09 |
 Ha a "megfelelő" nem egymás utánit jelent, akkor ez a megállapítás semilyen plusz információt nem adna, hiszen pl. bármely 4 természetes szám egy számtani sorozat megfelelő indexű tagja (1,2,3,... - számtani sorozaté).
|
|
| [473] Doom | 2008-04-22 07:31:52 |
 Szia! Pont ezért nem szívlelem a "megfelelő" szót, mert mindenki mást érthet alatta. Visszagondolva középiskolás éveimre, mi úgy tanultuk, hogy ez kb az "egymás utáni, sorrendben" kifejezésekkel azonos, bár láthatod hogy először én is bizonytalan voltam ebben. Ha azonban elfogadjuk, akkor az is feltehető hogy a 18, 18, 26, 58 úgy van megadva, hogy az első, második, harmdik, negyedik tagok összege ennyi ("megfelelő" sorrendben :)).
Próbálkoztam a teljesen általános megoldással is (nem egymás utáni tagok pl.), de akkor túl sok az ismeretlen egy egyértelmű megoldáshoz.
Ui: a (4)es egyenletbe sajtóhiba csúszott, az természetesen 40-nel egyenlő és nem pedig 8-cal - Javítottam (Sirpi).
|
| Előzmény: [471] epsilon, 2008-04-22 06:46:59 |
|
| [471] epsilon | 2008-04-22 06:46:59 |
 Helló Doom! Az elkezdését Én is így próbáltam, de nem mertem egyértelműen az a+b=18 összefüggést felírni, hiszen negatív rációk esetén, nem biztos, hogy ez az összeg kell adja a legkisebb eredményt, vagy tévedek? Üdv: epsilon
|
| Előzmény: [472] Doom, 2008-04-21 22:22:32 |
|
| [470] epsilon | 2008-04-22 06:44:24 |
 Huh de szép megoldások! Kösz szépen Mindkettőtöknek! Üdv: epsilon
|
|
|
| [468] Káli gúla | 2008-04-22 00:17:37 |
 Felhasználhatjuk, hogy egy q hányadosú mértani sorozat különbségi sorozata is q hányadosú mértani sorozat. Alkalmazzuk ezt kétszer az összeg sorozatra. Ezt lehet tagonként, ezért a számtani sorozat rész eltűnik, és az összeg második differenciáinak hányadosa az eredeti mértani sorozat hányadosa lesz:
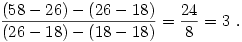
|
| Előzmény: [465] epsilon, 2008-04-21 20:09:49 |
|
| [472] Doom | 2008-04-21 22:22:32 |
 Ugyanis ekkor, ha a két sorozat:
a, a+d, a+2d, a+3d és b, b*q, b*q2, b*q3
akkor felírhatjuk a következő összefüggéseket:
a+d+b*q=a+b+d+b*(q-1)=18-ba behelyettesítve (1)-et:
| d+b(q-1)=0 -> b(q-1)=-d | (2) |
Továbbá a+2d+b*q2=a+b+2d+b(q2-1)=26-ba beírva (1)-et és felbontva a zárójelet:
2d+b(q-1)(q+1)=8
ebbe beírva (2)-t:
| 2d-d(q+1)=d(2-q-1)=d(1-q)=8 | (3) |
Továbbá a+3d+b*q3=a+b+3d+b(q3-1)=58-ba beírva (1)-et és felbontva a zárójelet:
3d+b(q-1)(q2+q+1)=40
ebbe beírva (2)-t:
| 3d-d(q2+q+1)=d(3-q2-q-1)=d(2-q2-q)=40 | (4) |
Most vegyük (3)/(4)-et, ahol d-vel tudunk egyszerűsíteni, ugyanis d nem lehet 0, különben se (3), se (4) nem teljesülne. Ekkor:
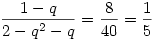
5-5q=2-q2-q
q2-4q+3=0
Megoldva ezt a másodfokú egyenletet q1=3, ekkor d=-4 illetve q1=1, ekkor (3) alapján d*(1-1)=d*0=8 ami ellentmondás.
Tehát (ha az előző hozzászólásomban lévő feltételekkel élünk) az egyedüli megoldás a mértani sorozat hányadosára q=3
|
| Előzmény: [465] epsilon, 2008-04-21 20:09:49 |
|
| [467] Doom | 2008-04-21 21:39:29 |
 Ehhez te feltetted, hogy egymást követő elemekről van szó? Vagy a "megfelelő" pont ezt jelentené? Csak mert ez nagyban leegyszerűsítené a feladatot... :)
|
| Előzmény: [466] S.Ákos, 2008-04-21 20:58:08 |
|
|
| [465] epsilon | 2008-04-21 20:09:49 |
 Helló! Megint találtam egy K.O. feladatot: Egy számtani és egy mértani sorozat 4 megfelelő indexü tagjait páronként összeadva, a 18, 18, 26, 58 számokat kapjuk. Mennyi a mértani sorozat állandó hányadosa? Van-e valakinek valami tippje? Előre is köszönöm! Üdv: epsilon
|
|
|




 , ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.
, ráadásul az integrál se nehéz, hiszen csak az e2x-et, x.ex-et és x2-et kell hozzá integrálni, egyikkel sincs gond.
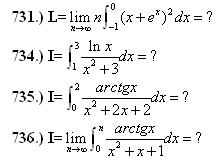
 1 valós megoldását. Kérdés, hogy mindig van-e?
1 valós megoldását. Kérdés, hogy mindig van-e? 






