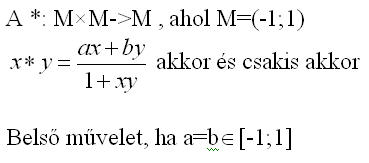| [538] nadorp | 2008-05-23 07:54:54 |
 Tudom, hogy a példa már történelem :-), de itt egy közvetlen levezetés.
Legyen 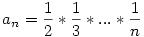
Ekkor 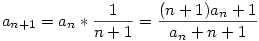 , így , így
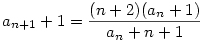 és és
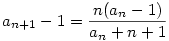 tehát tehát
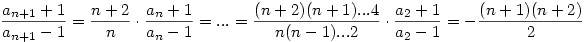
Innen 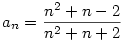 , ami persze azonos Sirpiével. , ami persze azonos Sirpiével.
|
|
|
|
|
| [534] Sirpi | 2008-05-20 23:51:25 |
 Ja, végül is ez tényleg megmagyarázza :-)
A -1-re megvolt a sima tangens, +1-re meg a feladat miatt megnéztem külön, aztán általánosan is. Bevallom, rég volt szükségem a th addiciós képletére...
|
| Előzmény: [533] jonas, 2008-05-20 23:45:11 |
|
|
|
|
|
|
| [528] Káli gúla | 2008-05-20 16:37:30 |
 Az persze kérdés, hogy ki mit tekint logikus vagy nyilvánvaló dolognak. Lehet, hogy sok embert éppen a logika téveszt meg a 0-val kapcsolatban:
(1) Valaminek a fele mindig kisebb, mint maga a valami (feleakkora). (2) A 0-nál nincs kisebb. (3) Tehát a 0-nak nincsen fele.
Logikusnak tűnik. (Azt hiszem, Arisztotelész mondta, hogy a nehezebb test nyilvánvalóan gyorsabban esik, mint a könnyebb. Galilei adott egy gyönyörű indirekt bizonyítást arra, hogy ez nem igaz.)
|
| Előzmény: [526] rizsesz, 2008-05-20 15:53:28 |
|
| [527] Csimby | 2008-05-20 15:58:38 |
 Én úgy emlékszem általános iskolában nem volt se páros, se páratlan. Egyetmen páros. Gimiben is páros. De hogy a 0 természetes szám-e, az előadónként változik :-)
|
|
| [526] rizsesz | 2008-05-20 15:53:28 |
 A -400 pedig nem egy racionális szám négyzete... Szerintem a matematika egy abszolút logikus dolog, ahogyan az már korábban kiderült, pl. a 11-szög szerkesztéses témában. Szerintem nincsen értelme arról beszélni, hogy a 0 páros-e, mert abszolúte nyilvánvalóan az, akármelyik szabály szerint is vizsgáljuk. Hasonló ez ahhoz a kérdéshez, hogy 0 természetes szám-e (itt már csak a kicsit szofisztikált "ha nem lenne az, akkor a pozitív egész szám elnevezésnek nem lenne értelme" indoklás győtött meg engem a megállapodásokon túl :))
|
| Előzmény: [525] BohnerGéza, 2008-05-20 15:23:16 |
|
|
|
|
| [522] Sirpi | 2008-05-20 08:08:14 |
 Gondolom a plusz jelek helyett is csillagokat kell érteni.
Teljes indukcióval könnyen igazolható az állítás, nevezetesen:
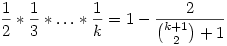
Ha k=2, akkor 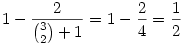 , tehát az állítás igaz. , tehát az állítás igaz.
Most bizonyítsuk k-1-ről k-ra:
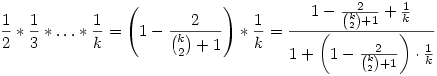
Bővítsünk a két nevező szorzatával:
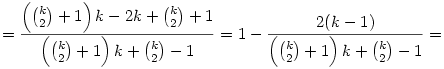
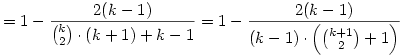
Itt (k-1)-gyel lehet egyszerűsíteni, és be is bizonyítottuk az állítást.
|
| Előzmény: [519] epsilon, 2008-05-19 20:24:41 |
|
|
| [520] dadika | 2008-05-19 22:07:26 |
 Köszönöm a választ.
Igen, minden oldalról közelítve párosnak tűnik. Nekem viszont egyszer egy tanár azt mondta, hogy se nem páros, se nem páratlan(lehet, hogy rosszul emlékszek) A matek szóbeli tételnél jött elő, nem a rulettre gondoltam.
|
| Előzmény: [513] SmallPotato, 2008-05-19 13:58:23 |
|
| [519] epsilon | 2008-05-19 20:24:41 |
 Helló! Még van egy szaporátlan feladat, jó lenne valami szabály ennek az elvégzésére! Előre is kösz, üdv: epsilon
|
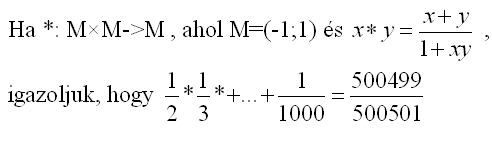 |
|
|
| [517] epsilon | 2008-05-19 18:23:43 |
 Helló! Köszi Káli gúla! Valóban, így még ha "határérték szagja" is van, de meg lehet "lobbyzni"! ;-) Üdv: epsilon
|
|
|
| [515] epsilon | 2008-05-19 15:57:41 |
 Pontosabban az a gondom vele, hogyaz a=b egyenlőséget limesszel tudtam bizonyítani. Vázolom: legyen x=1-1/n és y=-1+1/n. Ezeket beírva a * műveletve, a határárték [-1;1] közöt kellene legyen, ellenben a tört nevezője a 0-hoz tart, a számláló pedig (a-b)-hez, így véges határérték csak a 0/0 határozatlan esetből adódhat. Tehát szükséges, hogy a=b legyen. Tényleg nem jönne össze analízis nélkül? Üdv: epsilon
|
|
| [514] epsilon | 2008-05-19 15:49:58 |
 Helló! Megint akadt egy látszatra könnyű feladat,bármilyen ötletet szívesen várok! Előre is kösz, epsilon
|
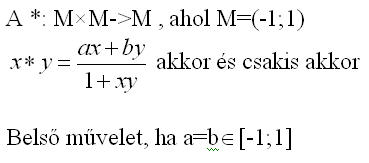 |
|




 =1/c2. Akkor innen ismerhettem ezt a képletet.
=1/c2. Akkor innen ismerhettem ezt a képletet. 
 összeadásba) megy át.
összeadásba) megy át. 
 R művelet, amit úgy definiálunk, hogy
R művelet, amit úgy definiálunk, hogy 


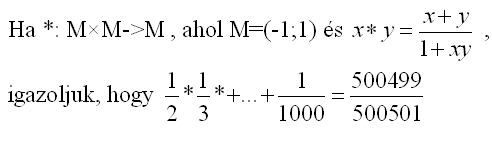
 (0,1), akkor a=b. Szorozd meg (1-x2)-tel: |a-b|x<1-x2. Ez csak úgy lehet, ha |a-b|=0. Persze el lehet mondani határértékkel is, de egyszerűbb lerajzolni.
(0,1), akkor a=b. Szorozd meg (1-x2)-tel: |a-b|x<1-x2. Ez csak úgy lehet, ha |a-b|=0. Persze el lehet mondani határértékkel is, de egyszerűbb lerajzolni.