| [629] Róbert Gida | 2008-10-06 22:51:05 |
 Nem írtad, de feltételezem, hogy T a természetes egészeken van értelmezve, így a,b 0-t is feltehetem. 0-t is feltehetem.
1. eset: a+b<1. Tetszőleges N0 egészre és elég nagy d számra telejesül, hogy T(n) d*n minden n<N0-ra. Legyen most d*n minden n<N0-ra. Legyen most 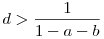 és még olyan nagy, hogy az előbbi feltétel is teljesül, azaz T(n)<d*n, ha n<N0 és még olyan nagy, hogy az előbbi feltétel is teljesül, azaz T(n)<d*n, ha n<N0
Indukcióval tegyük fel, hogy k<n-re T(k) d*k. Ekkor k=n-re is teljesül ez: a feltételt használva: T(n) d*k. Ekkor k=n-re is teljesül ez: a feltételt használva: T(n) n+T(an)+T(bn) n+T(an)+T(bn) n+adn+bdn=(1+d(a+b))n n+adn+bdn=(1+d(a+b))n dn teljesül, mert d(1-a-b)>1 igaz, d-re tett feltevés miatt. dn teljesül, mert d(1-a-b)>1 igaz, d-re tett feltevés miatt.
2. eset: Ha a+b>1, akkor létezik olyan c>1 valós szám, melyre T(n)=nc-vel definiált sorozat esetén T teljesíti a feltételt, továbbá T nyilván nem lineáris (mert c>1). c egyébként az a szám, melyre, ha a,b<1, akkor ac+bc=1 teljesül, ha a 1 vagy b 1 vagy b 1, akkor tetszőleges c>1 jó. 1, akkor tetszőleges c>1 jó.
3. eset Ha a+b=1, ekkor nem tudom mi van.
|
| Előzmény: [623] Algo, 2008-10-06 16:51:21 |
|
| [628] Doom | 2008-10-06 22:47:36 |
 Szia!
Igen, jól gondolkodsz. Annyi megjegyzést fűznék hozzá, hogy figyeld meg a Fibonacci sorozat kialakulását, ez még sokszor jól jöhet...
|
| Előzmény: [627] Algo, 2008-10-06 21:09:15 |
|
| [627] Algo | 2008-10-06 21:09:15 |
 Kedves Jonas és Doom!
A feladat ismertetése előtt 2-es számrendszerben próbáltam felírni a számokat, s ehhez társítani az optimális pénzmennyiséget. Ötleteteket végiggondoltam, s valóban 8 Ft felhasználásával meg tudom mondani, melyik számra gondolt. Egyfajta önmagamat is meggyőzésképpen: 1Ft---> 1 szám 2FT---> 2 szám 3Ft---> 3 szám 4Ft---> 5 szám 5Ft---> 8 szám 6Ft---> 13 szám 7Ft---> 21 szám 8Ft---> 34 szám
A megfelelő pénzek esetén visszavezetjük egy korábbi estre(pl.: 6Ft-ra úgy jön a 13 szám, hogy 8-5 arányban osztjuk szét, s 8 számhoz pedig legfeljebb 5 Ft-ra van szükségem)
Még egyszer köszönöm Jonasnak és Doomnak, hogy ötletüket megosztották.
Üdv.:Algo
Ui.: Remélem helyes a gondolatmenetem.:)
|
|
|
| [625] Doom | 2008-10-06 20:18:23 |
 Szia!
1-eshez egy kis segítség: gondold úgy végig, hogy n forint hány számra elég? Például 1 ft-ból 1 számból tudod kitalálni a megfelelőt, 2 forintból már 2-ből, 3 ft-ból 3-ból, 4-ből már 5 szám közül... és itt megállnék, mert lelőném a poént. :P Ha így se megy, akkor adok még segítséget, de jobb lenne magadtól rájönni.
|
| Előzmény: [623] Algo, 2008-10-06 16:51:21 |
|
|
| [623] Algo | 2008-10-06 16:51:21 |
 Sziasztok! Íme 2 feladat amivel nem tudok mit kezdeni:
1,Jancsi gondolt egy számra 1 és 32 között. Barchobával kell kitalálni a számot. Jani az igen válaszokért 1 Ft-ot, míg a nem válaszokért 2 Ft-ot kér. Legkevesebb hány Ft-ra lesz szükségünk a szám kitalálásához? Személy szerint 9 Ft-ig jutottam, de tudom hogy nem ez az optimális.
2, Milyen a,b számokra kapunk lineáris becslést a T(n)<=n+T(an)+T(bn) rekurzióból?
Aki meg tudja mondani, annak nagyon szépen megköszönném. Sajnos rengeteget foglalkoztam velük, de nem tudtam mit kezdeni velük. Várom válaszotokat. Előre is köszönöm.
Üdv.:Algp
|
|
| [622] Ali | 2008-10-06 10:37:09 |
 Nem azt akartad írni, hogy
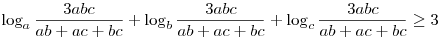
, mert az is igaz ?
A biz. ahogy Jónás elkezdte, utána kihasználni hogy log fv. konkáv, végül pedig a harmonikus és számtani közép közti egyenlőtlenség.
|
| Előzmény: [620] S.Ákos, 2008-10-05 21:37:26 |
|
|
| [620] S.Ákos | 2008-10-05 21:37:26 |
 Sziasztok! Oktv-n régebben szerepelt a következő egyenlőtlenség, amivel nem tudtam semmit kezdeni. Bbe, hogy 0<a,b,c<1 esetén
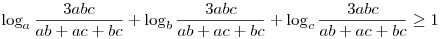
Tudnátok segíteni?
|
|
|
|
|
| [616] petya108 | 2008-10-05 19:09:35 |
 Sziasztok! Most regiszráltam magam a pontversenybe (interneten). Azt szeretném kérdezni, hogy az újságban lévő "Nevezési Lap"-ot is be kell küldenem vagy ennyi elég volt? Válaszotokat előre is köszönöm.
|
|
| [613] Doom | 2008-09-30 17:10:27 |
 Feltehetően szabadesés, azaz v0=0 m/s, a = g = 9,81 m/s2 =  10 m/s2, t=2.5 s. Ekkor: v=a*t, s=v*t=a*t2. Ebből remélem már te is ki tudod számolni. 10 m/s2, t=2.5 s. Ekkor: v=a*t, s=v*t=a*t2. Ebből remélem már te is ki tudod számolni.
|
| Előzmény: [612] mami, 2008-09-30 13:14:12 |
|
| [612] mami | 2008-09-30 13:14:12 |
 Egy virágcserép az erkélyről 2.5 másodperc alatt esik le.Milyen magasról és mekkora sebességgel ér földet?
|
|
| [611] Doom | 2008-09-29 23:10:53 |
 Mert a jég térfogata nagyobb, mint az azonos tömegű vízé (azaz sűrűsége kisebb), így mikor megfagy, kitágul. Mivel a kupak általában jól rá van csavarva, így nem enged, ezért az üveg reped szét, hogy helyet adjon a jégnek.
|
| Előzmény: [610] Dorottya, 2008-09-29 19:15:49 |
|
| [610] Dorottya | 2008-09-29 19:15:49 |
 Valaki segítsen nekem! A vizesüveg miért reped szét hogyha lefagyasztom??? Sürgős lenne!!! Előre is köszike a segítségeteket!!!!!!
|
|
| [609] jenei.attila | 2008-09-29 13:24:48 |
 Természetesen ilyen 12-es futamot nem választ, sőt olyat sem, hogy akár csak egy hatos is szerepelt volna már eddig kiválasztott futamban. Ezt az biztosítja, hogy a kiválasztandó 12-es (vagy kisebb) futamot az összes eddig kiválasztottal összevetjük, és csak akkor fogadjuk el, ha mindegyikkel legfeljebb 5 közös eleme van. Ha bármelyik már kiválasztottal legalább 6 közös eleme van, akkor folytatjuk a keresést, méghozzá a csökkenő sorrendű súlyú versenyzőkön lexikografikusan tovább haladva (vagyis a nem megfelelő futam legkisebb súlyú versenyzője helyett a következő kisebb súlyút véve, sít.). Ilyen módod minden hatos kiválasztás csak egy 12-es futamban szerepelhet. A program pedig akkor áll le, ha az összes súly 0 (0 súlyú elemet soha nem választunk ki). Ez egyben azt is jelenti, hogy minden hatos kiválasztás szerepel valamelyik 12-es (vagy kisebb) futamban, hiszen egy versenyző súlya jelenti azt, hogy hány, még futamba nem sorolt hatosban szerepel. A súlyok minden futam kiválasztáskor csökkennek, méghozzá lehetőleg a nagy súlyok. Vagyis előbb-utóbb minden versenyző súlya 0 lesz.
|
| Előzmény: [608] jonas, 2008-09-29 12:24:32 |
|
|
| [607] jenei.attila | 2008-09-28 20:11:57 |
 Végülis van egy nem használt gépem, de a programom még ránézésre is elég ronda, minimális erőfeszítéssel csiszolható. Egyébként az algoritmus rendkívül egyszerű: felveszek egy 45 elemű tömböt, amely tartalmazza, hogy az adott indexű elem még hány olyan 6-os kombinációban szerepel, amiket a már kiválasztott 12-es (vagy kevesebb elemet tartalmazó) osztályok nem generálnak (legyen ez az adott elem súlya; kezdetben az összes elem súlya 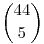 ). Pl. a tömb 1. eleme jelzi, hogy az 1-es szám még hány osztályozatlan 6-os kombinációban szerepel (ez az 1 súlya). Ezután az elemek csökkenő súlyának sorrendjében (tehát elsősorban nehéz elemeket választva) lexikografikusan generálom a 12-es kombinációkat egészen addig, amíg a kiválasztott 12-es (vagy kisebb) osztály a már kiválasztottak mindegyikével legfeljebb 5 közös elemet tartalmaz (ez biztosítja, hogy egy 6-os kombinációt csak egy osztály generál). Ha a megfelelő osztály kiválasztatott, akkor az említett tömbben a kiválasztott elemek súlyát annyival csökkentjük, ahány új 6-os kombinációban szerepel az illető elem. Az egész eljárást addig folytatjuk, amíg a súlyok mind 0-ák nem lesznek. A súly tömböt egyébként minden sikeres kiválasztás után csökkenőleg rendezem. ). Pl. a tömb 1. eleme jelzi, hogy az 1-es szám még hány osztályozatlan 6-os kombinációban szerepel (ez az 1 súlya). Ezután az elemek csökkenő súlyának sorrendjében (tehát elsősorban nehéz elemeket választva) lexikografikusan generálom a 12-es kombinációkat egészen addig, amíg a kiválasztott 12-es (vagy kisebb) osztály a már kiválasztottak mindegyikével legfeljebb 5 közös elemet tartalmaz (ez biztosítja, hogy egy 6-os kombinációt csak egy osztály generál). Ha a megfelelő osztály kiválasztatott, akkor az említett tömbben a kiválasztott elemek súlyát annyival csökkentjük, ahány új 6-os kombinációban szerepel az illető elem. Az egész eljárást addig folytatjuk, amíg a súlyok mind 0-ák nem lesznek. A súly tömböt egyébként minden sikeres kiválasztás után csökkenőleg rendezem.
|
| Előzmény: [606] jonas, 2008-09-28 18:44:16 |
|
|
|
|
|



 0-t is feltehetem.
0-t is feltehetem.  d*n minden n<N0-ra. Legyen most
d*n minden n<N0-ra. Legyen most 




 10 m/s2, t=2.5 s. Ekkor: v=a*t, s=v*t=a*t2. Ebből remélem már te is ki tudod számolni.
10 m/s2, t=2.5 s. Ekkor: v=a*t, s=v*t=a*t2. Ebből remélem már te is ki tudod számolni.