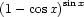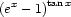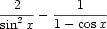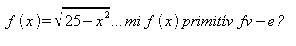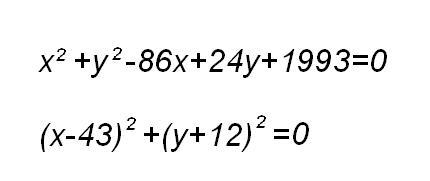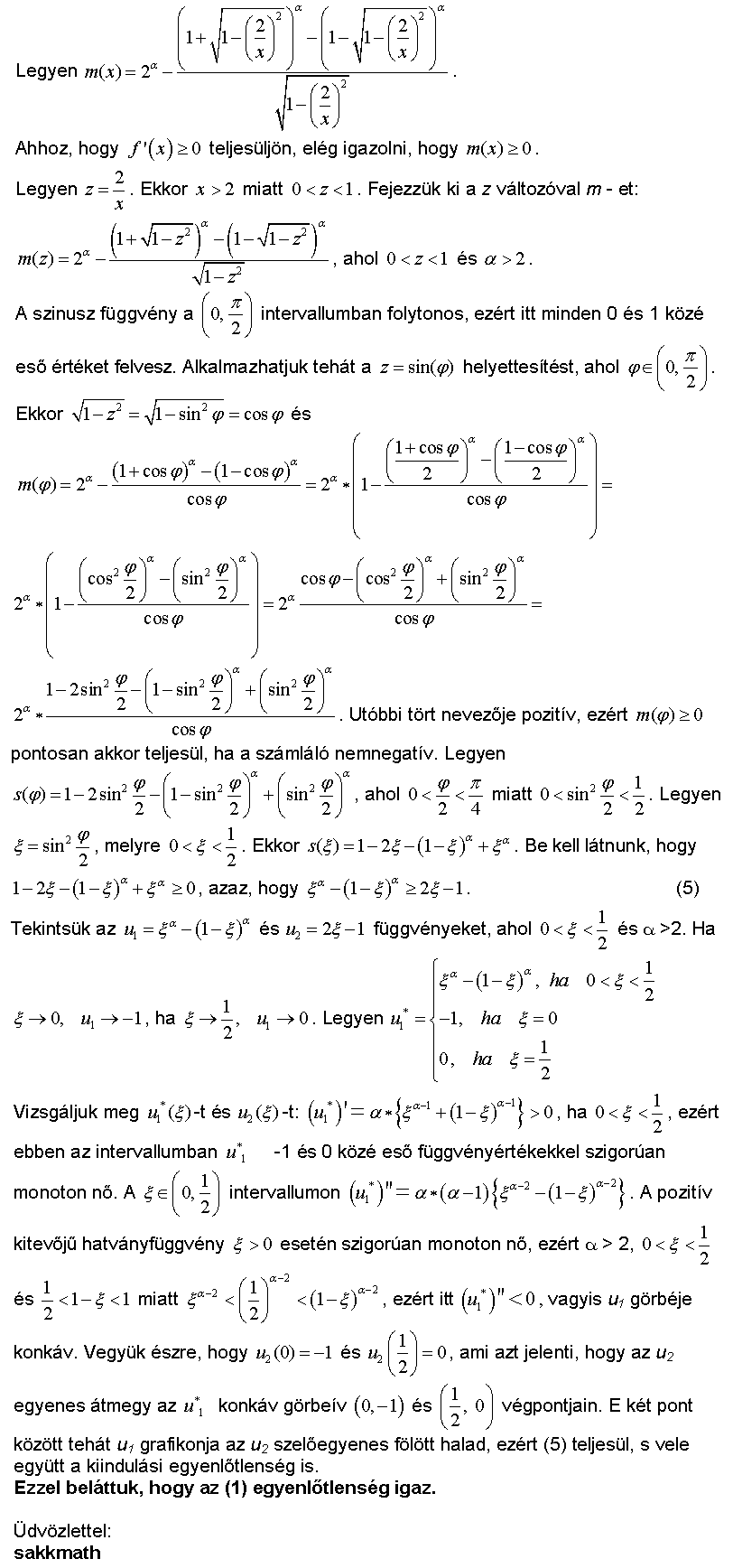|
| [677] sandor720 | 2008-11-16 20:53:59 |
 szia!
köszönöm a segítséget volna még kettő feladat. 1 feladat x 0+0
|
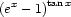 |
|
| [676] sandor720 | 2008-11-16 19:50:45 |
 Szia!
Euler gondolom erre gondoltál:2tgx/1/tg2x-re
|
|
| [675] Euler | 2008-11-16 18:10:42 |
 Gondolom a határérték a 0-ban kell, hiszen ott izgalmas a dolog.Használd a sinusra vonatkozó kétszeres szögfüggvényt, majd ezt ird be az első tag nevezőjébe, ezek után használd a kétszeres szög cosinusára vonatkozó összefüggést, ezt ird be a második tag nevezőjébe, hozz közös nevezőre, majd használd a trigonometrikus Pitagorasz tételt a számlálóban, a keresett határértk 1/2 lesz. Remélem érthető volt, amit leirtam és tudod használni.
|
| Előzmény: [674] sandor720, 2008-11-16 10:30:59 |
|
| [674] sandor720 | 2008-11-16 10:30:59 |
 Sziasztok!
függvény határérték szamitáshoz kérném segitségeteket. Ezt a feladatott nem tudom levezetni
|
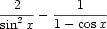 |
|
| [673] Rochard | 2008-11-09 20:17:15 |
 Köszönöm! Nagy segítség! Így nem megy ezzel tovább az időm.
|
|
|
|
| [670] Rochard | 2008-11-09 18:29:24 |
 Sziasztok!
Valaki meg tudja mondani, hogy igaz-e a következő egyenlőtlenség? És ha igen, akkor hogyan lehetne bizonyítani?
![\forall x\in R, \forall n\in N_+: \frac{[nx]}{n} \le \frac{[(n+1)x]}{(n+1)}](keplet.cgi?k=E6AA4B5B8E48C40F)
ahol [x]: x egész része.
Előre is köszönöm! Üdv!
Rochard
|
|
| [669] Kemény Legény | 2008-11-09 14:08:44 |
 Pontosan ugyan nem tudom lefordítani a mondatot, de a "median-duality" annak a transzformációnak a leírása, hogy egy háromszögből elkészítjük a súlyvonalai által alkotott háromszöget. A mondat lényegi jelentése: "Elkészítve egy tetszőleges ABC háromszögből a súlyvonalai által alkotott háromszöget..."
Ha szóról szóra le akarod fordítani: "súlyvonal-dualitás" lenne, de ha csak ahhoz kell, hogy megértsd a cikket, akkor a fenti körülírás elég.
Mellesleg mindez pl. arra használható, hogy egy általános háromszögben teljesülő összefüggést átírhass a belőle képzett súlyvonal-háromszögre, annak ugyanis az oldalai az eredeti súlyvonalak lesznek, a súlyvonalai pedig az eredeti oldalak 3/4-szeresei lesznek. /ez már valóban olyan "dualitás"-jellegű dolog/
|
| Előzmény: [660] S.Ákos, 2008-11-05 20:56:50 |
|
| [668] Timár Máté | 2008-11-08 13:12:50 |
 köszönöm szépen,kedves Alma,és Csimby...
|
|
| [667] Alma | 2008-11-08 11:07:15 |
 Most reggel megnéztem papíron, hogy az én módszeremmel is kijön-e ez, és megkaptam, tehát helyesnek tűnik.
Egyébként, ha valakinek esetleg nem lenne meg a Mathematica program és primitív függvényt keres, akkor annak ajánlom a http://integrals.wolfram.com oldalt.
|
| Előzmény: [666] Csimby, 2008-11-08 02:07:42 |
|
|
| [665] Alma | 2008-11-08 00:36:03 |
 Szia!
Először is 5öt hozz ki a gyök alól, hogy a 25ből 1 legyen. Ezután ajánlom az x/5 == sin(y) változóhelyettesítést. Ez azért is előnyös, mert dx/dy=5*cos(y) lesz. A végén majd cos(y)*cos(y)-t kell majd y szerint integrálnod ha jól nézem, ezt pedig megteheted például addíciós tétel alkalmazása után (kétszeres szög koszinusza alapján)
Elsőre nekem ez ugrott be. Ez alapján már szerintem nem nehéz meghatározni.
|
| Előzmény: [664] Timár Máté, 2008-11-07 23:51:01 |
|
| [664] Timár Máté | 2008-11-07 23:51:01 |
 Sziasztok! Valaki meg tudja nekem mondani hogy ha...
|
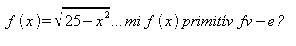 |
|
| [663] RRichi | 2008-11-06 22:42:44 |
 Az arcus cosinus (acos, arccos) függvény szolgál ennek megadására, számológépeken cos-1 -ként jelölik. Ha a működésére vagy kíváncsi, ajánlom a wikipédia ide vágó lapját, itt
|
| Előzmény: [661] szg, 2008-11-05 22:26:20 |
|
| [662] Gyöngyő | 2008-11-06 06:50:49 |
 Sziasztok!
Segitséget szeretnék kérni,hogy hogyan lehet Mapleval megoldani az alábbi feladatokat:B.3942,B3944,B.3948. Elöre is köszönöm!
Gyöngyő
|
|
| [661] szg | 2008-11-05 22:26:20 |
 Hali abban szeretném a segítségeteket kérni, hogy hogy tudom megkapni cos(x)-ből x-et? Vagy esetleg két egyenes által közbezárt szöget? Előre is köszönöm a választ vagy esetleg valami segítséget.
|
|
| [660] S.Ákos | 2008-11-05 20:56:50 |
 Sziasztok!
A következő angol mondat fordításában kérném a segítségeteket:
"Via the median-duality transforming an arbitrary triangle ABC into one formed by its medians..."
Előre is köszönöm,
Ákos
|
|
| [659] Kry | 2008-11-04 21:43:55 |
 igen középiskolás vagyok :)
a feladat cak az 1. egyenlet volt... a 2. at csak odaírtam hogy azt ne mondjátok mert odáig eljutottam
viszont közben rájöttem hogy csináljam meg ...
azért köszönöm segítettetek
|
|
| [658] rizsesz | 2008-11-04 21:05:59 |
 Középiskolás vagy :)?
A megoldás lényege egyszerűen annyi, hogy egy szám négyzete legalább 0, tehát ha kettőt összeadunk, akkor úgy lehet csak 0, ha mindkettő 0. Így jön ki a 43 és a -12. :)
A két egyenlet amúgy ekvivalens; ez azt jelenti, hogy ugyanazt mondják ki lényegében - azaz ha kifejted az alsóban a zárójeleket, akkor pont a felsőt kapod meg - tehát az egyik felesleges.
|
| Előzmény: [656] Kry, 2008-11-04 14:28:38 |
|
| [657] jonas | 2008-11-04 15:41:32 |
 A két egyenlet, amit felírtál, ekvivalens. Egy valós megoldása van, az x=43,y=-12, meg sok komplex megoldása, amiket együtt ennél egyszerűbben már nem lehet megadni.
|
| Előzmény: [656] Kry, 2008-11-04 14:28:38 |
|
| [656] Kry | 2008-11-04 14:28:38 |
 egy eggyenletben szeretnék segítségeteket kérni ... kimondottan a nevét sem tudom ennek a fajtának... és favágó módszerrel elég ronda számok jönnek ki
egy megoldóképletet vagy akár csak a nevét előre is köszönöm
|
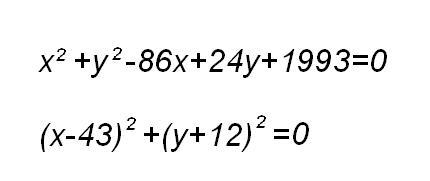 |
|
|
| [654] sakkmath | 2008-10-31 17:17:06 |
 A [602]-es és [631]-es hozzászólásokban látott feladat beküldési határideje a Monthly-ban lejárt. A feladatot sikerült megoldanom, s most közlöm e megoldást két, (remélhetően) egymást követő hozzászólásomban. Íme az I. rész:
|
 |
| Előzmény: [631] sakkmath, 2008-10-07 11:40:12 |
|