|
| [780] MTM | 2009-02-12 19:16:49 |
 Csak úgy...:]
A feladat: C. 593. Péter a bélyeggyűjteményéből az 1,2,3,...,37 forintos bélyegek mindegyikéből kivett egy-egy darabot. Szeretné ezeket úgy csoportosítani, hogy mindegyik csoportban ugyanannyi legyen a bélyegek névértékének összege. Hányféleképpen teheti ezt meg?
Minta a dolgozatok fejlécéhez C. 593. Nagy 163 Róbert 9. évf. Győr, Révai M. Gimn. e-mail: robi@revai.hu
Jelöljük a kapitány életkorát (években kifejezve) K-val, a hajóét H-val. A hajó H-K évvel ezelőtt volt annyi idős, mint a kapitány most; akkor a kapitány K-(H-K)=2K-H éves volt. Amikor a hajó 2K-H éves lesz, akkor a kapitány ...
|
| Előzmény: [779] rizsesz, 2009-02-12 19:02:06 |
|
|
| [778] vihand | 2009-02-12 18:53:17 |
 Helló, valaki meg tudja nekem röviden írni, hogy hogy kell kinéznie egy kísérőjegyzéknek? Sajnos elhagytam az első újságot, és eddig abból néztem ki. Nem sürgős, de örülnék neki. Előre is köszönöm a segítséget.
|
|
| [777] sakkmath | 2009-02-12 13:31:34 |
 Vázlatosan:
1) Az első egyenlet értelmezése.
2) Egy adott helyettesítéssel felírhatjuk a konvex függvényekre vonatkozó Jensen-egyenlőtlenséget.
3) A számtani - mértani közép összefüggésének kétszeri alkalmazása.
4) Az első pontban kapott eredménnyel kijön a megoldás.
|
| Előzmény: [776] komalboy, 2009-02-12 10:57:31 |
|
| [776] komalboy | 2009-02-12 10:57:31 |
 Sziasztok! a követekző feladatra keresek megoldást...
|
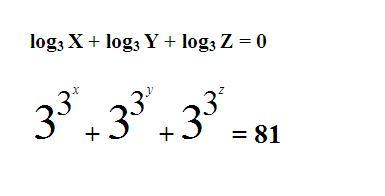 |
|
|
|
|
| [772] Bocsa Dávid | 2009-02-03 16:48:07 |
 Nagyon szép megoldás:D Köszönöm szépen. Ha esetleg tud vki másik megoldást, akkor ossza meg velem, mert tudomásom szerint több módon is bizonyítható, de egészen eddig egyre sem jöttem rá. Még egyszer köszönöm.
|
|
| [771] HoA | 2009-02-03 12:55:41 |
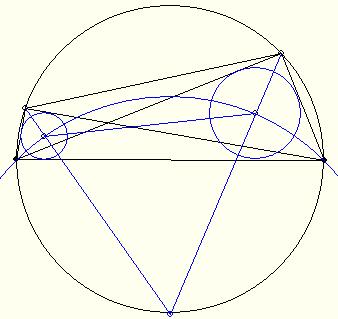
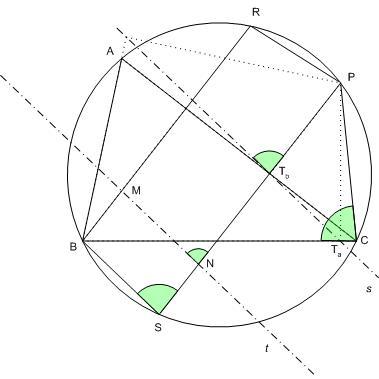
 Legyen az ABC  körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC  magasságpontja. t definíciója miatt t minden Q pontjára igaz, hogy a QP felezőpontja s-en van, így természetesen M-re is. magasságpontja. t definíciója miatt t minden Q pontjára igaz, hogy a QP felezőpontja s-en van, így természetesen M-re is.
|
 |
| Előzmény: [770] Bocsa Dávid, 2009-02-02 21:38:36 |
|
| [770] Bocsa Dávid | 2009-02-02 21:38:36 |
 Bizonyítsuk be, hogy a Simson-egyenes felezi az MP szakaszt, ahol M a háromszög magasságpontja és P a Simson egyenes P pontja a háromszög körülírt körének körívén. Vki ötlet?
|
|
| [769] jenei.attila | 2009-02-02 21:32:36 |
 Ha az adott pont 2 egységnél közelebb van a tengelyhez, akkor könnyű dolgod van. Egyszerűen ráilleszted a körlap szélét a tükrözendő P pontra úgy, hogy a körvonal két pontban metssze a tengelyt. Megjelölöd ezt a két pontot, majd a körlap szélét úgy illeszted ezekre, hogy most az előző helyzethez képest a tengelyre szimmetrikusan helyezkedjen el a körlap, majd körberajzolod a körlapot (a tengelyen kijelölt egymáshoz két egységnél közelebbi pontokra kétféleképpen-tengelyszimmetrikusan-illeszthető a körvonal). Ugyanezt megcsinálod mégegyszer úgy, hogy most az körvonal másik két pontban metssze a tengelyt. A körlap körberajzolásával adódó két körvonal metszéspontja a tengely másik oldalán megadja P tükörképét. Ha 2 egységnél távolabb van P a tengelytől, akkor segéd tengelyeket vehetsz fel úgy, hogy azok az eredeti tengely egy pontján menjenek át. A segédtengelyeket a fent leírt módon tükrözheted az eredeti tengelyre. Így az eredeti tengellyel együtt páratlan sok egy ponton átmenő tengelyed lesz, amelyekre sorban elvégezve a tükrözéseket (először a P-hez legközelebbi tengelyre türözve, majd továbbtükrözve a következő tengelyre, stb.) páratlan sok tükrözés után megkapod P tükörképét.
|
| Előzmény: [768] Ágoston, 2009-02-02 20:22:25 |
|
| [768] Ágoston | 2009-02-02 20:22:25 |
 Adott a síkon egy pont és egy egyenes. Körző használata nélkül szerkesszük meg a pontnak az egyenesre vonatkozó tükörképét. Használhatunk egyenes vonalzót a szokásos módon és egy egységsugarú körlapot, aminek nem ismerjük a középpontját. Ez utóbbit körvonalzóként használhatjuk, vagyis a síkon adott ponton, illetve pontokon átmenő egységsugarú körvonalakat tudunk rajzolni, de a középpontokat nem tudjuk bejelölni.
Valaki tudja a fenti feladatra a megoldást? Köszönöm
|
|
| [767] Tibixe | 2009-01-31 11:06:04 |
 Közben leesett, hogy amit tegnap írtam, az elég nagy hülyeség... Bocsássatok meg, elég álmos lehettem.
|
|
| [766] Tibixe | 2009-01-30 23:19:16 |
 Amit nekem sikerült, röviden:
Egy d=q-p behelyettesítés, utána a (p+d)p binomiális tételes kibontása, utána az egész szerencsétlenség leosztása pp+d-vel. Amit kapunk, az éppen a
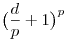
kibontott alakja lesz. Na ennek kéne 1-gyel egyenlőnek lennie. Tehát
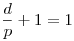
( esetleg -1, de az gyorsan kizárható ), innen pedig
d=0
.
|
|
|
| [764] Tibixe | 2009-01-30 20:14:52 |
 Úgy látszik eltér a humorérzékünk.
|
|
| [763] nadorp | 2009-01-30 19:24:28 |
 Köszi az építő megjegyzést, azért nem kell mindjárt leszedni az emberről a keresztvizet egy egyébként jó és nem bonyolult megoldás miatt ( lásd hentes) :-( Egyébként a számelmélet tele van analízist is tartalmazó bizonyítással,ezért nem értek Veled egyet teljesen. Én a pozitív egészeknek azt a tulajdonságát használtam, hogy számtani sorozatot alkotnak, Te meg a számelmélet alaptételét. Mindkettő jó. Ennyi.
|
| Előzmény: [761] Tibixe, 2009-01-30 16:26:18 |
|
| [762] Tibixe | 2009-01-30 16:36:04 |
 Hoppá,
sut tus tus
helyett
sut tus tus
-et akartam írni.
|
|
| [761] Tibixe | 2009-01-30 16:26:18 |
 Az analízissel szenvedjenek csak a fizikusok, az esetszétbontogatással meg a hentesek... Gyönyörűen kijön számelmélettel.
Vegyük mindkét oldal p alapú logaritmusát.
qp=(logp q) pq
Tehát logpq racionális, t/s alakban felírható, ahol t és s relatív prím egészek.
Innen
sqp=tpq
Ekkor lesz egy u pozitív egész szám, amire
p=ut q=us
Visszahelyettesítve:
t usut=s utus
Az általánosság megszorítása nélkül feltehetjük, hogy
sut ts ts
. Az előző egyenlet mindkét oldalát osztva:
t=s utus-sut
Az előző feltétel miatt utus-sut egész. Mivel t és s pozitív relatív prím egészek, utus-sut csak 1 lehet. Tehát t=s. Az egyetlen önmagával rel. prím pozitív egész pedig az 1. Innen pedig
p=u1=q
|
|
| [760] nadorp | 2009-01-30 08:09:03 |
 Ha p=1 akkor q=1 és fordítva, tehát ezekben az esetekben igaz az állítás. Feltehető, hogy p,q 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz 2. Tegyük fel, hogy p<q. Ekkor a feladatban szereplő egyenlőség úgy állhat fenn, ha p kitevője nagyobb, azaz
qp>pq
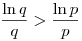
Mivel az 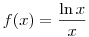 függvény x függvény x e esetén szigorúan monoton csökken, ezért 3 e esetén szigorúan monoton csökken, ezért 3 p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor p<q esetén a fenti egyenlőtlenség nem állhat fenn. Marad a p=2 eset. Ekkor
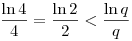 miatt szintén a monoton csökkenésből adódóan q<4,tehát csak q=3 lehet. Viszont a p=2 q=3 értékek esetén nem teljesül az eredeti egyenlőség. Azt kaptuk, p<q nem lehet. Teljesen hasonlóan adódik, hogy p>q sem lehetséges, tehát p=q miatt szintén a monoton csökkenésből adódóan q<4,tehát csak q=3 lehet. Viszont a p=2 q=3 értékek esetén nem teljesül az eredeti egyenlőség. Azt kaptuk, p<q nem lehet. Teljesen hasonlóan adódik, hogy p>q sem lehetséges, tehát p=q
|
| Előzmény: [759] Kiss Béla, 2009-01-29 20:53:36 |
|
| [759] Kiss Béla | 2009-01-29 20:53:36 |
 Sziasztok! Sagítséget szeretnék kérni a következő feladathoz. Foggalmam sincs, hogy hogyan lehetne megoldani:
Bizonyítsuk be, hogyha a p és q pozitív egész számokra fenn áll a pqp=qpq, akkor p=q.
|
|
|
| [756] Gyöngyő | 2009-01-24 10:26:40 |
 Sziasztok!
Lenne egy kérdésem!
Tudjuk,hogy 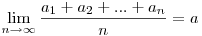
bizonyítsuk be,hogy
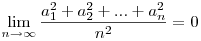
ahol ai pozitív valós számok.
Üdv.: Gyöngyő
|
|






 körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC
körülírt körének P pontjából az a oldalra bocsátott merőleges talppontja Ta, a b oldalra bocsátott merőleges talppontja Tb, a körrel alkotott második metszéspontja S. A B-ből induló magasság és a körülírt kör második metszéspontja R. Az s Simson egyenes P-ből vett kéteszeres nagyítása a t egyenes, ennek metszéspontjai BR-rel M, PS-sel N. PCTaTb húrnégyszög, mert Ta és Tb PC Thálesz-körén vannak. PC Ta = PCB szög egyenlő a Tb -nél lévő külső szöggel. PCB és PSB szögek is egyenlők, mint a PB húrhoz tartozó kerületi szögek. Végül s és t egyenesek párhuzamossága miatt PNM szög is az előbbiekkel egyenlő. PRBS szimmetrikus trapéz, mint a körből két párhuzamos húr által kimetszett négyszög. Az N-nél ill. S-nél lévő szögek egyenlősége miatt NPRM is szimmetrikus trapéz. t definíciója miatt PTb=TbN, a PN-re merőleges AC tehát NPRM szimmetriatengelye, így R és M egymás tükörképei AC-re. Mivel a magasságpont oldalegyenesre vett tükörképe a körülírt körön van, M az ABC 


 tus
tus tus
tus