| [845] pvong17 | 2009-03-02 00:00:39 |
 Én kérek bocsánatot. Nem irtam le pontosan a feladatot és megzavart egy másik feladat. (Konkrétan Obádivics Gy. Lináris algebra -zöld könyv- 258.o 3.példája, ami ezek szerint hibás , mert egy nem szimm mátrixról(valós) állitja hogy poz defeinit, majd utána be is bizonyitja ezt :) )
Most már nincs probléma, mert sikerült letisztáznom a dolgokat. Köszönöm a gyors reakciót.
|
| Előzmény: [844] Lóczi Lajos, 2009-03-01 20:46:41 |
|
|
|
|
| [841] pvong17 | 2009-03-01 15:21:48 |
 Ha egy nem szimmetrikus mátrixnak, létezik negatív sajátértéke akkor már nem is lehet pozitív definit, ugye ?
(bocsánat ha triviális)
|
|
| [840] fityfiritty | 2009-02-26 17:01:02 |
 Nagyon jó!! Köszönöm Neked is és Jonasnak is a profi, klassz válaszokat, tanácsokat. Most már meg merem kockáztatni, hogy az ex hatványsorának az x = -1- hez tartozó részletösszegéhez jutottunk, ha nem tévedek. Ezért a limeszre a tippem: 1/e. Üdvözöl mindenkit: fityfiritty.
|
| Előzmény: [832] nadorp, 2009-02-25 15:50:24 |
|
| [839] sakkmath | 2009-02-26 12:20:11 |
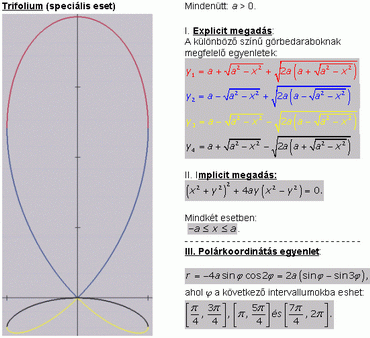
 Az egyes levelek területeire én is ezeket az eredményeket kaptam. Levezetésedben a teljes területre, mint adott értékre támaszkodsz. Hogy ez a szál se legyen elvarratlan, felteszem az alábbi ábrát, amely további adatokat szolgáltat a görbéről. Így bárki összevetheti saját eredményeit az általam közöltekkel... .
|
 |
| Előzmény: [833] HoA, 2009-02-25 16:40:55 |
|
|
|
|
|
|
| [833] HoA | 2009-02-25 16:40:55 |
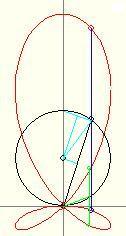
 Ha a választott abszcisszához tartozó két másik metszéspontot is bejelöljük ( zöld szakasz végpontjai ) és a görbe által határolt területet integrálszámítással, a görbe alatti területek különbségeként számítjuk, az x tengely alatti értékeket szokás szerint negatívnak véve, akkor eredményül a nagy levél területének és a két kis levél területének különbségét kapjuk. Ha OC az y tengellyel  szöget zár be, a kis kék háromszögekből az infinitezimális területdarab szöget zár be, a kis kék háromszögekből az infinitezimális területdarab  Td=4a(cos Td=4a(cos -sin -sin )2acos2 )2acos2   , amiből a teljes terület , amiből a teljes terület
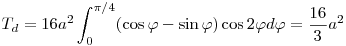
Érdekes, hogy ez a terület a2-nek racionális számszorosa. Elfogadva, hogy a területek abszolút értékének összege
Ts=2 a2 a2
, a felső levél területét T1-gyel, a két kis levél területének összegét T2 -vel jelölve
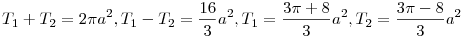
A számértékeket behelyettesítve azt kapjuk, hogy T1 nagyjából 92,5 , T1 pedig 7,5 százaléka a teljes területnek. ( ha jól számoltam ... :-) )
|
 |
| Előzmény: [804] sakkmath, 2009-02-17 13:20:30 |
|
|
| [831] jonas | 2009-02-25 13:45:05 |
 Az ilyen fajta feladatra van egy általános módszer, ami gyakran működik. Számold ki a rekurziós szabályból a sorozat első néhány elemét pontosan. Keress rá a számlálójukra az OEIS-ben, megtalálod az A053557 sorozatot egyetlen találatként. Ennek a leírása azt mondja, hogy a sorozat n-ik eleme a 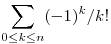 szám számlálója, ebből megsejted, hogy a te an sorozatod általános tagja éppen ez az összeg lesz, de vigyázz, az index eggyel el van csúsztatva! Ellenőrzöd, hogy ez a sejtés igaz-e az első néhány tagra, aztán ha igen, akkor megpróbálod belátni teljes indukcióval, hogy ez az explicit képlet valóban mindig igaz. Ezután már csak be kell látnod, hogy ez hova konvergál. szám számlálója, ebből megsejted, hogy a te an sorozatod általános tagja éppen ez az összeg lesz, de vigyázz, az index eggyel el van csúsztatva! Ellenőrzöd, hogy ez a sejtés igaz-e az első néhány tagra, aztán ha igen, akkor megpróbálod belátni teljes indukcióval, hogy ez az explicit képlet valóban mindig igaz. Ezután már csak be kell látnod, hogy ez hova konvergál.
|
| Előzmény: [830] fityfiritty, 2009-02-25 12:48:20 |
|
| [830] fityfiritty | 2009-02-25 12:48:20 |
 Sziasztok, remek ez a Fórum, le a kalappal! A sok érdekes, okos hozzászólás felbátorított, hogy tőletek kérjek segítséget ehhez a feladathoz: Az (an) sorozat elemeit így definiáljuk:
a0 = 1; a1 = 0; 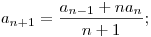 ha n = 1, 2, .... . Konvergens-e az (an) sorozat? Ha igen, akkor mi a határértéke? ha n = 1, 2, .... . Konvergens-e az (an) sorozat? Ha igen, akkor mi a határértéke?
Köszi szépen, előre is!
|
|
| [829] laci777 | 2009-02-24 16:15:51 |
 Én köszönöm, mégpedig Neked, valamint Káli Gúlának a hasznos útmutatást. Túl azon, hogy egy magamban már eléggé reménytelennek elkönyvelt problémában segítettetek, élvezet volt számomra a gondolatmeneteteket is követni.
A gordiusi csomó átvágását - tekintettel a valóban csúnya paraméteres megoldásra - külön is köszönöm:)
Szép napot: Laci
|
| Előzmény: [827] HoA, 2009-02-24 14:08:59 |
|
|
| [827] HoA | 2009-02-24 14:08:59 |
 Köszönöm Káli gúla szép megoldását. Azt hiszem, segít még jobban rávilágítani arra, mi a bajom ezzel a feladattal. Fussunk tehát neki harmadszor is, ezúttal az ő jelöléseit is használva:
Egy egyenletes v1 sebességgel haladó, M méter hosszú menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott t mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont M métert tesz meg. A kérdés, mekkora utat tett meg a futár összesen? ( Számadatok: t = 15 s , M = 1000 m )
A futár megtett útja [822] megoldóképlete szerint így alakul:
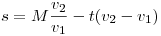 | (1) |
Mint az várható volt, a megtett út a feladatban szereplő M,t,v1ésv2 mennyiségektől függ. M és t konkrét értéke adott, de v1ésv2 szerepét jótékony homály fedi. Gondolhatnánk, hogy azok is az M és t ismeretében értelmes határok között szabadon megadhatók, csak most éppen nem rendelünk hozzájuk számértéket. De ez nem így van. A feladat túlhatározott, adott M és t mellett már v1ésv2 nem választható meg egymástól függetlenül. Az adatok közötti megkötést éppen [822] feltételi egyenlete adja:
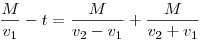 | (2) |
Ha M,v1ésv2 értéke lenne adott, megtehetnénk, hogy (2) –ből kifejezzük t-t és ezt behelyettesítjük (1) –be. Rövid átalakítások után [824] szép képletét kapjuk:
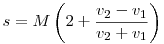 | (3) |
De az ekkor sem lenne igaz, hogy „akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát”, hiszen egy adott M,v1ésv2 hármashoz egy konkrét, éppen a (2) egyenletből adódó t érték tartozik.
Nekünk azonban Mést adott. Mit tehetünk, hogy bemenő adatainktől egyértelműen függő eredményt kapjunk? Az egyik megoldás laci777 „izzadási iránya”: (2) –ből v2-re másodfokú egyenletet kapunk. Ennek fizikailag értelmes gyökét választva v2 -nek ezt a kifejezését behelyettesítjük (1) –be és kapunk egy csúnya , de csak M-et,t-tésv1-et tartalmazó kifejezést. A másik megoldás az, hogy elfogadjuk (3) szép képletét megoldásnak, de hozzátesszük, hogy „ahol v1 szabadon választott sebesség a 0<v1<M/t tartományban, v2 pedig a (2) feltételből számított M,t,ésv1 által meghatározott sebesség”. És ekkor persze a (3) képletben szereplő mennyiségekhez éppen a megadott t érték trtozik.
|
| Előzmény: [824] Káli gúla, 2009-02-23 19:14:32 |
|
| [826] tudniakarok | 2009-02-24 13:46:11 |
 Sziasztok! Kérlek segítsetek!
Az a problémám, hogyha adott tetszőleges db nemnegatív szám, akkor hogyan tudnám elrendezni őket egy mátrixba úgy hogy a lehető legegyenletesebb elrendezést kapjam.(Arra gondolván, hogy a két legnagyobb szám a "legtávolabb" legyen egymástól, és így tovább...) Van-e erre vmilyen már kidolgozott algoritmus, mert nem nagyon találom a szakirodalmakban!? Van ötletem, de elég egyszerűnek találom ráadásul nagy számításigényű,hátha vki tud jobbat!
Előre is köszi a segítséget!
|
|
| [825] laci777 | 2009-02-23 23:22:06 |
 Kedves Káli Gúla!
Köszönöm szépen ezt a megoldást is, bár őszintén szólva olyat igyekeztem volna kiizzadni (a jelzett eredménnyel:(), ahol a menetoszlop (a példa adatai szerint 0<v1<240 km/h közt értelmezhető) sebessége az egyedüli független változó, ahogyan valóban is annak a függvénye minden egyéb tényező (a v2 és az egyes szakaszok s és t értékei egyaránt). Még egyszer köszönöm.
|
| Előzmény: [824] Káli gúla, 2009-02-23 19:14:32 |
|
| [824] Káli gúla | 2009-02-23 19:14:32 |
 Működik az is. Legyen v2=kv1, a menetoszlop hossza M. Amíg fel- és lefut, addig 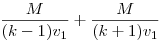 idő telik el, ez alatt a menet idő telik el, ez alatt a menet 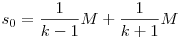 , a futár pedig , a futár pedig 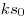 utat tesz meg. A középső időszakban együtt mennek, ez a feltétel miatt utat tesz meg. A középső időszakban együtt mennek, ez a feltétel miatt 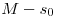 , tehát a futár összesen , tehát a futár összesen 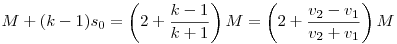 utat tett meg a feladat adataival (akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát vagy ha 0 mp-et ment volna). utat tett meg a feladat adataival (akkor is, ha 15 mp-ig megy elöl, és akkor is, ha 100 órát vagy ha 0 mp-et ment volna).
|
| Előzmény: [823] laci777, 2009-02-23 16:53:01 |
|
| [823] laci777 | 2009-02-23 16:53:01 |
 Kedves HoA!
Köszönet (ismét) a segítségért. Úgy gondoltam eredetileg, hogy az egyes időintervallumokban megtett utakkal operálok, de boncolás (+eltévedés:() lett sajna belőle...
Még egyszer köszönöm szépen.
|
| Előzmény: [822] HoA, 2009-02-23 10:08:45 |
|
| [822] HoA | 2009-02-23 10:08:45 |
 Szerintem a feladatban nem az okozza a gondot, hogy „a megoldáshoz vezető másodfokú egyenlet túl kemény dió” , hanem az, hogy a feladat egy kicsit tisztességtelenül van kitűzve. Az egyik szokásos középiskolai feladattípus szövegében megadnak bizonyos paramétereket és az eredményt ezek függvényében várják. Ha zárójelben megadják a paraméterek numerikus értékét is, akkor ezeket az eredmény képletébe behelyettesítve számszerű eredményt is tudunk adni . Másik fekadattípus az, ahol egy fizikai jelenség kapcsán bizonyos mennyiségek közötti összefüggések keresése, értékhatárok megállapítása a cél. Itt a kettő keveredik, a baj csak az, hogy ez a szövegből nem derül ki egyértelműen. Tisztességesnek valahogy így érezném a feladat kitűzését:
Egy egyenletes v1 sebességgel haladó menetoszlop végéről t0 időpontban egy futár szintén egyenletes v2 sebességgel az oszlop legelejére megy. Ott 15 mp-ig az oszloppal halad, majd az eredeti v2 sebességével az oszlop végére visszamegy. Mire visszaér, a folyamatosan haladó menetoszlop t0 időponttól pont 1 km-t tesz meg. A kérdés, mekkora utat tett meg a futár összesen? Milyen összefüggés áll fenn v1 és v2 között, ha tudjuk, hogy a menetoszlop 1 km hosszú?
Megoldás: A futár teljes menetideje 1000/v1 mp, ebből 15 mp-ig v1, egyébként v2 sebességgel haladt, a megtett út tehát s =  méter. A v1ésv2 közötti összefüggést abból állapítjuk meg, hogy a futár 1000/v1-15 mp alatt az 1000 méteres oszlop végéről az elejére majd vissza ment, menetideje tehát: méter. A v1ésv2 közötti összefüggést abból állapítjuk meg, hogy a futár 1000/v1-15 mp alatt az 1000 méteres oszlop végéről az elejére majd vissza ment, menetideje tehát: 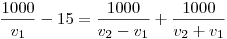 Ezek után a v2-re adódó másodfokú egyenletet elemezhetjük, milyen v1 értékekre kapunk pozitív v2-t, v2 milyen határok között változhat, stb. Végül v2-t v1 függvényeként felírva behelyettesíthetjük a megtett út képletébe, így az egy csak v1 -től függő kifejezés lesz, de továbbra sem egy konkrét számérték. Ezek után a v2-re adódó másodfokú egyenletet elemezhetjük, milyen v1 értékekre kapunk pozitív v2-t, v2 milyen határok között változhat, stb. Végül v2-t v1 függvényeként felírva behelyettesíthetjük a megtett út képletébe, így az egy csak v1 -től függő kifejezés lesz, de továbbra sem egy konkrét számérték.
|
| Előzmény: [815] laci777, 2009-02-22 00:21:36 |
|
| [821] Lóczi Lajos | 2009-02-22 18:20:58 |
 Rögzített x H-ra n H-ra n  esetén fn(x) esetén fn(x) f(x):= f(x):= x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy x/2. A függvénysorozat egyenletes konvergenciája azt jelenti, hogy  . Ezt kell igazolni most. Ehhez egy kis függvényvizsgálatra van szükség. . Ezt kell igazolni most. Ehhez egy kis függvényvizsgálatra van szükség.
1. Látszik, hogy ha x rögzített, akkor a konvergencia n-ben monoton: fn(x)<fn+1(x)<f(x), vagyis |fn(x)-f(x)|=f(x)-fn(x)=:gn(x).
2. Pl. L'Hospital-lal belátod, hogy  illetve két deriválással, hogy gn(x) konkáv. De gn(0)=0 is igaz. Vagyis rögzített n-re gn olyan nemnegatív konkáv függvény, amely 0-ban 0, a végtelenben pedig a határértéke pozitív. Egy ilyen függvény viszont minden x illetve két deriválással, hogy gn(x) konkáv. De gn(0)=0 is igaz. Vagyis rögzített n-re gn olyan nemnegatív konkáv függvény, amely 0-ban 0, a végtelenben pedig a határértéke pozitív. Egy ilyen függvény viszont minden x H esetén kisebb, mint a limesze, tehát H esetén kisebb, mint a limesze, tehát 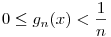 , minden x-re és n-re. , minden x-re és n-re.
3. Emiatt 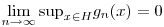 . .
|
| Előzmény: [819] plac, 2009-02-22 14:22:15 |
|








 (0,1),
(0,1),  (X)<+
(X)<+ esetén), hogy a végeredmények rendre +
esetén), hogy a végeredmények rendre +
 szöget zár be, a kis kék háromszögekből az infinitezimális területdarab
szöget zár be, a kis kék háromszögekből az infinitezimális területdarab  Td=4a(cos
Td=4a(cos a2
a2


