Fórum: Valaki mondja meg!

Milyen módszerrel javasoljátok az 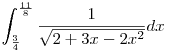integrál kiszámolását? Illetve milyen helyettesítés a legelőnyösebb?

Az n=4-re végtelen leszállással lehet bizonyitani pl., ami eleminek mondható.

Most már otthon vagyok és megnéztem a Szalay: Számelmélet könyvet. Az n=4 esetre leír egy nem túl nehéz elemi megoldást. Az n=3 esetet nem bizonyítja, de megemlíti, hogy az Euler-egészek segítségével látták be.

és n=3-ra van elemi bizonyítása...rossz napom van

n=3 van az Euler egészekkel. bocsánat

Freud: Számelmélet könyvében benne van az n=4 és az n=3 eset is, de az n=4 Euler-egészekkel (ha jól emlékszem). Gábor azt állította, h az előbbire van középiskolás módszerekkel megoldása. Én szkeptikus vagyok, de ne legyen igazam:) Szerintem egyszer mindenki megkísérli bizonyítani az n=3,4-et aki olvasott gimiben Fermat sejtésről...(aztán az esetek többségében besül a próbálkozás)

Most nem otthon vagyok, úgyhogy nem tudom ellenőrizni, de a Szalay: Számelmélet könyvben nincs benne az n=3 és az n=4 esetek bizonyítása?

Szerintem nincs kizárva, hogy bizonyitható, n=4 esetre pl. elég "könnyű" a bizonyitás, én is kiváncsian várom a bizonyitásodat.

Könnyen meglehet. Írd be, szívesen átrágjuk rajta magunkat.

Üdv! Csak azt szeretném kérdezni hogy szerintetek gimis matekkal bizonyítható-e a Fermat sejtés n=3 esete?Szerintem sikerült csak még nem írtam le!:D:D:D

Továbbra is úgy értelmezem a kérdést, hogy "Hány olyan elem van 64 elemű testben, amely nincs benne valódi résztestben?" Ennek a testnek valóban csak 2,4 és 8 elemű résztestei lehetnek mivel minden test vektortér bármelyik részteste felett, ahogy Fálesz Mihály is írta. Ilyen résztestei pedig valóban vannak is, mégpedig mindegyikből csak 1-1. Ez a test (GF(64)) a x⁶⁴-x polinomnak felbontási teste (e testben lineáris gyöktényezők szorzatára bomlik), sőt pontosan a x⁶⁴-x polinom gyökei alkotják a test elemeit. Az, hogy ennek a testnek van 2, 4 és 8 elemű részteste abból következik, hogy a x²-x, x⁴-x és x⁸-x polinomok osztói a x⁶⁴-x polinomnak, amelyek gyökei így szintén GF(64) elemei. Ezek a gyökök könnyen bizonyíthatóan résztesteket alkotnak, mert (x+y)²=x+y,(xy)²=xy,(-x)²=-x,(x^-1)²=x^-1 (itt kihasználtuk, hogy a test 2 karakterisztikájú). Hasonlóan 4 és 8 kitevővel. Más 2, 4 és 8 elemű résztestei GF(64)-nek nincsenek, mint a most felsorolt polinomok gyökeiből álló testek, mert az azt jelentené hogy a x²-x, x⁴-x és x⁸-x polinomoknak 2,4 illetve 8-nál több gyökük lenne ami lehetetlen. A 2 elemű (0,1 -et tartalmazó) résztest részteste a 4 és 8 elemű testeknek is, azonban a 4 elemű résztest nem részteste a 8 eleműnek (mivel a 8 elemű test nem lehet vektortér a 4 elemű felett). Vagyis e résztestek uniója 10 elemet tartalmaz, a maradék 54 elem pedig egyik résztestnek sem eleme.

A Wikipedia szerint ez egy ismert probléma, amelyre eddig nem találtak polinom futásidejű algoritmust, és azt sem tudják, hogy van-e; viszont az inverzét, a hatványozást könnyű hatékonyan elvégezni. Ha jól tudom, az sem ismert, hogy léteznek-e bizonyítottan ilyen tulajdonságú ún. csapóajtófüggvények.

The existence of one-way functions

Nézzük. A 7-1 prímfelbontása 2^.3, úgyhogy elég a második és harmadik hatványt megnézni, ha egyik sem 1, akkor a rend 6. Mármost 3²=92mod 7 az nem 1, és 3³2*3=6 szintén nem 1, tehát a 3 rendje 6.

Köszönöm a válaszokat. Én is így számoltam eddig, csakhát reméltem van valami hatékonyabb megoldás is... n=7-re a 3 rendjéért már meg kell szenvedni (szg. nélkül).

Végignézheted szép sorban b^d-t minden szóba jöhető d-re, azaz amikor d poz. egész és osztja (n)-t, aztán ha 1 maradékot ad, akkor az aktuális d lesz a válasz. Kis n-re ez is jó.

Üdv. Freud: Számelmélet című könyvében pl. utána lehet nézni, de a google is segíthet:) a rend emlékeim szerint a legkisebb ,,jó'' kitevő és osztója minden jó kitevőnek pl. fi(n)-nek is. fi(n) n-ig az n hez relatív prímek száma. Konkrét b és n esetén tehát a rend a fi(n) osztói közül kerül ki. Régen tanultam ezekről talán diszkrét logaritmus(index) címszóval keresd a problémát.

Sziasztok!

Egy kis segítségre lenne szükségem: Rn redukált maradékosztályok csoportjában hogy kell elem rendjét kiszámolni? Vagy ami ezzel ekvivalens, b a k-adikon kongruens 1 modulo n egyenletet hogy kell megoldani? (b és n ismert)

Üdv: Borel

Igaz. Ezen még gondolkozok.

Köszönöm szépen!

A 64-elemű testnek csak 2-, 4- és 8-elemű résztestei vannak.

A bővebb test vektortér a résztest felett, ezért az elemszáma csak hatványa lehet a résztest elemszámának.

"Hány olyan elem van 64 elemű test felett...", ezt úgy érted, hogy "Hány olyan elem van 64 elemű testben..."? Ha igen, akkor szerintem 32. Mivel a 64 elemű test legbővebb valódi részteste 32 elemű és a többi résztest ennek részteste, a maradék 32 elem nem eleme egyetlen résztestnek sem.

Valki segítene ebben a feladatban? Hány olyan elem van 64 elemű test felett amely nincs benne valódi résztestben?

Elöre is köszönöm!

Biztos van egyszerűbb megoldás is ( maradékosztályokat felhasználó vagy gráfelméleti), de ezt nem találtam.

Jelölje A_i azon függvények halmazát,melyek maximuma i. Ekkor ha 0ik ,akkor

A_i elemszáma (k+1)ⁿ-kⁿ,mert

fA_i esetén i-kf(j)i, tehát f k+1 féle értéket vehet fel, így azokat a k+1 elemből képezhető n hosszú sorozatokat kell leszámolni, melyek legalább egyszer tartalmazzák az i-t.

Ha pedig -ki-1, akkor a fentihez hasonlóan

A_i elemszáma (i+k+1)ⁿ-(i+k)ⁿ

A fenti módszerrel minden függvényt pontosan egyszer számoltuk, hiszen egy A_i-n belül a függvények különböznek és ij esetén minden A_i-ben szereplő függvény eltér minden A_j-ben szereplő függvénytől, mert a maximumuk különböző. Az összes függvény száma

(1ⁿ-0ⁿ)+(2ⁿ-1ⁿ)+...+(kⁿ-(k-1)ⁿ)+(k+1)((k+1)ⁿ-kⁿ)=(k+1)ⁿ⁺¹-kⁿ⁺¹

Nagyrabecsült FÓRUMOSOK! Sehogy sem bírok ezzel a feladattalÿ:( segítenétek?

Legyenek n és k adott pozitív egészek és tekintsük azon f: {1; 2; 3; ...; n} {-k; -k+1; ...; k-1; k} függvényeket, amelyekre |f(i) - f(j)|k bármely i, j {1; 2; 3; ...; n} esetén. Hány ilyen f függvény van?

Üdv: gubanc

Talán ez is segít (a részleteket a könyv mellőzi):