| [930] Sirpi | 2009-04-15 10:01:48 |
 Ha már nagy számoknál tartunk, leírok két módszert nagyon nagy számok (precízebben: hihetetlen gyorsan növő sorozatok) előállítására. Az elsőnek a nevét is tudom, ezek a jól ismert Ackermann-számok:
Vegyünk egy kétváltozós "sorozatot", tehát A(m,n)-et (m,n 1), és legyen A(m,1)=2m (tehát rácsba rendezve az első sor a 2,4,6... sorozat), valamint legyen A(1,n)=2 (tehát az első oszlop csupa 2-es). Ezek után egy még nem ismert A(m,n) elemet úgy számolunk ki, hogy megnézzük, hogy tőle balra mi áll (vagyis A(m-1,n)-et), és a fölötte lévő sor annyiadik elemét írjuk be az (m,n) helyre. Formálisan: 1), és legyen A(m,1)=2m (tehát rácsba rendezve az első sor a 2,4,6... sorozat), valamint legyen A(1,n)=2 (tehát az első oszlop csupa 2-es). Ezek után egy még nem ismert A(m,n) elemet úgy számolunk ki, hogy megnézzük, hogy tőle balra mi áll (vagyis A(m-1,n)-et), és a fölötte lévő sor annyiadik elemét írjuk be az (m,n) helyre. Formálisan:
A(m,n)=A(A(m-1,n),n-1)
Ezek alapján a második sor: 2, 4, 8, 16, 32 (tehát a 2-hatványok)
A 3. sor: 2 4 16 65536 265536 2265536..., a többi sor meg még gyorsabban nő. Nézzétek meg, elég hamar belebotlotok abba, hogy az elemeket már fel se tudjátok írni, mert nincs rá jelölésünk.
Azt mondjuk továbbá, hogy ha van egy sorozatunk, amit ennek a táblázatnak valamelyik (mondjuk k.) sora majorál, akkor a sorozatunk legfeljebb k Ackermann-osztályú.
Ackermann-sorozatnak a főátlót nevezik, ennek nyilván végtelen az Ackermann-osztálya.
* * *
Másik, hasonló konstrukció, ez nem tudom, kinek a nevéhez fűződik:
A számokat úgy jelöljük, hogy veszünk egy számot, és aköré szabályos sokszögeket rajzolunk (koncentrikusan, tehát a sokszögek nem metszik egymást, és van egy egyértelmű sorrendjük kifelé).
Van két kiértékelési szabályunk:
- ha az n szám egy háromszögben van, akkor a háromszöget eltüntetve nn-t írunk be helyette
- ha az n szám egy k-szögben van (k 4), akkor a k-szöget kicseréljük n db. k-1-szögre. 4), akkor a k-szöget kicseréljük n db. k-1-szögre.
Ezek után számoljátok ki, hogy mennyi a 2 egy ötszögben. Elkezdem, hátha valakinek nem világosak a szabályok, és ezáltal azok lesznek (jelölés: 2 3 3 4: a 2-es benne van egy 3-szögben és az egy négyzetben): 4: a 2-es benne van egy 3-szögben és az egy négyzetben):
2 5=2 5=2 4 4 4=2 4=2 3 3 3 3 4=4 4=4 3 3 4=256 4=256 4=... 4=...
* * *
Ezt a két konstrukciót csak azért hoztam fel, mert ebben a modellben az olyan számok, mint amiknek a nagyságrendjét az előző hsz-ekben próbáltátok elképzelni, azok is nagyon picik. Szóval ezeket már tényleg meg se próbáljátok :-)
|
|
| [929] Wesselényi-Garay Andor | 2009-04-15 00:40:35 |
 Sziasztok! Ez rengeteg segítség. Egyetlen kérdésem van már csak. Akkor ez a szám, ami a könyv univerzumának a mérete... hányszor nagyobb a mi univerzumunknál? (Lajos okfejtésében nem értettem valamit...:))
|
|
| [928] Lóczi Lajos | 2009-04-14 22:55:41 |
 De ne úgy írd, hogy "22991-szer nagyobb, mint", mert azt úgy is lehetne érteni, mintha ez a 25-hatvány 22991 db univerzumnyi atommal lenne egyenlő. Szóval, egy ekkora számot nem lehet elképzelni szerintem sehogy :)
|
| Előzmény: [927] Csimby, 2009-04-14 22:05:11 |
|
| [927] Csimby | 2009-04-14 22:05:11 |
 Pár érdekes adat:
Az univerzum mérete: 2280cm3 (legalábbis 1996-ban így saccolták, de mint tudjuk folyamatosan tágul :-)
Az univerzum kora: 259sec
Az univerzumban található atomok száma: 2265 A Föld atomjainak a száma: 2170
Forrás: Schneier, Applied Cryptography (Ha beírod gugliba, hogy "atomok száma az univerzumban", akkor az 5. link egy pdf fájl és abban a 2. oldal)
A te számod tehát  22991-szer nagyobb mint ahány atom van az univerzumban. 22991-szer nagyobb mint ahány atom van az univerzumban.
|
| Előzmény: [926] Wesselényi-Garay Andor, 2009-04-14 21:25:53 |
|
| [926] Wesselényi-Garay Andor | 2009-04-14 21:25:53 |
 Fú nagyon jó fejek vagytok, RETTENETESEN KÖSZÖNÖM és bocsánat, hogy csak most szólok, de nem látom a gépemen automatikusan frissítve az infókat.
Szóval a lehető legpontosabb - legnagyobb számra lenne szükségem - ha ez nem tőrdöfés a matematika szívébe - amit le lehet írni a lehető leghosszabban. Mivel ez egy iszonyat bődületesen nagy szám, ahogy látom itt a számításaitokból, abban is kérem a segítségeteket, hogy ezt hogyan lehet elképzelni? Meghatározni? Hogyan lehet "mérhetővé", illusztratívvá tenni ezt az iszonyat méretű absztrakciót? Teszem azt: a Föld felülete négyzetmilliméterben? Valami hasonló?
Hogy ne áruljak zsákba macskát: Borges Bábeli könyvtárának a méretére vagyok kíváncsi. Ha ezt a számot megkapjuk, akkor - nevessetek ki, de megkapjuk a magasabb rendű negyvenkettőt. A választ a "világmindenség kérdésére", arra, hogy bizonyos peremfeltételek mellett - amit Borghes ebben a gyönyörű esszéjében leír - hány könyvet lehet írni a világon. Kérlek ne nézzetek őrültnek én csak egy egyszerű képletet kaptam annak alapján, amit Borghes leír, de a számítást nem tudom elvégezni!
Andor
|
| Előzmény: [925] Csimby, 2009-04-14 20:41:27 |
|
|
|
|
| [922] jonas | 2009-04-14 20:06:37 |
 Igaz. Akkor sem giga. Tizes számrendszerben kevesebb, mint kétmillió számjegyből áll. Ezt már egy mai számítógéppel nagyon gyorsan ki lehet számolni.
|
| Előzmény: [921] R.R King, 2009-04-14 20:02:26 |
|
|
|
| [919] Lóczi Lajos | 2009-04-14 19:46:19 |
 De mire kell ez neked? Tegyük fel, itt van előtted egy fájlban a szám. Milyen tulajdonsága érdekel? A számjegyek összege? Hátulról a 26. jegy? Csak azért kérdem, mert lehet, hogy a kívánt információt a teljes alak ismerete nélkül is meg lehet kapni.
|
| Előzmény: [918] Wesselényi-Garay Andor, 2009-04-14 18:59:47 |
|
| [918] Wesselényi-Garay Andor | 2009-04-14 18:59:47 |
 Szia! Köszönöm, szerinted hol érdeklődjem tovább? Kutatóintézetek? Hol van ekkora gép? Az e-mailem: wga418@invitel.hu - esetleg ott is folytathatjuk!
|
|
|
| [916] Wesselényi-Garay Andor | 2009-04-14 15:34:05 |
 Szervusztok!
Lehet, hogy off, de egy - számomra hatalmas - kéréssel/kérdéssel szeretnék hozzátok fordulni. Tudnátok segíteni olyan program, szakértő, stb. megadásában, mely segítségével nagy számokkal lehet dolgozni? Konkrétan egy egyszerű képlet, a 25 a 1312000-en, vagyis "huszonöt az egymillióháromszáztizenkétezrediken" számot szeretném megkapni. Előre is köszönöm, tisztelettel, Wesselényi-Garay Andor
|
|
|
| [914] Cokee | 2009-04-08 20:21:10 |
 Sziasztok!
Milyen n egészre direkt felbonthatatlan Zn?
Üdv.: Cokke
|
|
| [913] zozi | 2009-04-08 14:48:03 |
 közben kiderült ,hogy rosszul adtam meg az értéktatományt így helyes (A + B) < (C / 2)
viszont ezzel az értéktartománnyal nem minden esetben oldható meg az egyenlet kérdésem az lenne , hogy meglehet e tudni hogy mely C értékeknél áll fenn az egyenlősé ,és melyeknél nem
|
| Előzmény: [912] Sirpi, 2009-04-08 12:43:00 |
|
| [912] Sirpi | 2009-04-08 12:43:00 |
 Egy 8-10 jegyű n számnál még simán megy, hogy 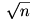 -ig (ami 4-5 jegyű) végignézed az összes számot, hogy osztható-e valamelyikkel. -ig (ami 4-5 jegyű) végignézed az összes számot, hogy osztható-e valamelyikkel.
Egyébként annyi kimaradt az előbb, hogy természetesen a negatív felbontások (pl. (-12).(-1)) is adnak megoldást a feladatra.
|
| Előzmény: [911] zozi, 2009-04-08 10:43:17 |
|
| [911] zozi | 2009-04-08 10:43:17 |
 közben rákérdeztem A is és B is < (C + 1) / 2
a megoldásod egyébként teljesen tuti
de érdekelne , hogy mit lehet tenni 2C felbontása ügyében ha C nagy szám mondjuk 8 10 digites
|
| Előzmény: [910] Sirpi, 2009-04-08 09:19:43 |
|
| [910] Sirpi | 2009-04-08 09:19:43 |
 B.(2A+B+1)=2C
2C-t bontsuk fel egy páros és egy páratlan szám szorzatára (ugyanis B és 2A+B+1 paritása eltérő), az egyik lesz a B, a másik 2A+B+1. így B ismeretében már A is meghatározható.
Példa: C=6
Ekkor 2C-t, vagyis 12-t felbontjuk egy páros és egy páratlan szám szorzatára: 12.1, 4.3, 3.4, 1.12.
Innen B=12,A=-6; B=4,A=-1; B=3,A=0; B=1,A=5
|
| Előzmény: [907] zozi, 2009-04-07 21:00:05 |
|
|
|
| [907] zozi | 2009-04-07 21:00:05 |
 sziasztok
egy ismerősöm megkérdezte , hogy megtudnám e oldani ezt
A*B + B(B + 1) / 2 - c = 0
én azt gondoltam , hogy igen de már három napja ülök rajtra és semmire sem jutottam, bár nem tünik nehéznek, és mostmár nagyon érdekelne , hogy hogyan kell megoldanu.
C -t ismerem A és B -t keresem
|
|
| [906] jonas | 2009-04-06 23:34:15 |
 Én másképpen csinálnám, de az bonyolultabb. Szedjük szét három részre az eseteket a szerint, hogy sorban az utolsó golyó milyen színű: piros, fehér, vagy kék. Jelentse p(x,y,z) a lehetséges gyönygysorok számát, amik x piros, y fehér, és z kék golyóból állnak, és ezek közül az utolsó piros; hasonlóan f(x,y,z) a lehetséges fehérre végződő sorrendek száma, és k(x,y,z) a kékre végződőek száma. Ezekre felírhatóak az alábbi rekurziós összefüggések.
p(x+1,y,z)=p(x,y,z)+k(x,y,z)
f(x,y+1,z)=f(x,y,z)+k(x,y,z)
k(x,y,z+1)=p(x,y,z)+f(x,y,z)+k(x,y,z)
Kivéve hogy a fenti egyenlőtlenségek nem igazak a p(1,0,0)=f(0,1,0)=k(0,0,1)=1 esetekre.
A peremfeltételek a következők.
p(0,y,z)=f(x,0,z)=k(x,y,0)=0
A feladatban a p(2,3,4)+f(2,3,4)+k(2,3,4) érték a kérdés. Ehhez egy táblázatba fell kell írni a p,f,k értékeit minden x,y,z értékhármasra. Ez talán kézzel is kiszámolható, ha nagyon sok türelmed van, de nekem nincs, úgyhogy számítógéppel csinálom. Ez jön ki.

Így aztán az eredmény 60+76+64=200.
Persze számítógéppel egyszerűbb, ha végigpróbálod a 9 golyó mind az 1260 sorrendjét, amiből rögtön látszik, hogy 200 jó.
|
| Előzmény: [902] Sirpi, 2009-04-06 13:17:34 |
|



 1), és legyen A(m,1)=2m (tehát rácsba rendezve az első sor a 2,4,6... sorozat), valamint legyen A(1,n)=2 (tehát az első oszlop csupa 2-es). Ezek után egy még nem ismert A(m,n) elemet úgy számolunk ki, hogy megnézzük, hogy tőle balra mi áll (vagyis A(m-1,n)-et), és a fölötte lévő sor annyiadik elemét írjuk be az (m,n) helyre. Formálisan:
1), és legyen A(m,1)=2m (tehát rácsba rendezve az első sor a 2,4,6... sorozat), valamint legyen A(1,n)=2 (tehát az első oszlop csupa 2-es). Ezek után egy még nem ismert A(m,n) elemet úgy számolunk ki, hogy megnézzük, hogy tőle balra mi áll (vagyis A(m-1,n)-et), és a fölötte lévő sor annyiadik elemét írjuk be az (m,n) helyre. Formálisan:  3
3


 22991-szer nagyobb mint ahány atom van az univerzumban.
22991-szer nagyobb mint ahány atom van az univerzumban.