|
| [966] Lóczi Lajos | 2009-07-14 15:25:01 |
 A legegyszerűbbeket alkalmas függvény Taylor-sorfejtéséből (pl. http://mathworld.wolfram.com/MaclaurinSeries.html). A többi után érdemes a szerzők nevére rákeresve utánanézni.
|
| Előzmény: [965] Higgs, 2009-07-13 21:46:11 |
|
| [965] Higgs | 2009-07-13 21:46:11 |
 Pl. azokat amik itt vannak: http://hu.wikipedia.org/wiki/Pi
|
|
|
| [963] Higgs | 2009-07-12 19:04:51 |
 Üdv! Köszönöm a linket, hasznos volt, és felvetett egy új kérdést. A pi-vel egyenlő végtelen sorokat, hogyan lehet levezetni?
|
|
|
| [961] Higgs | 2009-07-06 13:57:02 |
 Üdv! Először is köszönöm a segítséget, de egy új kérdés merült fel bennem. A következő sor végtelen összegét hogyan lehet kiszámítani? 1/1*1+1/2*2+1/3*3+...+1/n*n Az összege pi*pi/6, de nem tudom ez, hogy jön ki.
|
|
|
| [959] R.R King | 2009-07-05 06:42:22 |
 Üdv.
Azt hiszem, hogy az általad megadott összegre nem létezik egyszerű zárt képlet. Egyébként nagyságrendet lehet mondani: az összeg nagyságrendileg kb. ln(n)
Sőt van egy olyan tétel, mely szerint az összeged-ln(n) konvergens és az Euler-konstans a határértéke
|
| Előzmény: [958] Higgs, 2009-07-05 00:47:01 |
|
| [958] Higgs | 2009-07-05 00:47:01 |
 Üdv! A következő dolog érdekel. Az 1per1+1per2+1per3+...1pern-nek mi az összege?(azért írtam így, mert máshogy nem fogadta el.)
|
|
| [957] Cuki | 2009-06-15 13:06:14 |
 Sziasztok! Csütörtökön vizsgázom, és nem igazán vagyok képben a következő feladatok megoldásával.
1. Oldjuk meg a következő lineáris programozási feladatot. x>=0,y>=0,z>=0
2x+3y+3z<=16
4x+2y+z=15
x+4y-z<=13
2x+2y+z max
2. Oldjuk meg a következő mátrixjáték-feladatot, mind az első, mind a második játékos szemszögéből. Tudjuk, hogy mind a két játékos optimális megoldásának mind a három komponense pozitív.
3 5 2
0 6 8
4 1 3
(a mátrixot nem tudtam nagy zárójelbe tenni)
Előre is köszönöm a segítséget!
|
|
| [956] Vivike | 2009-06-11 19:56:53 |
 Tegyük fel, hogy A,B,C páronként diszjunkt halmazok , |A|=kappa(nem írta ki a görög betűket);, |B|=lambde ;, |C|=mű;. Írjuk fel kappa;, lambda;, mű; segítségével a következőket! a)| A x ( B U C ) | b)| (A U B) C| A U B) felső indexben van c)| AB x BC | a B előtti A felső indexben van, a C előtti B felső indexben van
Itt meg a megoldás? Előre is köszönöm a választ!
|
|
|
|
|
| [952] nadorp | 2009-05-22 12:02:33 |
 Hacsak el nem számoltam, akkor a sajátértékek 1,3 és 5. A megfelelő sajátvektorok pedig rendre
(a,0,a),(a,0,-a),(0,a,0) ,ahol "a" tetszőleges valós szám.
Mi a "k" nálad ?
|
| Előzmény: [951] [Máté], 2009-05-22 09:31:07 |
|
| [951] [Máté] | 2009-05-22 09:31:07 |
 Sziasztok! A következő mátrixnak kellene kiszámolni a sajátértékeit és sajátvektorait. A harmadfokú egyenletet elvileg át lehet alakítani olyan formára, amiből ki lehet olvasni a sajátértékeket. Ez eddig rendben is volna, de az 5-ös miatt a szorzat egyik tagja (k-7+10/k) lesz, amiből nem lehet kiolvasni semmit. Szerintem... A segítséget előre is köszönöm.
|
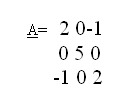 |
|
| [950] Lóczi Lajos | 2009-05-20 11:24:16 |
 Persze a Lebesgue-tétel többi feltételét is ellenőrizni kell, és a szinusz folytonosságát is használva így kijön, hogy az integrálok limesze 0.
A feladat másik részéhez azt vedd észre, hogy a "+1"-es additív tag a nevezőben eltolja a függvényt a 0-tól, így pl. [1/2,1]-en minden  esetén korlátos lesz F. esetén korlátos lesz F.
Vagyis az integrál korlátosságát elég [0,1/2]-en megnézni. Itt viszont a (-2)-odik hatványban a logaritmus fog dominálni (hiszen 0-ban + -hez tart), vagyis az 1 most elhagyható. -hez tart), vagyis az 1 most elhagyható.
Ha   0, akkor mindkét tényező korlátos, vagyis az integrál véges. 0, akkor mindkét tényező korlátos, vagyis az integrál véges.
Ha  =-1, akkor primitív függvénnyel expliciten kiszámolod, hogy az integrál véges. =-1, akkor primitív függvénnyel expliciten kiszámolod, hogy az integrál véges.
Ha   (-1,0), akkor a (-1,0), akkor a 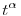 függvény kitevőben való monotonitását használva kapod, hogy az integrál véges. függvény kitevőben való monotonitását használva kapod, hogy az integrál véges.
Ha viszont  <-1, akkor használd fel, hogy a (+1 elhagyása után) a logaritmusos tényező alulról becsülhető egy tetszőlegesen kis kitevőjű t-hatvánnyal [itt lényegében a <-1, akkor használd fel, hogy a (+1 elhagyása után) a logaritmusos tényező alulról becsülhető egy tetszőlegesen kis kitevőjű t-hatvánnyal [itt lényegében a 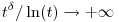 , ha , ha  >0 tetszőleges és t >0 tetszőleges és t + + limesz átrendezéséről van szó], így az integrandus alsó becslése nagyságrendileg limesz átrendezéséről van szó], így az integrandus alsó becslése nagyságrendileg 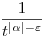 , ahol , ahol  értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen  számokra az eredeti integrál sem véges. számokra az eredeti integrál sem véges.
|
| Előzmény: [949] Cokee, 2009-05-19 23:42:43 |
|
|
|
|
| [946] Cokee | 2009-05-14 20:26:18 |
 Sziasztok!
Szeretnék segítséget kérni a következő feladatoknál:
Legyen f L1[0,1].Igaz-e,hogy L1[0,1].Igaz-e,hogy ![\sin\bigg(\frac{f(t)}{n}\bigg)\in {L^{1}}[0,1].](keplet.cgi?k=3A6C7B5E90BCCCC3) Számold ki a köv. kettős integrált: Számold ki a köv. kettős integrált: 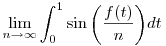
Milyen  esetén integrálható esetén integrálható 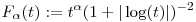 a [0,1] intervallumon? a [0,1] intervallumon?  valós szám. valós szám.
Köszi előre is Cokke
|
|
|
| [944] rizsesz | 2009-05-13 21:34:10 |
 1 helyébe írd be, hogy sin2x+cos2x, rendezz nullára, ossz le sin2x-szel (ami most nem nulla, mert akkor cosx +1 vagy -1, amelyek nem megoldások), így cosx/sinx-ben másodfokú egyenletet kapsz, ahonnan megvan cosx/sinx=ctgx.
|
| Előzmény: [943] fermel, 2009-05-13 21:14:52 |
|
| [943] fermel | 2009-05-13 21:14:52 |
 Sziasztok! A következő triginometriai egyenlet megoldásában kérném a segítségeteket:
2sinxsinx - 5sinxcosx + 7cosxcosx = 1
(Elnézést, de hiába írtam meg Wordben felső index segítségével a szögfüggvények négyzetét, egyszerűen nem másolja át abban a formában, ezért voltam kénytelen így leírni a feladatot)
Köszönöm a segítséget:
fermel
|
|





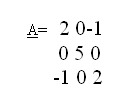
 esetén korlátos lesz F.
esetén korlátos lesz F.  -hez tart), vagyis az 1 most elhagyható.
-hez tart), vagyis az 1 most elhagyható.  0, akkor mindkét tényező korlátos, vagyis az integrál véges.
0, akkor mindkét tényező korlátos, vagyis az integrál véges.  (-1,0), akkor a
(-1,0), akkor a  >0 tetszőleges és t
>0 tetszőleges és t +
+ értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen
értékét elég kicsinek választva elérhető, hogy a nevező kitevője még mindig 1-nél nagyobb maradjon. Az ilyen hatványfüggvényekről viszont tudjuk, hogy [0,1/2]-en integráljuk divergens, tehát az ilyen  0(n
0(n