| [1008] Higgs | 2009-11-04 12:53:18 |
 Egyik hozzászólásomba oda írtam a feladat címét, és ott sincs megadva, hogy honnan jön a tömeg.
|
|
| [1007] bily71 | 2009-11-04 09:27:54 |
 Valóban, ha nem zárt a rendszer az energiamegmaradás szempontjából, akkor nem módosul a pálya.
De ezt hogy képzeljül el? Fellövünk egy rakétát, és út közben, egy másik rakétáról, mondjuk zsákokat pakolunk rá? Ha a találkozás pillanatában egyforma sebességű a zsák, és a rakéta, akkor nem változik a pálya.
Én azon az eseten gondolkoztam el, amikor a tömeg csak az összenergia rovására nőhet, és ebben az esetben a pálya módosul, hasonlóan, mint az elektron pályája is módosul a részecske gyorsítóban a relatív tömegnövekedés miatt, és nem gyorsulhat fel a "klasszikus" sebességre.
|
| Előzmény: [1005] SmallPotato, 2009-11-03 21:30:08 |
|
| [1006] Sirpi | 2009-11-04 08:52:37 |
 Szerintem is azon múlik, hogy honnan jön a plusz tömeg. Ha feltételezzük, hogy a testre rárakódó tömeg rögtön "fel van gyorsítva", azaz a megnövekedett rész is felveszi a test pillanatnyi sebességét, akkor ez a plusz tömeg nyilván nem fogja befolyásolni a test pályáját. Ha viszont a plusz tömeg nyugalmi állapotban kerül rá a testre, akkor az a sebességet csökkenteni fogja.
Az igazi gond az a feladattal, hogy ilyen váratlan tömegnövekedés nem nagyon szokott előfordulni a valóságban, ezért nehéz megfogni a dolgot.
|
| Előzmény: [1005] SmallPotato, 2009-11-03 21:30:08 |
|
| [1005] SmallPotato | 2009-11-03 21:30:08 |
 Számomra is ez tűnik teljesen kézenfekvőnek. Mégis aggályaim vannak. Ha a test tömege nő (és ez nincs befolyással a sebességviszonyokra és a pályára), akkor mozgási és helyzeti energiája egyaránt nő az eredeti tömegű állapothoz képest. Honnan származik ez az energiatöbblet?
(Bár, gyanítom, ez épp azzal a kérdéssel azonos, hogy "honnan származik a tömegnövekedés?" Végülis, ha a tömeg növekedését fedezi valami, akkor energiamegmaradás szempontjából sem zárt a rendszer.)
|
| Előzmény: [1004] Higgs, 2009-11-03 21:05:50 |
|
| [1004] Higgs | 2009-11-03 21:05:50 |
 Függőlegesen feldobott tömegpont pályája, csak a kezdősebességtől, és a rá ható gravitációs gyorsulástól függ. Ha a tömege folyamatosan nő, azzal egyenes arányban nő a rá ható gravitációs erő, vagyis a rá ható gravitációs gyorsulás állandó. Tehát a 2 eset leírása azonos. Ez jutott eszembe, bár lehet rossz.
|
|
|
| [1002] bily71 | 2009-11-03 17:59:11 |
 Ez igaz, nem vettem figyelembe, hogy nem zárt rendszerről van szó.
A függőlegesen felfelé dobott test mozgási energiája folyamatosan átalakul helyzeti energiává, tehát lassul a test.
Amikor elengedjük a testet, már nem végzünk munkát rajta, tehát van egy kezdeti mozgási energiája: 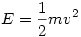 , ami állandó, ha nem hat rá erő, és függ a tömegtől, ha nő a tömeg, akkor lassul a test. , ami állandó, ha nem hat rá erő, és függ a tömegtől, ha nő a tömeg, akkor lassul a test.
Tehát a testet egyszer lassítja g, a gravitációs gyorsulás, (lassulás), mely független a test tömegétől, másodszor lassulnia kell a tömegnövekedés miatt, tehát a lassulás nagyobb mértékű, mint, ha csak a gravitációból adódna.
De ha nem jól tudom, nyugodtan javítsatok ki, nem akarok senkit félrevezetni.
De mitől nő a tömeg?
|
| Előzmény: [999] SmallPotato, 2009-11-03 14:48:05 |
|
|
|
|
| [998] bily71 | 2009-11-03 11:47:30 |
 Az impulzus megmaradás tétele szerint 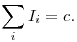 , azaz állandó, és mivel egy testünk van, ezért m1v1=m2v2. Ezek szerint, ha nő a tömeg csökken a sebesség, tehát befolyásolja a mozgást. De mitől nő a tömeg? , azaz állandó, és mivel egy testünk van, ezért m1v1=m2v2. Ezek szerint, ha nő a tömeg csökken a sebesség, tehát befolyásolja a mozgást. De mitől nő a tömeg?
|
| Előzmény: [996] HoA, 2009-11-03 11:10:31 |
|
| [997] Higgs | 2009-11-03 11:43:33 |
 Mivel a verseny véget ért, már nyugodtan kérdezhetem:D http://ortvay.mafihe.hu/2009/H09.pdf linken található az 5. feladat!
|
|
| [996] HoA | 2009-11-03 11:10:31 |
 A súlyos és a tehetetlen tömeg egyenlősége miatt nem kell, hogy befolyásolja. Persze kérdés, hogyan képzeljük a folyamatos tömegnövekedést. Mi az oka?
|
| Előzmény: [995] Higgs, 2009-11-02 21:54:04 |
|
| [995] Higgs | 2009-11-02 21:54:04 |
 Üdv!
Ha feldobok egy tömegpontot aminek a tömege folyamatosan nő, akkor ez a mozgását befolyásolja, és ha igen, miért?
|
|
| [994] béjé | 2009-11-02 18:20:42 |
 Sziasztok!
Tudna nekem valaki segíteni abban, hogy a februári és márciusi KöMaL-t hol tudnám beszerezni? Konkrétan Besenyei Ádám: A számtani-mértani közép és egyéb érdekességek I-II. c. cikkeire lenne szükségem. Előre is köszönöm.
|
|
| [993] gabor7987 | 2009-10-31 22:01:49 |
 Sziasztok a következő feladathoz szeretnék segítséget kérni:
Igazoljuk, hogy bármely 1 m m n esetén: n esetén:
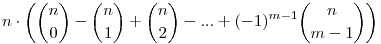
osztható m-mel!
|
|
|
| [991] Higgs | 2009-10-18 17:35:32 |
 http://mek.niif.hu/01800/01849/rtf/hatvany04.rtf
|
|
| [990] Higgs | 2009-10-18 17:23:38 |
 Üdv! A Fermat tétel-nek ismert egyszerű, esetleg elemi bizonyítása?
|
|
|
|
| [987] gabor7987 | 2009-10-16 22:19:36 |
 Egy probléma belátásához be kéne bizonyítanom, hogy (p-1)!+1 osztható p-vel, ha p egy prím. Tudna nekem ebben valaki segíteni?
|
|
|
| [985] derivált | 2009-09-17 19:14:43 |
 hellosztok nem rossz de pontosan miről is van most szó? már mint mi a feladat? :)
|
|
| [984] HoA | 2009-09-17 16:39:34 |
 Addig is egy kis segítség: Attól függ, mi az I() . Ha például x és y lineáris függvénye, mondjuk
I(x,y)=2x+3y+4
, akkor 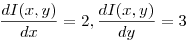 , , 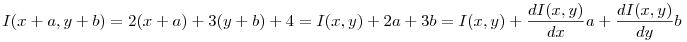 tetszőleges valós a-ra és b-re. tetszőleges valós a-ra és b-re.
|
| Előzmény: [982] pdm, 2009-09-15 02:51:10 |
|







 v2, azaz mv1
v2, azaz mv1
 m
m