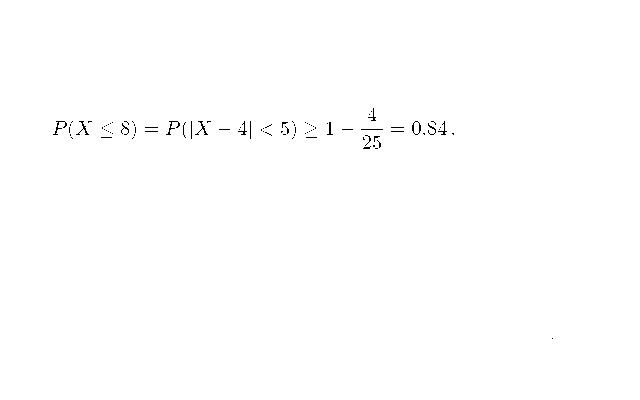| [1208] mologa | 2010-05-26 22:47:18 |
 egyes osztály:-végtelen, -1,4559 kettes osztály: -1,4559, -0.5673 hármas osztály: -0,5673, -0.3213 négyes osztály: -0,3213, -1.2099 ötös osztály: -1.2099, végtelen
Azt értem hogy az osztály közök 0.8886. De az elsö osztályközt nem értem, hogy miért 1,4559 el kezdődik? Honnan jött ez az érték? Miböl kapta?
|
| Előzmény: [1201] Fernando, 2010-05-26 21:04:55 |
|
| [1207] Fernando | 2010-05-26 21:40:30 |
 Philip J. Davis, Reuben Hersch: "A matematika élménye" című könyvében hosszan ír erről.
Felmerül Alfred Tarski neve és az axiómatikus tárgyalás - az axiómákból való formális nyelven történő levezetést már nevezhetjük bizonyításnak. Ugyanakkor ezt az eljárást -praktikus okokból- nem szokták követni még az egyetemi előadások sem. Tehát egyáltalán nem egyértelmű, hogy mit is jelent a bizonyítás. Egy matematikával foglalkozó ember nap mint nap igazol, megmutat, bizonyít állításokat, mégsem egyszerű válaszolni arra, hogy mit nevezhetünk bizonyításnak.
|
| Előzmény: [1205] RRichi, 2010-05-26 21:26:57 |
|
| [1206] Fernando | 2010-05-26 21:31:46 |
 Igen, ebben tökéletesen igazad van Róbert Gida! Én azért írtam így, mert 90 től kezdve nyilván minden használatos szinten elfogadjuk (ill. nincs okunk elvetni, ha finoman fogalmazunk).
|
| Előzmény: [1203] Róbert Gida, 2010-05-26 21:21:11 |
|
| [1205] RRichi | 2010-05-26 21:26:57 |
 Hello mindenki!
Hálás lennék, ha valaki meg tudná nekem mondani a matematikai bizonyítás teljesen percíz definícióját.
Válaszotokat előre is köszönöm!
|
|
| [1204] Fernando | 2010-05-26 21:25:16 |
 Megjegyzés: az osztályok számát úgy célszerű megválasztani, hogy a mintaelemszám és az osztályba esés valszínje szorzata -"elméleti gyakoriság"- legalább 10 legyen, különben osztályokat vonunk össze, de ezt a feladat nem kéri.
|
| Előzmény: [1202] Fernando, 2010-05-26 21:13:20 |
|
|
|
| [1201] Fernando | 2010-05-26 21:04:55 |
 Ez becsléses illeszkedésvizsgálat. Az adatokból becsüljük a feltételezett normális eloszlás paramétereit. Gyanítom, hogy valamit elírtál, uis. ilyenkor az osztályoknak mínusz végtelentől végtelenig lenne praktikus terjedniük... Leszámítva az első és utolsó osztályt az osztályközt egyenlőnek szokás megválasztani.
A minta terjedelme kb 3,5 ezért a korrigált empirikus szórással egyenlő osztályköz kb megfelel itt. Kényelmes a korrigált empirikus szórást választani osztályköznek, mert így (kicsit) könnyebb számítani az i-dik intervallum valószínűségét.
|
| Előzmény: [1199] mologa, 2010-05-26 18:03:26 |
|
| [1200] Fernando | 2010-05-26 20:22:34 |
 A k=2 eset nagyon ismert Dr. Németh József tanítványai körében. :) Nekem a legjobban Euler bizonyítása tetszik, igaz ott jónéhány lépés létjogosultsága kérdéses. Németh József: Előadások a végtelen sorokról (Polygon): ebben olvasható vagy három biz.
|
| Előzmény: [1173] D. Tamás, 2010-05-20 19:08:29 |
|
| [1199] mologa | 2010-05-26 18:03:26 |
 Igazolja, hogy a minta normális eloszlású Adja meg a khi2 statisztika értékét ha az osztályok száma öt?
-1.48 , -1.48 , -1.45 , -1.06 , -1.05 , -1.04 , -1.04 , -0.94 , -0.94 , -0.75 , -0.70 , -0.55,-0.53 -0.48 , -0.38 , -0.09 , -0.05 , 0.04 , 0.05 , 0.11 , 0.18 , 0.19 , 0.32 , 0.36 , 0.48 , 0.51 , 0.60 0.70 , 0.70 , 0.83 , 1.30 , 1.50 , 2.08
minta elemszáma n = 33 átlag= -0,123 osztályok száma r=5 egy osztály szélessége Scsillag=0.8886 Scsillag= korrigált tapasztalati szórás :)) Az osztály szélességre miért a korrigált tapasztalati szórást veszi?
Osztály közök minusz végtelen-1.4559 -1,4559, -0,5673 -0,5673, -0,3212 -0.3212, -1,2099 -1,2099, minusz végtelen
Az osztály közök miért igy alakultak? Ezt nem értem:)
|
|
| [1198] mologa | 2010-05-26 16:58:47 |
 Sirpi elküldtem neked emailbe :)
|
|
| [1197] mologa | 2010-05-26 16:51:34 |
 uhhhh ez össze vissza mászott :))
|
|
| [1196] mologa | 2010-05-26 16:49:44 |
 2. Igazolja, hogy a minta normális eloszlású Adja meg a khi2 statisztika értékét ha az osztályok száma öt?
-1.48 , -1.48 , -1.45 , -1.06 , -1.05 , -1.04 , -1.04 , -0.94 , -0.94 , -0.75 , -0.70 , -0.55,-0.53 -0.48 , -0.38 , -0.09 , -0.05 , 0.04 , 0.05 , 0.11 , 0.18 , 0.19 , 0.32 , 0.36 , 0.48 , 0.51 , 0.60 0.70 , 0.70 , 0.83 , 1.30 , 1.50 , 2.08
minta elemszáma n = 33 A becsült paraméterek (átlag)=-0.123 korrigált szórás S csillag= 0.8886 Az osztályok száma r = 5
Egy osztály szélessége S csillag= 0.8886 Az osztály szélességre miért a (szórást) 0.8886 ot veszi?
Osztály közök Pi nPi
- - 1.4559 2 0.0668 2.2044 0.0190
-1.4559, -0.5673 9 0.2417 7.9761 0.1344
-0.5673, -0.3213 12 0.3830 12.639 0.0323 -0.3213, -1.2099 7 0.2417 7.9761 0.1195
-1.2099, - 3 0.0668 2.2044 0.2871 khi2=0.5893 Az osztályközök értéki miért igy jöttek ki? Ezt nem értemL Valaki levezeti
|
|
|
| [1194] mologa | 2010-05-26 16:40:15 |
 Sajnos nem tudom bemásolni a word-ben irt feladatot. Mig TeX-ben irnám meg kirügyeznék:))
|
|
|
|
|
| [1190] Hölder | 2010-05-23 23:49:40 |
 Sziasztok! Azon gondolkodtam el,hogy ha 2(n)+1 prim (kitevőben van az n), akkor n kettő hatvány (Fermat primek),de forditva igaz -e, azaz, ha n kettőhatvány,akkor 2(n)+1 prim, megnéztem egy jó ideig,addig igaz volt,az a sejtésem, hogy nem az.
|
|
|
|
|
|
| [1185] jonas | 2010-05-21 11:56:08 |
 A Poisson közelítést a binomiális eloszlásra akkor lehet használni, ha várhatóan kevés rossz üveg készül, például abban az esetben, amit Sirpi javasolt.
|
| Előzmény: [1182] Yvi, 2010-05-20 23:38:21 |
|
| [1184] Maga Péter | 2010-05-21 11:43:15 |
 A páros esetben  (2k)= (2k)= 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen  (3), (3), (5),... a kérdéses értékek, ezek tetszőleges pontossággal kiszámolhatók, akár a (5),... a kérdéses értékek, ezek tetszőleges pontossággal kiszámolhatók, akár a  , az e, a , az e, a  (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a  páratlan értékei, illetve ha nem, akkor esetleg más konstansokkal ( páratlan értékei, illetve ha nem, akkor esetleg más konstansokkal ( , e stb.) összefüggésbe hozhatók-e. A , e stb.) összefüggésbe hozhatók-e. A  -ról sem tudjuk, hogy racionális-e, és azt sem tudjuk, hogy -ról sem tudjuk, hogy racionális-e, és azt sem tudjuk, hogy  +e racionális-e (ha az lenne, akkor az e ugyanúgy kifejezhető lenne a +e racionális-e (ha az lenne, akkor az e ugyanúgy kifejezhető lenne a  -ből, mint a -ből, mint a 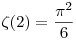 ), mégsem használjuk egyikre sem, hogy nem ismert. ), mégsem használjuk egyikre sem, hogy nem ismert.
|
| Előzmény: [1176] jenei.attila, 2010-05-20 19:36:13 |
|
|
| [1182] Yvi | 2010-05-20 23:38:21 |
 A binomiális eloszlással hogy jött ki a 803? Tényleg nem Poisson, csak elnéztem, az volt, oda írva, hogy a Poisson közelítést kell használni. Ez jelenti azt, hogy np=lambda?
|
| Előzmény: [1177] jonas, 2010-05-20 21:39:13 |
|
| [1181] jonas | 2010-05-20 22:57:29 |
 Persze nem kell nagyon komolyan venni ezt a tankönyvi példát, mert a válasz nagyon érzékeny az adatokra, mint pl. a szórás pontos értékére, a sör mennyiségének az eloszlására, meg az egyes üvegek függetlenségére. Ha egy kicsit módosítod a számokat, kaphatsz 0.1-et vagy 0.999-et is eredménynek.
|
| Előzmény: [1180] jonas, 2010-05-20 22:51:22 |
|
|
| [1179] Sirpi | 2010-05-20 22:40:07 |
 Szerintem el lett írva az átlag (51 helyett 50 kellene), mert úgy szimmetrikus a két határszám (48,9 és 51,1). És úgy valószínűleg értelmes lesz az eredmény is, ami kijön.
|
| Előzmény: [1177] jonas, 2010-05-20 21:39:13 |
|
| [1178] Higgs | 2010-05-20 22:20:09 |
 http://www.newscientist.com/article/dn18886-impossible-motion-trick-wins-illusion-contest.html
A valóságban is ezt a hatást keltené?
|
|
| [1177] jonas | 2010-05-20 21:39:13 |
 Ezt két lépésben kell megoldani. Először azt kell kiszámítani, hogy egy üveg sör mikor lesz hibás.
Annak a valószínűsége, hogy 48.9-nál kevesebb sör van az üvegben, elhanyagolhatóan kicsi, viszont mivel az átlag közel van, az 51.1-nél több sörnek egy üvegnél kb. 0.401 a valószínűsége. (Itt nyilván azt tettük föl, hogy a sör űrtartalma normális eloszlású.)
Ezért aztán a napi 2000 üvegből átlagosan 803 hibás van, tehát a binomiális eloszlást nem Poisson, hanem normális eloszlással kell közelíteni. Annak a valószínűsége, hogy 20-nál kevesebb túl nagy üveg sör készül, e miatt nagyon kicsi (értsd: előbb romlik el a gép), ha jól számolok, akkor 5.10-556 nagyságrendű.
(Nem vagyok túl jó statisztikából, úgyhogy valaki ellenőrizze a számításaimat.)
|
| Előzmény: [1175] Yvi, 2010-05-20 19:17:32 |
|
| [1176] jenei.attila | 2010-05-20 19:36:13 |
 A első probléma a Bernoulli-féle hatványösszeg probléma, amelyre egy nagyon szép levezetést találhatsz pl. Dörrie A diadalmas matematika c. könyvében. Egyébként magad is könnyen levezetheted, ha feltételezed, hogy a k-adik hatványok összege n-nek (a tagszámnak) egy k+1-ed fokú polinomja. Ekkor a polinomot határozatlan együtthatókkal felírva, n helyére 1,2,...k+2-őt helyettesítve, egy lineáris egyenletrendszert kapsz az együtthatókra. Az hogy a zárt képlet n-nek k+1-ed fokú polinomja, könnyen látható abból, hogy pk(n+1)-pk(n)=nk (ahol pk(n) a zárt alak n tagra) egy k-ad fokú polinom. Márpedig egy k+1-ed fokú polinom két egymás melletti természetes számon felvett helyettesítési értéke k-adfokú polinom. Tehát ha a fenti egyenletrendszernek van megoldása, akkor az megadja a zárt képletet is. Ennél egy lényegesen szellemesebb levezetést találsz az említett könyvben. A második probléma jóval nehezebb, és semmi köze az elsőhöz. Tudomásom szerint páros k-kra ismert zárt alak (k=2-re Euler adta meg először), míg páratlanokra nem ismert (ha nem így van, nyugodtan javítsatok ki).
|
| Előzmény: [1173] D. Tamás, 2010-05-20 19:08:29 |
|
| [1175] Yvi | 2010-05-20 19:17:32 |
 Köszönöm a segítséget, itt van egy utolsó példa, nagyon hálás lennék ha arra is elmondaná a megoldást valaki, aztán már abba is hagytam: Ha egy gép napi 2000 üveg sört gyárt, akkor mi a valószínűsége, hogy a nem 48.9 és 51.1 cl sört tartalmazó üvegekből maximum 20 készül el egy napon. (átlag: 51 cl és szórás: 0.4 cl, de nem tudom, hogy ezekre az adatokra szükség van-e? A feladatgyűjtemény mindenesetre azt írja, hogy ez Poisson-eloszlás)
|
| Előzmény: [1172] leni536, 2010-05-20 14:57:55 |
|
|
| [1173] D. Tamás | 2010-05-20 19:08:29 |
 Felmerült bennem a következő probléma: Több összeg meghatározásánál nagyon jól jönnek az ún. véges számsorok összegei. Például a számtani sorozat 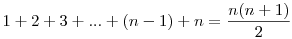 vagy az első n négyzetszám összege vagy az első n négyzetszám összege 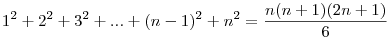 illetve ismertnek számít még a illetve ismertnek számít még a 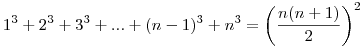 összefüggés is. összefüggés is.
És persze még folytathatnánk a sort, de jogosan merül föl a kérdés, hogy miképpen lehetne felírni az 1k+2k+3k+...+(n-1)k+nk összeget n függvényében. Ez lenne először is a legelső kérdésem, mert szerintem az algebrában biztosan egy kivesézett téma, de mégsem találtam hozzá forrást egy könyvben sem erről. Sajnos amilyen bizonyításokat ismerek ezekre az összefüggésekre, azokban mindig tettünk egy észrevételt, s miután "kiokoskodtuk" a helyes összefüggést teljes indukcióval beláttuk, így n-re ez nem teljesen használható. A következő ami szorosan kapcsolódik ehhez, az a reciprokösszeg. Tehát ha tekintjük az 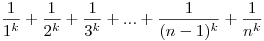 összeget, akkor mi a sorozat határértéke, ha k összeget, akkor mi a sorozat határértéke, ha k N? k=1 esetén ismert a probléma, ekkor a határértéke N? k=1 esetén ismert a probléma, ekkor a határértéke  , illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték , illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték 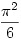 . No de hogyan lehetne felírni a határértéket k függvényében? . No de hogyan lehetne felírni a határértéket k függvényében?
|
|
| [1172] leni536 | 2010-05-20 14:57:55 |
 X N(64,162) N(64,162)
Ez ugye egy pontszám alakulásának a valószinűségi változója. Tudjuk, hogy egy diák 0,1 valószínűséggel bukik meg. Legyen x0 a bukás ponthatára, így:
P(X<x0)=0,1
Standardizálva az X-et:
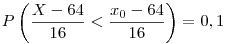
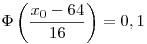
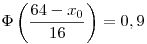
A standard eloszlást táblázatából:
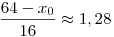
x0 43,52 43,52
Tehát jó közelítéssel 43 ponttal még buknak, 44-gyel már nem.
|
| Előzmény: [1171] Yvi, 2010-05-20 13:25:08 |
|
| [1171] Yvi | 2010-05-20 13:25:08 |
 Nagyon köszönöm, ha lehet, itt van még egy feladat ami nagyon nem megy: Egy osztály teszteredményeinek normál eloszlásának átlaga 64, szórása 16. Találja meg a legkisebb osztályzatot, ami még nem jelent bukást, hogyha a legrosszabb 10százalék bukik meg. Ezt meg próbáltam kiszámolni, hogy 1-P(X<x)=0.1 de valamit biztos elrontottam,mert mínusz érték jött ki. b.) feladat: Ha minden diák 60 és 70 pont között hármast kapott, és tudjuk, hogy pontosan 10 diák kapott hármast, hány diák írta meg a tesztet?
|
|
| [1170] Maga Péter | 2010-05-20 08:36:57 |
 Egy egész szám 5-nél kisebb távolságra van a 4-től pontosan akkor, ha nemnegatív, és legfeljebb 8. Innen az 5. A Csebisev' elvben csak azt engedné meg, hogy 4-et írj, de az egészértékűség miatt ezt fel tudod nyomni 5-re, és így erősebb becslést kapsz.
|
| Előzmény: [1169] Yvi, 2010-05-20 02:24:57 |
|
| [1169] Yvi | 2010-05-20 02:24:57 |
 Sziasztok, lenne egy valszám feladat amit nem értek: Egy telefonközpont napi 2000 hívást kap,annak a valószínűsége,hogy egy hívás téves, az 0.002.(független események) Mi a valószínűsége annak, hogy a 2000ből maximum 8 hívás téves? A megoldókulcs szerint ez binomiális eloszlás, illetve utána Csebisev egyenlőtlenséget kell használni. Ami leginkább nem világos, hogy mi az az 5 ott? (Elnézést, hogy ilyen halványak a vonalak, azért remélem látszik a lényeg)
|
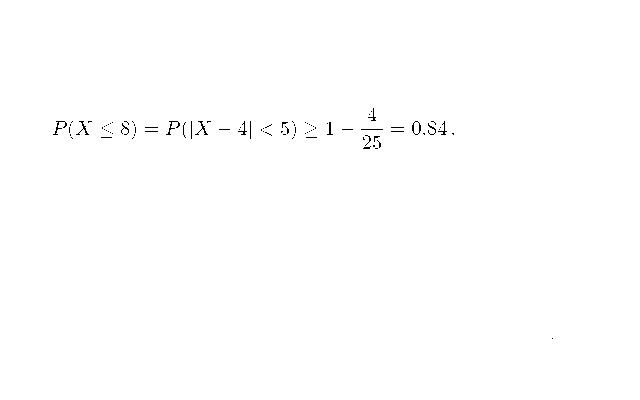 |
|
| [1168] Fernando | 2010-05-19 22:52:58 |
 Egyébként nyugi, maga Student (akit persze nem Studentnek hívtak:) is elszámolta annak idején az eloszlást.
Dolgozatban lineáris interpoláció a táblázati értékekre és kész.
Persze meg lehet próbálni definíció szerint is kiszámolni, vagy inkább kiszámoltatni számítógéppel és akkor kiderül, hogy mennyi az annyi. :)
|
| Előzmény: [1146] mologa, 2010-05-17 18:35:14 |
|
| [1167] Sirpi | 2010-05-19 11:46:44 |
 FF
(Egyébként nem tudod a win2000-et virtuális operációs rendszerként futtatni? Mert használhatnál fő oprendszerként bármit, amit szeretnél, és csak a speckó programodhoz, ami igényli a win2000-et, indítanád el a virtuális gépet.)
|
| Előzmény: [1166] HoA, 2010-05-19 10:57:33 |
|
| [1166] HoA | 2010-05-19 10:57:33 |
 Egyik gépepen meg kell tartanom a Windows2000 op. rendszert. Az Internet Explorer viszont már nem jó például a youtube-hoz. Hogy ne kelljen sokat kisérletezgetnem, tudja valaki, van-e olyan böngésző, ami megfelel az új követelményeknek és Windows2000 alá telepíthető?
|
| Előzmény: [1161] Róbert Gida, 2010-05-18 10:03:48 |
|
| [1164] Fernando | 2010-05-18 16:35:57 |
 Bár azt gondolom, hogy a pszichológiai szempontból pontatlan volt amit írtál, de ez mit sem változtat a dolog igazságtartalmán. Persze a dolog messzire vezetne nagyonis.
Röviden szólva a társadalom egyszerűen nem áll a tanárok mögött.
|
| Előzmény: [1162] bily71, 2010-05-18 11:02:52 |
|
| [1163] SmallPotato | 2010-05-18 13:38:38 |
 Na jó ... azért a helyzet nem ennyire egyszerű. Normális oktatás ma is van. A (vélt vagy valós) demokrácia ugyan kissé sajátossá tette a viszonyokat - de a jelen esetben inkább a tapasztalatból adódó különbségről beszélhetünk.
(Lásd HoA - jogos - észrevételét a fiatal versenyző elriasztásával kapcsolatosan. :-) )
|
| Előzmény: [1160] mologa, 2010-05-18 08:46:23 |
|
| [1162] bily71 | 2010-05-18 11:02:52 |
 A régi időkben az oktató egyik hatásos eszköze a fegyelmezés volt, mely része a nevelésnek, ugyanúgy, mint az oktatás. A mai törvények ezt az eszköszt kivették a tanárok és a gyámhivatal kezéből és olyan jogokkal ruházzák fel a gyermekeket, melyek egyszerűen nem illetik meg őket.
|
| Előzmény: [1161] Róbert Gida, 2010-05-18 10:03:48 |
|
|
|
| [1159] HoA | 2010-05-18 08:37:48 |
 Ne riaszd el a fiatal versenyzőt ha ilyen problémái vannak.
Lineáris kapcsolatot feltételezve ha a szabadságfok 40-ről 30-ra változik az érték pedig 21 ezrelékkel nő, akkor a 40 --> 37 változáshoz ennek 3 tizede , azaz 6,3 ezrelék , a táblázat pontosságát figyelembe véve kerekítéssel 6 ezrelék tartozik, így a keresett érték 2,027.
|
| Előzmény: [1157] SmallPotato, 2010-05-17 22:17:44 |
|
| [1158] SmallPotato | 2010-05-17 22:38:22 |
 A táblázati értéktől való eltérés két okból adódhat: egyrészt a közrefogó adatok pontossága véges (magyarán pl a 2,042 elvileg lehet akár 2,0415 vagy efféle és a 2,021 is lehet 2,0205, másrészt az összefüggés nem egészen lineáris (a 2,042 környékén láthatólag nagyobbak a lépések, mint a 2,021 környékén).
|
| Előzmény: [1157] SmallPotato, 2010-05-17 22:17:44 |
|








 (3) rac. együtthatós polinomjaként kifejezhető páratlan k-kra is
(3) rac. együtthatós polinomjaként kifejezhető páratlan k-kra is 
 2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen
2k*q, ahol q racionális szám, és effektíve kiszámolható minden konkrét esetben. A páratlan k-król tennék kiegészítést, kicsit pontosítom a ,,nem ismert'' kifejezést (nem kötekedésképp!!). A problémát megkerülve egyszerűen  (Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a
(Euler-konstans). Amit nem tudunk, az az, hogy racionálisok-e a 
 N? k=1 esetén ismert a probléma, ekkor a határértéke
N? k=1 esetén ismert a probléma, ekkor a határértéke  , illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték
, illetve kevésbé ismert még az az összefüggés, hogy k=2 esetén a határérték 
 N(64,162)
N(64,162)  43,52
43,52