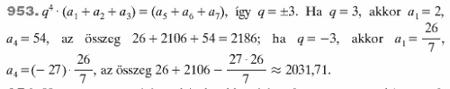|
| [1358] Fannka | 2010-09-20 21:19:19 |
 Hát mindenesetre köszönöm a válaszokat! És nincs semmi problémám azzal, h házit kell csinálnom, sőt kifejezetten jó feladatok ezek:) Nem lustaságból írom fel ide, pusztán ciki lenne nem megoldani a feladatot, meg a többiek is számítanak rám... A 7végén sokat gondolkodtam rajta, és nem jutottam semmire... Az órai feladatokat értem, sőt java részét magamtól is megoldom, de azok közt nincs (vagy én nem látok) ezekhez hasonló. De attól még ugyanúgy gondolkodom ezeken, mert vannak kevésbé izgi órák, amiket ennek szentelek:P Szóval akkor bocs, h ilyenekkel botránkoztattam meg itt a segítőkész embereket, ezentúl megtartom magamnak a kérdéseim. (Ui.: Milyen logika az, h azok tartanak össze, akiknek kutya a szimbólumok?)
|
 |
|
|
|
| [1355] Róbert Gida | 2010-09-20 20:43:26 |
 Nem látom, hogy miért ne vizsgálhatnánk, hogy rac. vagy irrac. Abban igazad van, hogy irrac csak úgy lehet, ha végtelen sok ikerprím van (amit sejtünk), de rac. nem csak úgy lehet, ha véges sok ikerprím van, hiszen egy végtelen sok tagú poz. sor összege is lehet rac: 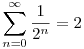
|
| Előzmény: [1350] bily71, 2010-09-20 17:03:25 |
|
| [1354] Sirpi | 2010-09-20 20:26:15 |
 Mivel ez nem egy fizikapélda, nem különösebben. Szerintem amúgy is zavaróbb, hogy nincs végtelen sok atom a világegyetemben a kapott szám megjelenítéséhez. Ez csak egy szemléltetés, hogy hogy lehet ilyesmit elképzelni, de a valóságban nyilván senki nem fog nekiállni ilyet játszani.
|
| Előzmény: [1348] Róbert Gida, 2010-09-20 15:29:43 |
|
| [1353] bily71 | 2010-09-20 19:25:18 |
 Valóban, nem szerepel az összes rac. illetve irrac. szám. Azt én is tudom, hogy nincs, (Cantor bizonyitása nem olyan bonyolult, hogy ne érteném), csak játszom a gondolattal.
Képezzünk egy fát a következőképp: az első csúcsot cimkézzük fel a 0-val. Az első csúcsból induljon 10 él 10 csúcsba, cimkézzük fel az új csúcsokat a 0-tól 9-ig terjerdő természetes számokkal, úgy, hogy a baloldali kapja a 0-t, a mellette lévő az 1-est, és igy tovább, vagyis mindegyik új csúcs különböző számú cimkét kapott. Az új csúcsok mindegyikéből induljon 10 él 10 új csúcsba, ezeket a csúcsokat is az előbbiekhez hasonlóan cimkézzük fel. Azután ezekből a csúcsokból is induljon..., és igy tovább
Ime, itt van az összes [0,1] intervallumba eső valós szám, ugyanis, ha elindulunk a kezdőcsúcstól, végigmegyünk valamelyik úton és leirjuk egymás után, hogy melyik számokat érintettük, úgy, hogy az első 0 után egy tizedesvesszőt irunk, akkor egy valós számot kapunk. Ha csak 0-kat , akkor a 0-t, ha csak 9-eseket érintünk, akkor az 1-et kapjuk eredményül. (A 0-n és az 1-en kivül minden racionálist kétszer kaptunk meg, pl.: 0.5999...=0.6.)
Megszámlálható-e bejárható utak halmaza?
|
| Előzmény: [1352] Alma, 2010-09-20 18:04:29 |
|
|
| [1351] bily71 | 2010-09-20 17:51:27 |
 Tudjuk, hogy az irracionális számok többen vannak, mint a racionálisok. Azt is tudjuk, hogy bármely két különböző irrac. szám között van legalább egy rac. szám és forditva.
Legyenek a,b Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c Q, vagyis rac szám úgy, hogy a<c<b. Ekkor létezik a', a' Q, vagyis rac szám úgy, hogy a<c<b. Ekkor létezik a', a' Q*, c<a'<b. Ekkor létezik c', c' Q*, c<a'<b. Ekkor létezik c', c' Q, a'<c'<b. Ekkor... Q, a'<c'<b. Ekkor...
Képezzünk ezekből a számokból párokat úgy, hogy az első szám rac., a második irrac. legyen: (0,b), (c,a), (c',a'),...! Úgy tünik, hogy akárhányszor egy új irrac. számot veszünk a régiek mellé, mindannyiszor kapunk egy új rac. számot is.
Ezekszerint mégis van bijektiv leképezés a két halmaz között?
|
|
| [1350] bily71 | 2010-09-20 17:03:25 |
 Eszembe jutott egy régebbi vitánk a Brun-állandóról. Továbbra is fenntartom, hogy amig nem tudjuk, hogy az ikerprimek száma véges-e, avagy végtelen, addig felesleges, sőt butaság vizsgálni a Brun-állandó racionális, vagy irracionális voltát. Egy sorozat összegéről csak akkor tételezetjük fel, hogy irracinális, ha már tudjuk, hogy az végtelen sok tagból áll.
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
| [1349] bily71 | 2010-09-20 16:49:38 |
 Mondjuk B első számjegye 1, a második 4, a harmadik 1,... vagyis B a  soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta. soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta.
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
|
| [1347] jonas | 2010-09-20 15:27:34 |
 Hmm, akkor most már én is mondok igazi segítséget. Fannka: a házi feladatokhoz általában segít valamelyik korábbi (órai vagy házi) feladat. Nézd át az előző heti feladatsort, és a megoldásokat, és találd ki, melyik kettő illik ide. Ha nem tudod a megoldást a megfelelő feladatokra, akkor próbáld meg először azokat megoldani; ha nem megy, kérdezz meg valakit, aki bent volt az órán, és jegyzetelt. (Nagy általánosságban a nők jobban jegyzetelnek az egyetemi órákon, mint a férfiak, de sok egyéni különbség van.)
|
| Előzmény: [1346] Sirpi, 2010-09-20 15:20:55 |
|
| [1346] Sirpi | 2010-09-20 15:20:55 |
 Képzeld azt, hogy az első számjegyet 1/2, a 2.-at 1/4, a 3.-at 1/8, stb. másodperc alatt írják a szám végére (mindig feleződik az idő). Ekkor 1 másodperc után elő is áll a végeredményként kapott szám. És ha B nem onnan kapta a nevét, hogy hihetetlenül B-na, akkor nagyon könnyen el tudja érni, hogy ez irracionális legyen (egyelőre nem lövöm le).
|
| Előzmény: [1342] bily71, 2010-09-20 14:51:06 |
|
|
| [1344] HoA | 2010-09-20 14:57:53 |
 Arra gondolsz, hogy ne mi oldjuk meg a házi feladatait? Ha igen, akkor amit leírtam, ugyanúgy csak segítség, mint a javaslat az 1 kút, 2 kút, stb. megközelítéshez. A bizonyításhoz igazolni kell a grafikon említett tulajdonságait.
Vogel hozzászólásából nem látom, miért ne adhatnánk ötleteket, hisz ő is ad, meg te is. Vagy másra gondoltál? Lehet, hogy tudnom kéne, mi az az fmx ?
|
| Előzmény: [1341] jonas, 2010-09-20 14:37:24 |
|
|
| [1342] bily71 | 2010-09-20 14:51:06 |
 J-nek van nyerő stratégiája, ugyanis ahhoz, hogy ez a szám irracionális legyen végtelen sok tizedesjegyet kell leirni, vagyis a játék sosem ér véget. Ha eltekintünk attól az apróságtól, hogy az ember élete véges és vég nélkül folytatódik a játék, B akkor sem nyerhet, mert akárhányadik lépésnél is tart, a tizedesjegyek száma mindig véges.
|
| Előzmény: [1340] jonas, 2010-09-20 14:27:57 |
|
| [1341] jonas | 2010-09-20 14:37:24 |
 HoA, csak azért segítsz neki, mert ő is kutya fényképeket rak föl, vagy pedig nem láttad, hogy vogel mit írt? Csak kíváncsiságból kérdezem.
|
| Előzmény: [1339] HoA, 2010-09-20 12:12:42 |
|
|
| [1339] HoA | 2010-09-20 12:12:42 |
 Erre a feladatra van egy egyszerű, szemléletes megoldás, ha már szóba került leírom: Képzeljünk az autóra egy póttankot, az egész pályára elegendő benzinnel. Valamelyik kúttól indulva rajzoljunk egy grafikont, ami az autóban lévő benzin mennyiségét mutatja a megtett út függvényében. Az induló kútnál megugrik a kút tartalmával, utána a következő kútig egyenletesen csökken, itt megint helyben nő ennek a kútnak a tartalmával, és így tovább. Egy fűrészfogazás jellegű ábrát kapunk. A feltétel miatt a kiinduló kúthoz visszaérve pont annyi benzin lesz az autóban, mint induláskor. Lehet, hogy lesznek olyan pontok, ahol a benzin a kezdeti szint alatt van, vagyis a póttankból fogyasztunk.
Nézzük meg, hogyan változik a grafikon, ha egy másik kúttól indulunk. A menete ugyanaz, csak függőlegesen el lesz tolva, felefelé vagy lefelé - és persze az elejéről egy darab a végére kerül. A megoldás: A tetszőleges kúttól induló grafikonon válasszuk ki a legmélyebb pontot. Ez nyilván valamelyik kúthoz történő érkezésnél van. Ettől a kúttól indulva a grafikon végig a póttank szintje felett halad, a póttank elhagyható.
|
| Előzmény: [1335] Fannka, 2010-09-19 21:06:18 |
|
|
| [1337] Fannka | 2010-09-19 22:35:44 |
 szabad tudnom ki vagy, Vogel?:P már csak azért is h tudjam, ki tengeti a vasárnap estéit rajtam kívül KöMaL fórumon:) meg h mennyire égtem le itt...
|
 |
|
| [1336] vogel | 2010-09-19 21:27:52 |
 Először vizsgáld meg 1 kútra, 2 kútra... 2 kút esetén el lehet indulni egy kútból úgy, hogy tovább mehess egy másik kúthoz? Stb. Ha semmiképp sem megy, inkább konzultálj/gondolkodj a társaiddal az fmx (:-P) házikról, mert mindenre nem fogsz itt választ kapni.
|
| Előzmény: [1335] Fannka, 2010-09-19 21:06:18 |
|
| [1335] Fannka | 2010-09-19 21:06:18 |
 Egy kör alakú autópálya mentén benzinkutak vannak, bennük különböző mennyiségű benzin. Tudjuk, hogy összesen pont annyi benzin van szétosztva a kutak közt, amennyi egy kör megtételére elég. Bizonyítsuk be, hogy van olyan pontja a pályának, ahonnan egy autó üres tankkal elindulva végig tud menni a kutakban található benzin segítségével.
|
 |
|
|
| [1333] Fannka | 2010-09-19 20:43:13 |
 J És B felváltva írnak a tizedesvessző után számjegyeket végtelen sokáig. J nyer, ha a kapott szám racionális, B ha irracionális. Kinek van nyerő stratégiája? (ui: és köszi az előző megoldásokat:)
|
 |
|
|
| [1331] tamas553 | 2010-09-19 12:14:42 |
 Van két kitérő egyenesünk a térben:
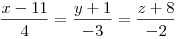

Mekkora a két egyenes távolsága?
|
|
| [1330] Kristóf Miklós 2 | 2010-09-18 16:33:47 |
 Kedves Jonas, köszönöm kedves válaszod, végre láttam egy egyszerűbb megoldást. Nekem ennél bonyolultabb jött ki. Bizonyára azért olyan népszerű, mert egyszerűen megfogalmazható, mégse egyszerű a megoldás.
|
| Előzmény: [1329] jonas, 2010-09-17 11:26:31 |
|
|
| [1328] Kristóf Miklós 2 | 2010-09-17 09:51:37 |
 Kedves Mindenki! Van egy aranyos feladatom, amit szeretnék megosztani veletek.
Van egy r sugarú legelő, és az egyik széléhez ki van kötve egy kecske. A kötél hossza R. A kecske mindent lelegel, amit elér. Milyen hosszú a kötél, ha a kecske a legelőnek épp a felét legeli le?
Adjuk meg 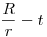 10 jegy pontosan! 10 jegy pontosan!
|
|
| [1327] jonas | 2010-09-16 17:09:58 |
 Én meg tudom csinálni n+1 lakattal is, bármi legyen is a k.
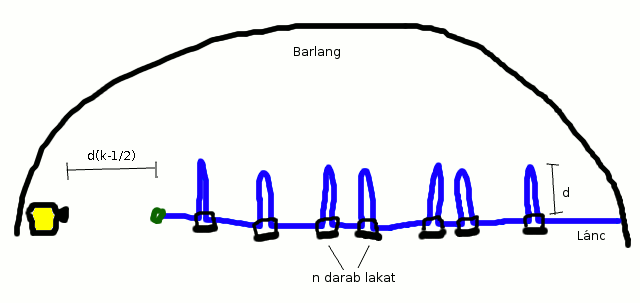
Rögzítsük a barlang egyik oldalához a kincsesládát, ezen legyen egy lakat. A lakat kulcsát rögzítsük egy hosszú láncra a barlang másik végéhez. A láncot n darab lakattal rövidebbre vesszük úgy, hogy minden rablóhoz pontosan egy lakatja van, és ehhez csak neki van kulcsa. Minden lakat két, egymástól d távolságra lévő láncszembe van beakasztva, és a lefogott d hosszú darabok nem fedik át egymást. A lánc hossza úgy van beállítva, hogy ha k lakatot kinyitnak, akkor már a végén lévő kulcs eléri a kincsesláda lakatját, de ha csak k-1-et nyitnak ki, akkor nem.
|
 |
| Előzmény: [1326] Róbert Gida, 2010-09-16 15:54:30 |
|
| [1326] Róbert Gida | 2010-09-16 15:54:30 |
 Még ennél is van jobb, ha nem egy szimplán leüthető lakatról van szó, hanem egy elektronikusról. Legyen N egy nagy pozitiv egész szám, a kulcs ami a széfet nyitja pedig egy random [N/2,N) intervallumba eső R egész. Az i-edik alkalmazott kulcsa az Rmod pi szám, ahol 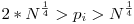 és pi prím (különbözőek). Bármely 4 összeáll, akkor ki tudják nyitni a zárat a kínai maradéktétel miatt (az elektronikus zár kiszámolja R-et a kínaiból), de bármely 3 még nem. és pi prím (különbözőek). Bármely 4 összeáll, akkor ki tudják nyitni a zárat a kínai maradéktétel miatt (az elektronikus zár kiszámolja R-et a kínaiból), de bármely 3 még nem.
|
| Előzmény: [1325] jonas, 2010-09-16 13:30:35 |
|
| [1325] jonas | 2010-09-16 13:30:35 |
 Az a feladat ide csak alsó becslést ad. A felső becslése csak arra az esetre vonatkozik, amikor minden zár közvetlenül az egy páncélszekrény ajtaján van.
Bizonyos n,k értékekre jobb konstrukciót lehet adni, ha használhatsz plusz ládákat. (Lehet, hogy az is segíthet, ha csak egy ládád van, de sorba köthetsz lakatokat esetleg láncot is használva, nem tudom.)
Mondok egy példa konstrukciót. Minden (t,v) számpárhoz, ahol 0 t t w w n egészek, vegyünk fel egy L(t,w) ládát, amibe majd néhány kulcsot rejtünk. Azt szeretnénk, hogy L(t,w)-t pontosan akkor lehessen kinyitni, ha együttműködik az R(0),R(1),...,R(w-1) rablók közül legalább t fő, meg még az R(w) rabló. Ezt az általános esetben úgy érjük el, hogy az L(t,w) ládán két lakat van, az elsőhöz csak az R(w) rablónak van kulcsa, a másikhoz viszont az L(t-1,t-1),L(t-1,t),...,L(t-1,w-1) ládák mindegyikébe rakunk egy kulcsot. Speciálisan azonban ha 0=t, akkor csak az első lakat legyen a ládán. Végük a kincset rakjuk egy külön ládába, és az ezen lévő egy lakathoz az L(k-1,k-1),L(k-1,k),...,L(k-1,n) ládába rejtsük. n egészek, vegyünk fel egy L(t,w) ládát, amibe majd néhány kulcsot rejtünk. Azt szeretnénk, hogy L(t,w)-t pontosan akkor lehessen kinyitni, ha együttműködik az R(0),R(1),...,R(w-1) rablók közül legalább t fő, meg még az R(w) rabló. Ezt az általános esetben úgy érjük el, hogy az L(t,w) ládán két lakat van, az elsőhöz csak az R(w) rablónak van kulcsa, a másikhoz viszont az L(t-1,t-1),L(t-1,t),...,L(t-1,w-1) ládák mindegyikébe rakunk egy kulcsot. Speciálisan azonban ha 0=t, akkor csak az első lakat legyen a ládán. Végük a kincset rakjuk egy külön ládába, és az ezen lévő egy lakathoz az L(k-1,k-1),L(k-1,k),...,L(k-1,n) ládába rejtsük.
Ezzel a megoldással elég összesen O(n2) láda, O(n2) lakat és O(n3) kulcs. Ez megfelelő n,k esetén olcsóbb lehet, mint a megoldásban leírt 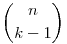 lakat. lakat.
(Arra vigyázni kell, hogy a ládák elég nehezek legyenek ahhoz, hogy ne lehessen ellopni őket. Vegyük viszont észre, hogy a megadott séma robosztus abban az értelemben, hogy k-nál kevesebb rabló nem tudja kulcsok ellopásával megakadályozni azt, hogy rablóknak másik, az előbbitől diszjunkt halmaza kinyithassa a ládát, így a kulcsokat nem szükséges a ládák belsejéhez láncolni.)
|
| Előzmény: [1324] Maga Péter, 2010-09-16 10:10:38 |
|
|
| [1323] Fannka | 2010-09-15 22:35:24 |
 ez matek: Van 10 rabló, akik egy végtelen sok lakattal lezárható kincsesládát akarnak lelakatolni úgy, hogy semelyik 3 ne tudja kinyitni, de bármely 4 igen. Legalább hány lakat kell ehhez, ha egy rabló több kulcsot is kaphat? Légyszi segítsetek!!!
|
 |
|
| [1322] Janosov Milán | 2010-09-14 18:01:04 |
 üdv, az elektronikus munkafüzetbe nem tudok bejelentkezni - azért, mert tavaly végeztem? ez esetben, a régebben texben beküldött megoldásaimat sem tudom már megnézni (törölve lettek)?
|
|
| [1321] SmallPotato | 2010-09-13 17:34:18 |
 A "súrlódási energia" számomra nem tűnik igazán kezelhető fogalomnak.
Ha jól értem, a gond ott van, hogy igazából a kerületi erő állandóságára lenne szükség, ami - a csökkenő sugár miatt - csökkenő fékezőnyomatékot igényelne. Ezt képletszerűen elég macerás lenne felírni, bár időben egyenletes sugárcsökkenéssel tán nem lőnénk nagyon mellé. A fő gond inkább az, hogy hogyan állítasz elő időben változó fékezőnyomatékot.
A pneumatikus féked tápnyomását kellene (tudni) változtatni a huzalerő függvényében. Amennyire tudom, ezt nagyban úgy oldják meg, hogy a huzal egy görgőn van eltérítve, a görgő pedig egy nyomásszabályzó szelep karjának végén van (vagyis épp a huzalerő szabályozza a tápnyomást).
|
| Előzmény: [1320] Abi8211, 2010-09-13 11:33:47 |
|
| [1320] Abi8211 | 2010-09-13 11:33:47 |
 Sziasztok!
Egy első ránézésre nagyon egyszerű kis problémával találom magam szemben. Van 1 forgó dobom, amiről folyamatosan tekercselem le a rá feltekercselt huzalt, megközelítőleg állandó sebességgel. Mivel a folyamatos letekercselés során csökken az átmérője a dobnak, és a tömege is, így a tehetetlenségi energiája folyamatosan csökken. A kérdésem az, hogy hogyan tudnám ezt legideálisabban fékezni, hogyan tudom meghatározni a súrlódási energiát ennek a rendszernek. Most jelenleg levegő működtetésű tárcsafék fékezi a rendszert, állandó nyomással, de letekercselés végén megnyújtja a huzalt, a túlzott fékhatás miatt szerintem. Segítségeteket előre is köszönöm! üdv:Robi
|
|
|
| [1318] bily71 | 2010-09-12 19:36:38 |
 Nézzük a jobboldalt tagonként:
a5=a1q4
a6=a1q5=a2q4
a7=a1q6=a2q5=a3q4
(itt azt használtuk fel, hogy an=amqn-m )
behelyettesítés után:
a5+a6+a7=a1q4+a2q4+a3q4
ebből a q4 tényezőt kiemelve kapjuk, hogy:
a5+a6+a7=q4(a1+a2+a3)
és innen már tudni fogod.
|
| Előzmény: [1317] gerpet, 2010-09-12 19:05:19 |
|
| [1317] gerpet | 2010-09-12 19:05:19 |
 Sziasztok! Lenne egy feladat, aminek a megoldását nem értem. Előre is elnézést kérek a rutinosabbaktól, hogy ilyen "egyszerű" (a feladatgyűjteményben, mint könnyű feladat szerepel) feladattal zargatlak benneteket. A feladat: "Egy mértani sorozat első hét tagjából az első három elem összege 26, a három utolsó elem összege pedig 2106. Mennyi a hét tag összege?" Az lenne a kérdésem, hogy az alábbi megoldásban az első egyenlőség hogyan jön ki?:
|
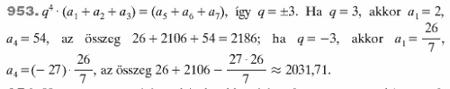 |
|
|
|
|
|
|
| [1311] bily71 | 2010-08-24 22:27:27 |
 Igazad van, de egy ilyen ellenpélda magyarázat nélkül összezavarhatja a diákokat, mondd el azt is, hogy miért!
A lényeg: az a1>0 és d>0 feltétel hiányzik.
Az ellenpéldádban a differencia d=0.
|
| Előzmény: [1310] Róbert Gida, 2010-08-24 20:03:19 |
|
|







 Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c
Q*, 0<a<b, vagyis irrac. számok! Ekkor létezik c, c soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta.
soronkövetkező tizedesjegyét irja, függetlenül attól, hogy J éppen melyik számot irta.






 t
t