| [1613] Jhony | 2012-01-09 17:30:46 |
 - megtudná-e mondani valaki mi a helyzet manapság ,ha valakinek van egy vagy kettő matematikai sejtése - már csak az a kérdés,hogy máig senki által nem említett sejtések-e és ...,hogy a matematika ,,világában" mennyire számítanak ,számítanának ,,érdekes",mondjuk ,,hasznos" sejtésnek - bizonyos szemszögből nézve ...
- a válaszokat,hozzászólásokat előre is köszönöm !
|
|
|
| [1611] bloghus | 2012-01-09 13:07:50 |
 Egy cég kétféle terméket gyárt. A P(x; y) -3x(négyzet)-y(köb)+6xy profitot (millió forint) fejezi ki a termékek árainak függvényében (ezer forint). A termékek milyen egységára mellett maximális a profit és mennyi az értéke?
|
|
|
|
| [1608] Jhony | 2012-01-05 14:53:52 |
 - meg tudná mondani valaki hol van a hiba az alábbi bizonyításban --- ,ha van ??? --- és,hogy azt bizonyítja e helyesen amit gondoltam ,vagyis azt a bizonyos ,,sejtést" ?
1. subst. - let p and k , two prime numbers greater or equal 2,from the set of prime numbers, P, in the form : p=2a + 1 and k=2b + 1 , such that a and b are natural numbers,from the set of natural numbers N, - let m=2n ,m greater or equal 4,even number,from the set of natural numbers N and n grater or equal 2,natural number from set of natural numbers N, 2. concl. - every even integer greater than 2 can be expressed as the sum of two primes 3. prove:- by ,,reductio ad absurdum” * - step 0. for n=2 --- m=4 --- 4=2+2 ** - step 1. for - if n is greater or equal 3 so always will be a number a and b such that n=a + b + 1 - prove. 3=1+1+1 4=2+1+1 5=2 +2+1 ................ n=a+b+ 1 - so for n=k than k=a+b+1 - suppose that is true - for k+1=(a+b+1)+1=(k)+1=k+1 - so for k+1 is true - for n grater than 2 always will be a number a and b such that n =a+b+ 1 *** - step 2. - every even integer greater than 4 can be expressed as the sum of two primes m=p+k - prove by ,,reductio ad absurdum" - so than m is not equal p+k - so than 2n is not equal 2a+1+2b+1 - so than 2n is not equal 2a+2b+2 / divide both sides by 2 - so than n is not equal a+b+1 - so what is in contradiction with the proof from step 1. where n=a+b+1 was proved that is true - so than m=p+k is proved that is true so,, every even integer greater than 4 can be expressed as the sum of two primes” --- q.e.d.
- köszönöm szépen és bocsánat a zavarásért !
|
|
|
|
| [1605] logarlécész | 2012-01-02 17:44:53 |
 Ezek után mit csinálunk? Rendezzük, vagy azt mondjuk, hogy ha n tart a végtelenbe, akkor kb. n=n+1 => a=b => a kifejezés: 2/3a a tart a végtelenbe => 2/3a->0
A második attól függetlenül, hogy kihozza a jó megoldást(?), inkább fizikus megoldásnak tűnik a kerekítgetéssel. :-)
Az igazi megoldási menetben beírjuk a kifejezéseket és rendezgetjük tovább?
|
| Előzmény: [1601] lorantfy, 2011-12-30 16:48:24 |
|
|
| [1603] Kemény Legény | 2011-12-30 17:26:06 |
 Persze meg lehet oldani algebrai átalakítások nélkül is, geometriai úton. Rajzoljuk le egy négyzetrácsos lapra a téglalapot. Ekkor a területét a téglalapban lévő kis négyzetek száma adja, míg a kerületének mérőszáma = határon levő kis négyzetek + 4 (a sarkoknál 2-szer kell számolni, meg persze fel kell tenni, hogy a és b 1-nél nagyobbak), így ha a terület és kerület azonos, akkor a szigorúan belül levő (a határral nem érintkező) kis négyzetek száma pont 4 kell legyen, azaz 1*4-es vagy 2*2-es téglalapot alkotnak, azaz az eredeti téglalap 3*6-os vagy 4*4-es volt.
|
|
| [1602] HoA | 2011-12-30 17:17:52 |
 Igen, ez a szép megoldás, de "bambán" is megy. Fejezzük ki a-t ab=2a+2b-ből. 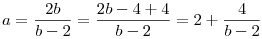 Innen már adódik, hogy (b-2) csak 4 osztói közül kerülhet ki. Innen már adódik, hogy (b-2) csak 4 osztói közül kerülhet ki.
|
| Előzmény: [1591] Alma, 2011-12-29 15:26:52 |
|
|
|
| [1599] Valvehead | 2011-12-30 07:42:01 |
 Egy jó félórát kínlódtam vele, hogy hogyan tudnám felhasználni a harmadik hatványra vonatkozó azonosságot harmadik gyökre, de nekem nem megy. Kaphatnék egy kis instrukciót?
|
| Előzmény: [1597] sakkmath, 2011-12-29 22:52:02 |
|
|
|
|
|
|
| [1593] Valvehead | 2011-12-29 19:02:08 |
 Ehhez a feladathoz kérnék szépen segítséget: http://imageshack.us/photo/my-images/832/1gyak2d.png/ Előre is köszönöm!
|
|
|
|
| [1590] Antal János Benjamin | 2011-12-29 14:31:08 |
 Elnézést, eléggé pontatlan vagyok. A feladat, hogy egy téglalap oldalai egész számok és területe és kerülete megegyezik, a két megoldás megvan, neten is kerestem rá megoldást, ott is csak a két megoldást láttam, konkrét levezetést sehol nem találtam. Tehát a és b is egész számok.
|
|
| [1589] takács krisztina | 2011-12-29 11:28:34 |
 Ha valai tud küldeni korábbi 9.-es Gordiusz feladatsorokat, annak nagyon örülnék, a takiri@freemail.hu címre kérem.
|
|
|
|
| [1586] Antal János Benjamin | 2011-12-29 02:16:29 |
 Sziasztok! Az alábbi egyenlőséget kéne megoldani (elvileg középiskolai emelt szintű matek tudással meg lehet ):
ab=2a+2b
Előre is köszönöm
|
|
|
|
| [1583] Lapis Máté Sámuel | 2011-12-10 15:51:11 |
 Sziasztok! Tudna valaki segíteni ebben a feladatban? A megoldás menetre is szükségem lenne!Mivel egyenlő 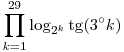 ? ?
|
|
|
| [1581] lorantfy | 2011-11-27 16:29:05 |
 Két pontból még nem tudod felírni a második parabola egyenletét. Kell még valamilyen információ. Jó lett volna, ha beírod az eredeti feladatot! Én arra gondolok, hogy a másik parabola szimmetria tengelye is az y tengely. Ha ez benne van az eredeti szövegben akkor BINGO! (Tudod honnan származik a BINGO szó?) Akkor csak egyetlen paramétert kell meghatározni, a-t. Mindkettőt toljad feljebb 10-el aztán integráljad őket -1-től +1 és a két integrál különbsége a közbezárt terület.
|
| Előzmény: [1580] laci777, 2011-11-27 15:56:42 |
|
| [1580] laci777 | 2011-11-27 15:56:42 |
 sziasztok!
tudna valaki segíteni az alábbi feladatban? meg kell(ene) határozni az y=3xnégyzet parabola, valamint az ezt az (1;3) pontban, az y tengelyt pedig a (0;-10) pontbam metsző másik parabola által bezárt terület nagyságát.
sajnos még a második parabolánál is annyit "sikerült" kiszámolnom, hogy (a+b)=13 (ahol az axnégyzet+bx-10 a második parabola egyenlete) onnan talán már menne(?)
előre is köszönöm szépen üdv laci
|
|
|
| [1578] Fálesz Mihály | 2011-11-22 06:55:05 |
 A különböző értelmben vett határértékeket nem lehet csak úgy össze-vissza cserélgetni (pedig időnként nagyon praktikus lenne). Itt legalább háromféle határérték keveredik össze, a végtelen szorzat, az egyes prímek kitevőinek összege, a különböző prímhatványok szintén végtelen szorzata... Tulajdonképpen végtelen sok divergens sorozat szorzatára próbálsz következtetni.
Ha a végtelen szorzat értéke egy pozitív racionális szám, akkor sem igaz, hogy egy prím kitevője a szorzatban (a részletszorzatok határértékében) egyenlő a tényezőkben szereplő kitevők összegével (a kitevők részletösszegei határértékével). Még akkor sem, ha a kitevők összege létezik.
Pl. lehet az összes ai tényező 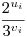 alakú, ahol ui,vi alkalmas pozitív egészek; ilyenek végtelen sorzataként minden nemnegatív szám előáll. (A alakú, ahol ui,vi alkalmas pozitív egészek; ilyenek végtelen sorzataként minden nemnegatív szám előáll. (A 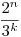 alakú számok a pozitív valós számok között sűrűn vannak.) alakú számok a pozitív valós számok között sűrűn vannak.)
De olyan végtelen szorzatot sem nehéz konstruálni, ahol az összes prím összesen kétszer szerepel, egyszer a számlálóban, egyszer a nevezőben, összességében minden prím ,,kiesik'', a szorzat értéke mégsem 1, hanem mondjuk 2.
|
| Előzmény: [1576] bily71, 2011-11-21 22:28:11 |
|
|
| [1576] bily71 | 2011-11-21 22:28:11 |
 Üdv!
Lenne egy kérdésem.
A pozitív racionális számok definíció szerint felírhatók két azonos előjelű egész hányadosaként. Az egyértelműség kedvéért vegyük csak azt az esetet, mikor mind a számláló, mind a nevező pozitív egész.
A számelmélet alaptétele szerint bármely egynél nagyobb pozitív egész, a sorrendtől eltekintve, egyértelműen bomlik prímszámok szorzatára. Ebből következik, hogy  n n N* felírható N* felírható 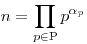 alakban, ahol P={prímek}, alakban, ahol P={prímek},  p p N és 0, vagy véges sok esetben igaz, hogy N és 0, vagy véges sok esetben igaz, hogy  p p 0. 0.
A fentiekből következik, hogy  q q Q+ felírható Q+ felírható 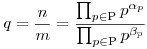 alakban, mely felírás egyértelmű, ahol n,m alakban, mely felírás egyértelmű, ahol n,m N*, (n,m)=1, N*, (n,m)=1,  p, p, p p N és 0, vagy véges sok esetben igaz, hogy N és 0, vagy véges sok esetben igaz, hogy  p, p, p p 0. 0.
Legyen (an,n N*) olyan sorozat, ahol ai N*) olyan sorozat, ahol ai Q+! Ekkor Q+! Ekkor 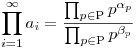 , mely alakot az egyszerűsítések elvégezte után kapunk. , mely alakot az egyszerűsítések elvégezte után kapunk.
A kérdésem:
Jól gondolom-e, hogy amennyiben az egyszerűsítések elvégezte után 0, vagy véges sok esetben igaz, hogy  p, p, p p 0, akkor 0, akkor 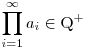 , különben , különben 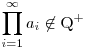 ? ?
Másik:
Jól gondolom-e, hogy ha létezik olyan prím, hogy a sorozat végtelen sok tagjára igaz, hogy a prím előfordul a nevezőben, de véges sok tagjára igaz, hogy előfordul a számlálóban, vagy fordítva, a sorozat végtelen sok tagjára igaz, hogy a prím előfordul a számlálóban, de véges sok tagjára igaz, hogy előfordul a nevezőben, akkor 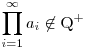 ? ?
|
|
|
| [1574] laci777 | 2011-10-17 15:45:56 |
 Sziasztok!
Ugyan most vesszük a deriválást, de egy feladat kifogott rajtam. Ha valaki tudna segíteni, megköszönném.
A példa: adott egy r sugarú gömb. Mekkora az ebbe a gömbbe szerkeszthető maximális térfogatú henger?
Bocs, ha túl egyszerű ez a pélfa, de bevallom kifog rajtam:(
Előre is köszönöm.
|
|
| [1573] Tóbi | 2011-10-15 18:16:03 |
 Legyen O egy pont a síkon. Legyen r az O távolságának maximuma az 5n adott objektumtól. Vegyünk egy O középpontú R sugarú kört. Ha R elég nagy, akkor belátjuk, hogy lesz rajta megfelelő P pont. A körvonal egy pontjának távolsága egy adott ponttól legalább R-r, ezen távolságok összege így legalább 2nR-2nr. Ha e egy adott egyenes, legyen e' a vele párhuzamos O-n átmenő egyenes. Ha p a körvonal egy pontja, akkor p és e távolsága legfeljebb annyi, mint p és e' távolsága plusz r. p és e' távolságának átlaga, miközben p fut a körön 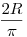 lesz, mivel ennyi a |sin(x)|R függvény átlagos nagysága is. Így összegezve a 3n egyenesre legfeljebb lesz, mivel ennyi a |sin(x)|R függvény átlagos nagysága is. Így összegezve a 3n egyenesre legfeljebb 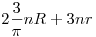 lesz az átlagos távolságösszeg. Ha R elég nagy, akkor lesz az átlagos távolságösszeg. Ha R elég nagy, akkor 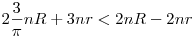 . Tehát valamely P pont jó lesz a körvonalon (például az, aminek minimális a távolságösszege az egyenesektől). . Tehát valamely P pont jó lesz a körvonalon (például az, aminek minimális a távolságösszege az egyenesektől).
|
| Előzmény: [1572] logarlécész, 2011-10-15 16:03:51 |
|
| [1572] logarlécész | 2011-10-15 16:03:51 |
 Adott a síkon 2n pont és 3n egyenes. Bizonyítsuk be, hogy van a síkon olyan P pont, hogy P-nek a 3n egyenestől való távolságainak összege kisebb, mint p-nek a 2n ponttól való távolságainak összege!
Eddig még n=1-re sem tudtam belátni.
Ha valaki tudna segíteni megköszönném. (Nem fontos és sürgős, csak érdekel.)
|
|
|
|
| [1569] phoenix | 2011-10-05 17:45:17 |
 Valamit én is gondoltam, de azt hittem átlátom amit írtam, de mégse ... lényegében az a) ill. b) feladatrész ugyanolyan elven működik ezek szerint, csak máshogy kell csoportosítani. Köszi a pontosítást vagy az érthetőbb megvilágítást :-) Köszi
|
| Előzmény: [1568] Sirpi, 2011-10-05 17:13:38 |
|
| [1568] Sirpi | 2011-10-05 17:13:38 |
 Uhh, belekavarodtam a skatulyáidba :-)
A lényeg, hogy 129 skatulyánk van (a prímek 129-es maradéka alapján), tehát valamelyik maradékból végtelen sok van, és erre a végtelen sok prímre igaz, hogy bármely kettő különbsége osztható 129-cel. Nyilván ez a bizonyítás tökéletesen működik bármilyen más számra is. Lényegében ezt írtad le Te is, csak túl sok volt a kérdőjel, és túl hosszúak a mondatok :-)
|
| Előzmény: [1567] phoenix, 2011-10-05 16:40:36 |
|
| [1567] phoenix | 2011-10-05 16:40:36 |
 Lemaradt a kérdőjel a végéről, de értelmesnek tűnhet? és ha azt kell bebizonyítani hogy végtelen sok prímszám van, melyek közül bármely kettőnek különbsége osztható 129-el? ügye itt is végtelen sok prímszámból válogatunk, de végtelen sokat abból is, mégpedig úgy hogy, mindegyik prímnek 129-el osztva ugyanolyan maradékot kell adnia. Erre is ugyanaz a skatulya-elv működhet? de az elsőnél véges sok skatulyába tettünk végtelen sok prímszámot, de itt véges skatulya van úgyszint, de nem csak egy elemre kell belátni, hanem hogy végtelen sok ilyen prímszámot tudunk kiválasztani, amik 129-el osztva azonos maradékot adnak.
|
|
| [1566] phoenix | 2011-10-05 16:32:45 |
 Az esetleg értelmesnek tűnhet, hogy tekintjük a 10 ad 10-en osztási maradékait, és ezeket tekintjük skatulyáknak, nyílván ezekből a skatulyákból véges sok van, ellenben azzal hogy végtelen sok prímszámunk van, és mindenképp lesz olyan két prímszám amit ha osztunk 10 ad 10-el, akkor ugyanannyi maradékot ad, és ezért különbségük osztható lesz vele.
|
| Előzmény: [1559] jonas, 2011-10-04 20:32:12 |
|
|
|





 3 , akkor van olyan a és b egész, hogy n=a + b + 1 , csak ezeket nem szabad összekeverni az elején definiált, k-hoz ill. p-hez tartozó a-val és b-vel.
3 , akkor van olyan a és b egész, hogy n=a + b + 1 , csak ezeket nem szabad összekeverni az elején definiált, k-hoz ill. p-hez tartozó a-val és b-vel.

 .
. 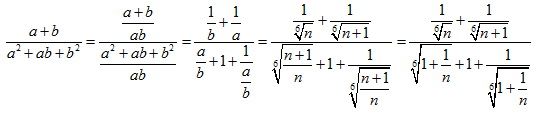


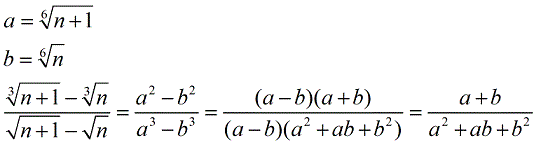




 Q+ esetén
Q+ esetén  p lehet végtelen is, sőt lehet, hogy nem is értelmezett. Előfordulhat, hogy
p lehet végtelen is, sőt lehet, hogy nem is értelmezett. Előfordulhat, hogy  n
n 0.
0.  p
p

