| [446] epsilon | 2008-04-11 10:56:21 |
 OK nadorp, kösz, valóban elszámoltam, mert Nekem a tg a 2n-en lett, mert egy sin a négyzeten "bennmaradt" :-( Túl csábító volt az a változócsere, és csodálkoztam is, hogy miért nem jön össze! Üdv: epsilon
|
| Előzmény: [440] nadorp, 2008-04-09 16:14:07 |
|
| [447] Sirpi | 2008-04-11 10:41:55 |
 Figyi, minden feladatod arra megy ki, hogy n-et két szám szorzatára kell bontani, és ahogy már írtam korábban, az sokjegyű számokra nehéz. Itt is a felbontás a lényeg, hiszen odáig az átalakítások teljesen triviálisak:
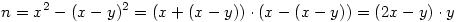
És ha most n páratlan (amit fel lehet tenni, mert ha páros, akkor osztjuk 2-vel, és n/2-et próbáljuk felbontani), akkor annak minden kéttényezős felbontására egyértelműen fogunk kapni egy páratlan y-t és egy egész x-et (n-nek minden y osztójához x=(y+n/y)/2).
Egyébként ennek könnyű megadni egy triviális megoldását, ha n páratlan (helyettesítsd be): x=(n+1)/2, y=1
Amúgy honnan szeded ezeket a felbontásokat?
|
| Előzmény: [445] csewe, 2008-04-11 10:03:14 |
|
| [445] csewe | 2008-04-11 10:03:14 |
 sziasztok
ismét kérnék egy levezetést
n = x négyzet - (x - y) a négyzeten
1 < y < n-1 valószínűleg páratlan
0 <= x pozitív egész
x -et és y -ont keresem
köszi
|
|
| [444] Róbert Gida | 2008-04-10 22:55:10 |
 Érdekes kérdés. Jelölje f(n) az osztók maximális számát (k n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre: n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre:
f(1)=1,f(2)=1,f(3)=2,f(4)=3,f(5)=4,f(6)=5,f(7)=5,f(8)=6,f(9)=7,f(10)=7,f(11)=7
Nagyobb n-re már nincs elég memóriája a gépemnek. Egyszerű program O(n!) memóriát igényel.
Hasonlóan az eredeti feladat bizonyításához így minden n 11-re f(n) 11-re f(n) n-4 is teljesül! Sőt szerintem nehéz számelméleti sejtésekkel rögzített c>0-ra f(n)<c*n is teljesül, ha n elég nagy. n-4 is teljesül! Sőt szerintem nehéz számelméleti sejtésekkel rögzített c>0-ra f(n)<c*n is teljesül, ha n elég nagy.
|
| Előzmény: [442] S.Ákos, 2008-04-09 21:37:21 |
|
|
| [442] S.Ákos | 2008-04-09 21:37:21 |
 Sziasztok!
A B.4055-ös feladatnál (Bizonyítsuk be, hogy minden n!-nál nem nagyobb pozitív egész szám felírható az n! legfeljebb n darab különböző osztójának összegeként.) egész könnyen adódik, hogy n-1 tag is elég n>1 esetén. a kérdés az lenne, hogy ennyi mindig kell-e, vagy ez is csökkenthető tovább, ha n nő, és ha igen, melyik az a függvény, ami megadja a tagok minimális számát?
|
|
| [441] Gyöngyő | 2008-04-09 18:16:40 |
 Sziasztok!
Lenne egy olyan kérdésem,hogy milyen esetben lehet parciális integrálást alkalmazni impropius integrál kiszámitására?
Köszike:
Zsolt
|
|
|
| [438] epsilon | 2008-04-09 15:48:31 |
 Köszi nadorp, mindjárt nem is merek szólni, mert ez valóban átvert, és nem is modhatni kemény diónak, én az x=a×cos2t változócsrét alkalmaztam, és tangenshatványnak az integrálja lett, amit csak rekurziósan bonyolítottam :-(
|
|
|
| [436] epsilon | 2008-04-09 14:25:40 |
 A 434. hsz-ban mindenütt (0,1) helyett [0,1] a helyes. Bocs az elírásért!
|
|
| [435] epsilon | 2008-04-09 14:08:01 |
 Annak örömére, hogy nadorp ilyen szép elemi megoldást adott, fe merészkedek tenni még egy feladatot, szimpatikus, de nem ugrik be :-( Igazolandó, hogy:
|
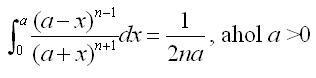 |
|
| [434] epsilon | 2008-04-09 11:01:28 |
 Köszi nadorp! Ez az igazi, amit nem találtam meg. Már-már részletezni akartam, hogy végre elég hosszadalmasan, de megoldottam, de nem tetszik, mert hosszú, noga ötletes. De azért elmesélem: patametrizáltam a [-1,-1/3] intervallumot, ennek parametrizált alakja (2/3)*t-1 ahol t a (0,1) intervallumban van. Tehát f(x) nem egyenlű ezzel az értékkel egyetlen t a (0,1) esetén sem. Ez azt jelenti, hogy a kapott x-ben másodfokú egyenletnek nincsenek valós gyökei, tehát a d<0 (d a diszkrimináns). Ekkor t-ben egy máodfokú egyenlőtlenséget kaptam, nullára rendeztem, és az kell teljesüljön minden t a (0,1) intertvallumból. A baloldali függfényt g(t)-nek jelölve, tehát g(t)<0 minden t a (0,1) intertvallumból. Végül a főegyüttható előjele szerint letárgyalvam mindkét esetben benne kell legyen a g(0)<0 és g(1)<0 feltétel, és a többiekkel is metszve marad ez, ami nem más mint a<-1/4. Kösz szépen mindegyikötöknek az ötletet és a segítséget! Üdv: epsilon
|
| Előzmény: [433] nadorp, 2008-04-09 08:51:32 |
|
| [433] nadorp | 2008-04-09 08:51:32 |
 Az, hogy f(x)<-1 vagy 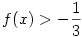 teljesül minden x-re ekvivalens azzal, hogy teljesül minden x-re ekvivalens azzal, hogy  teljesüljön minden x-re. teljesüljön minden x-re.
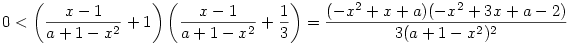
(x2-x-a)(x2-3x-a+2)>0
A baloldal egy pozitív főegyütthatójú negyedfokú polinom,ami pontosan akkor pozitív minden x-re, ha nincs valós gyöke, azaz a szorzatban szereplő másodfokú polinomok diszkriminánsa negatív. Innen 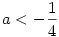
|
| Előzmény: [423] epsilon, 2008-04-07 19:41:32 |
|
| [432] Káli gúla | 2008-04-08 19:27:42 |
 A tört reciproka egyszerűbb függvény, a képe egy hiperbola lesz az y = -x-1 és az x=1 aszimptotákkal. Ha a>0, akkor a tompaszögű tartományban van a függvény és semmilyen értéket nem hagy ki. Ha a<0, akkor az y=-2 egyenesre szimmetrikus sávon kívül halad. Annak, hogy ez a reciprok függvény egy adott k értéket ne vegyen fel, az a feltétele, hogy az 1-x2+a=k(x-1) egyenletnek ne legyen megoldása, azaz a diszkrimináns d=k2+4(k+1+a)=(k+2)2+4a<0 legyen, tehát 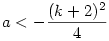 . Ez akár a -1-gyel, akár a -3-mal pont azt adja, amit cauchy írt. Ahogy a-val tartunk a 0-hoz, úgy fog a hiperbola "hegyesedni", és ezért belemetszeni az y=-1 és y=-3 közötti sávba. (A hiperbolára azért érdemes nézni, hogy elhiggyük azt, amit számolunk:) . Ez akár a -1-gyel, akár a -3-mal pont azt adja, amit cauchy írt. Ahogy a-val tartunk a 0-hoz, úgy fog a hiperbola "hegyesedni", és ezért belemetszeni az y=-1 és y=-3 közötti sávba. (A hiperbolára azért érdemes nézni, hogy elhiggyük azt, amit számolunk:)
|
| Előzmény: [431] epsilon, 2008-04-08 17:51:29 |
|
| [431] epsilon | 2008-04-08 17:51:29 |
 Helló! Én úgy próbáltam, hogy ne vegyen fel értékeket a [-1;-1/3] intervallumból, akkor f(x)<-1 vagy f(x)>-1/3 minden x valós szám esetén, aztán egy-egy törtet kaptam, amelyek másodfokú függvényeket tartalmaznak, ás próbáltam a diszkrimináns < 0 feltételeket, a baloldaliból jött ki eredmény, a jobboldaliból nem, de sejtem is a hibát: az f(x)<-1 nem muszáj MINDEN x-re fennáljon, amikor pl. ez nem áll fenn, azon x-re álljon fenn az f(x)>-1/3...tehát nem tudom, hogy a d<0 feltétellel egyáltalán lehetne-e valamit kezdeni. Nézem, a függvány monotonítását, onnan semmi, egyenlővé tettem y-nal és x-ben másodfokú egyenletnek valós megoldásai kell legyene, kaptam y-ra egyenlőtlenséget, vagyis képhalmazt...de ezt sem tudtam összhangba hozni az adott intervallummal..pedig a feladat nem tűnik komolynak, és mégis?!
|
| Előzmény: [430] cauchy, 2008-04-08 15:51:53 |
|
|
|
| [428] epsilon | 2008-04-08 09:10:51 |
 OK Cauchy, ez az eredmény, de Nekem csak az a<0 jön ki, valamit elveszítek :-( Ha a sejtésd bizonyítható, írhatnál egy pár támpontot! Előre is kösz, üdv: epsilon
|
| Előzmény: [424] cauchy, 2008-04-07 21:27:29 |
|
|
| [426] jonas | 2008-04-07 22:55:41 |
 Logaritmust a Taylor-sorral kell számolni, de úgy, hogy előbb leviszed a számot 1 közelébe (lehet fölötte vagy alatta) a log(xy)=logx.logy azonossággal, ahol y-nak ismered a logaritmusát. Ez számítógépnek praktikus, de ha kézzel akarsz logartimust számolni, általában a táblázat egyszerűbb.
|
| Előzmény: [425] leni536, 2008-04-07 22:22:31 |
|
| [425] leni536 | 2008-04-07 22:22:31 |
 A gyökvonásra való módszer nagyon tetszik, már el is sajátítottam a "digit by digit"-et. Más függvényekre van módszer a Taylor-soron kívül? Raj lenne papíron logaritmust számolni. Amúgy ha egy fügvénynek könnyebben számoljuk az inverz függvényét és inverz függvényének a deriváltját, a függvény mindenhol konvex, vagy mindenhol konkáv, akkor az alábbi sorozat határértéke tart a függvényünk értékéhez az x0 helyen:
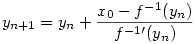
Ebből ki is jön n. gyökre a babilóniai módszer.
|
| Előzmény: [411] Sirpi, 2008-04-04 14:19:18 |
|
|
| [423] epsilon | 2008-04-07 19:41:32 |
 Helló! Megint van egy kedves feladat, látszatra jámbor:
|
 |
|
|
| [421] Sirpi | 2008-04-07 18:38:22 |
 Nem megy máshogy. A kettő teljesen ekvivalens: ha mondasz k-t és l-et, én megmondom x-et és y-t, és fordítva.
Ha nagy számokat akarsz felbontani, akkor amire rákereshetsz, mert sokkal jobban működnek, minthogy  -ig megnézünk minden prímet, hogy osztja-e n-t: -ig megnézünk minden prímet, hogy osztja-e n-t:
Pollard  -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk. -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.
|
| Előzmény: [418] csewe, 2008-04-07 14:59:55 |
|
|
| [418] csewe | 2008-04-07 14:59:55 |
 tulajdonképpen amint látom nekem n - et fel kel lbontanom "fejben/papiron" két szám szorzatára.
akkor viszont nem igen jutottam elöbre , mert ez nagyob számoknál már gondot okozhat. nincs más megoldás?
mert n felbontása csak találgatással megy.
|
| Előzmény: [420] Sirpi, 2008-04-07 13:42:32 |
|
| [420] Sirpi | 2008-04-07 13:42:32 |
 Oké, hogy csak páratlanra kell, de pl. a 10-et vagy a 42-t írd fel ilyen szorzat alakban, nem fog menni. Ahogy írtam, a 4-gyel oszthatók mennek, a csak 2-vel, de 4-gyel nem oszthatóak pedig nem.
Páratlanra meg úgy megy, ahogy írtam: n-et felbontod k.l-re, és innen 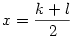 , ,  . .
Példa: n=91=7.13, ekkor 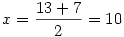 , , 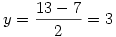 , és tényleg: 91=(10+3).(10-3) , és tényleg: 91=(10+3).(10-3)
|
| Előzmény: [417] csewe, 2008-04-07 12:50:16 |
|
| [417] csewe | 2008-04-07 12:50:16 |
 ismételten bocs
amire én használnám,ott
n mindíg páratlan pozitív egész
de nem értem miért nem lehet párosra felbontani hiszen
ha behejettesítem,akkor van olyan eset is
(6 + 2) * (6 - 2) = 32
de végül is ez mindegy mert nekem kimondottan páratlan
n - re kell a megoldás
a levezetést értem "azt hiszem", de még mindíg nem tudom
számszerüsíteni.
|
| Előzmény: [416] Sirpi, 2008-04-07 10:31:03 |
|
| [416] Sirpi | 2008-04-07 10:31:03 |
 Igazából az előző kérdésed után most nem vagyok egész biztos abban, hogy mire is vagy kíváncsi :-)
Ennek a feladatnak két része van, egy bazinehéz, meg egy könnyű. A bazinehéz az, hogy hogy bontsuk fel n-et két szám szorzatára (na jó, mondjuk tizensok jegytől tud ez már problémás lenni). Mivel x+y és x-y paritása azonos, ezért vagy mindkettő páros, vagy mindkettő páratlan. így n-et két azonos paritású szám szorzatára kell felbontani. Ha n páratlan, akkor nem is lehet máshogy, viszont ha n páros, akkor két páros szorzatára kell (egy 4k+2 alakú számot nem lehet így felbontani).
Ha ez megvan, vagyis n=k.l, ahol k l, akkor x+y=k, x-y=l, és innen triviálisan l, akkor x+y=k, x-y=l, és innen triviálisan 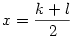 , ,  . .
|
| Előzmény: [415] csewe, 2008-04-07 05:35:20 |
|
| [415] csewe | 2008-04-07 05:35:20 |
 bocs de azt hiszem nem jól adtam meg az értéktartományt
x és y értéktartománya
2 < x , x pozitív egész
0 <= y < x - 2 , y pozitív egész
n pozitiv egész
talán így korrektebb
|
|
| [414] csewe | 2008-04-06 18:26:23 |
 heló mindenkinek
ismét segítséget kérnék
(x + y) * (x - y) = n
ha ezt valaki levezetné nekem nagyon megköszönném
n értékét mindíg ismerem x vagy y értékét kellene megállapítenom x és y értéktartománya 2 < x , 0 <= y
már egy napja lógok a neten hogy találjak valami mrgoldás,sőt előkotortam a régi matekkönyveimet is de semmire sem jutottam.
köszi
|
|
|
| [412] csewe | 2008-04-04 15:13:47 |
 mindenkinek kösz a segítséget a wikipédiás oldal angol,ugyhogy ez nálam kilőve
a gyökvonásból nemsokat értettem, mert éphogy hármas voltam matekból, és már az sem most volt
mivel ez az egyenlet amire itt megoldást kértem ,csupán a program gyorsítását szolgálta volna, így arra az elhatározásra jutottam, hogy más megoldást keresek
ti jók voltatok, csak ez már nekem magas
sziasztok
|
| Előzmény: [411] Sirpi, 2008-04-04 14:19:18 |
|
|
| [410] Róbert Gida | 2008-04-04 13:58:23 |
 Van egyébként osztásmentes verziója is a négyzetgyök kiszámolásának (ott szorozni kell). Továbbá a legjobb programok természetesen nem teljes pontossággal számolnak, mint te például 14 jeggyel, hanem mindig kb. megduplázzák az értékes jegyek számát az ak-ban.
|
| Előzmény: [409] Sirpi, 2008-04-04 12:42:14 |
|
| [409] Sirpi | 2008-04-04 12:42:14 |
 Ha már felmerült a téma, és azt állítottam, hogy a pontos jegyek száma iterációs lépésenként duplázódik, akkor kicsit pontosítanék, meg bizonyítanám is az állításomat. Tehát a rekurzió 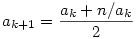
A számtani-mértani közepek közti egyenlőtlenség szerint ez mindig legalább 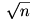 , így tegyük fel, hogy , így tegyük fel, hogy  (tehát x-nek c( (tehát x-nek c( 0) a hibája), és nézzük meg, hogy x-re alkalmazva az iterációt, mekkora lesz a következő tag, azaz 0) a hibája), és nézzük meg, hogy x-re alkalmazva az iterációt, mekkora lesz a következő tag, azaz 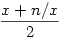 hibája. hibája.
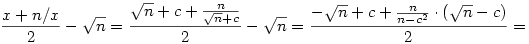
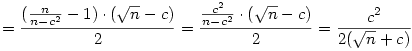
Ebből már pár dolog kiolvasható. Ha x nagy  -hez viszonyítva, akkor a hiba nagyjából feleződik: x=tn, ekkor c is hasonló nagyságrendű, és -hez viszonyítva, akkor a hiba nagyjából feleződik: x=tn, ekkor c is hasonló nagyságrendű, és 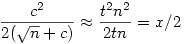
Viszont ha már c<1, akkor a következő hiba már kisebb, mint c2, vagyis valóban igaz a lépésenkénti duplázódó pontosság.
* * *
Ha gyorsítani akarunk az eljáráson, akkor annyit még érdemes megtenni, hogy a  -re adunk egy körülbelüli becslést, hogy az algoritmusnak ne kelljen az n,n/2,n/4... lépéseken végigmennie. Ha d alapú számrendszert használunk, akkor keressük meg a legkisebb k-t, amire n -re adunk egy körülbelüli becslést, hogy az algoritmusnak ne kelljen az n,n/2,n/4... lépéseken végigmennie. Ha d alapú számrendszert használunk, akkor keressük meg a legkisebb k-t, amire n d2k, és ilyenkor indítsuk az algoritmust dk-ból, ezzel az első jó pár lépést megspóroljuk. d2k, és ilyenkor indítsuk az algoritmust dk-ból, ezzel az első jó pár lépést megspóroljuk.
Egy példa a  kiszámolására, a1=2 indulóértékkel: kiszámolására, a1=2 indulóértékkel:
2,00000000000000 --- 1,50000000000000 --- 1,41666666666667 --- 1,41421568627451 --- 1,41421356237469 --- 1,41421356237309 --- 1,41421356237309
Vagyis a 6. érték már 14 jegyre pontos.
|
| Előzmény: [406] Sirpi, 2008-04-03 10:40:19 |
|
| [408] Hajba Károly | 2008-04-04 00:18:51 |
 Hallgass Sirpire, meglásd megéri!
Mivel a Sirpi javasolta rekurziós gyökvonás pontossága hatványozottan nő, így nagy számok esetén is gyors eredményt adhat. Talán nagyobb problémád lesz a nagy számok kezelésével, mint ezzel az eljárással.
|
| Előzmény: [407] csewe, 2008-04-03 14:48:10 |
|
| [407] csewe | 2008-04-03 14:48:10 |
 tulajdonképpen a szummát (remélem jól fogalmazok" szeretném visszafejteni n = (1 + 2 + 3 + 4 + ...végtelen) az egyenlettel megkapom ,hogy hányadik lépésnél éri el az n -et az összedás.
ehhez tudnotok kell hogy az eredeti képletem n = x * (x + 1 ) / 2 volt ezzel a képlettel megkaptam hogy hány számot kell összeadnom ,hony n -hez jussak.
reményeim szerint egy prímszitához tudom majd felhasználni a képletet , amivel néhányszáz esetleg néhányezer digites számokrol mondanám meg hogy prím e
a gyökvonás hosszú időtrabló folyamat, és nekem gyors algoritmus kellene
de sajnos nem ez az egyetlen probléma , hanem a nagy számok programozása is úgyhogy egyenlőre csak akkora számokra írom meg a rutint amekkorát a programnyelv alapból kezelni tud ,és ha sikeres akkor rátérek a nagyobb feladatra
ez nekem csak kedvtelés , de nagyon megköszönném, ha segitenétek.
|
| Előzmény: [406] Sirpi, 2008-04-03 10:40:19 |
|
| [406] Sirpi | 2008-04-03 10:40:19 |
 Igazából mire és milyen környezetben kell Neked erre megoldást adni? Mert amit írtam (a másodfokú egyenlet megoldóképlete szerinti megoldást), az a megoldás, és más nincs, szóval nem lehet gyökjel nélkül felírni. Programmal akarod esetleg csinálni? (Mert ott elvileg van gyökvonás.) Meg milyen nagyságrendű az n? Ha ezekre választ adsz, akkor jobban segíteni tudunk talán abban, amire szükséged van.
* * *
A gyökvonást mi magunk is implementálhatjuk, alapműveletekkel, ha épp nem akarunk beépítettet használni. Legyen mondjuk a1=1 (vagy a 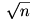 bármilyen közelítése, ha tudunk jobbat), majd bármilyen közelítése, ha tudunk jobbat), majd  . Ez a rekurzió nagyon gyorsan tart a . Ez a rekurzió nagyon gyorsan tart a 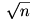 -hez, ak+1-nek kétszer annyi jegye pontos, mint ak-nak. Csak be kell állítani valami leállási paramétert, hogy a program ne fusson a végtelenségig (pl. -hez, ak+1-nek kétszer annyi jegye pontos, mint ak-nak. Csak be kell állítani valami leállási paramétert, hogy a program ne fusson a végtelenségig (pl. 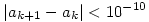 , vagy amilyen pontosság nekünk kell). , vagy amilyen pontosság nekünk kell).
|
| Előzmény: [405] csewe, 2008-04-03 08:42:26 |
|
|
|
| [403] csewe | 2008-04-02 17:50:26 |
 köszi a megoldást
még azt kérdezném,hogy nem menne ez gyökvonás nélkül
mert nagy számoknál ez elég problémás
|
|
|
| [400] csewe | 2008-04-02 17:02:09 |
 sziasztok
meg kellene oldanom ezt az egyenletet
n = x*(x + 1)
n pozitív egész pl:30 , 42 , 50 stb
szeretném megkapni x - et
persze nem ezeknél a kis számoknál okoz gondot a dolog
ha valaki tudja legyenszives vezesse le nekem a megoldást
köszi
|
|
|
| [398] Sirpi | 2008-03-26 16:31:32 |
 A 3.-at annyival egészíteném én ki, hogy mivel a 45 és a 102 lnko-ja 3, ezért azzal rögtön le lehet osztani:
34x+15y=53/3
Vagyis nincs egész megoldás, mert a bal oldal biztos egész, a jobb meg nem.
|
| Előzmény: [396] BohnerGéza, 2008-03-26 10:32:40 |
|
|
|





 n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre:
n!-ig minden egész előáll n!-nak legfeljebb f(n) darab különböző (pozitív) osztójának összegeként). Dinamikus programozással kiszámítható ez a sorozat kis n-ekre:  11-re f(n)
11-re f(n)


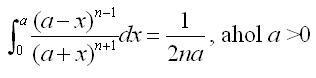





 -módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.
-módszere és Pollard p-1-módszere, vagy a kvadratikus szita. Mondjuk egyiket se lehet 10 sorban leprogramozni, szóval így állj hozzájuk.

