English Issue, December 2002
	Previous page	Contents	Next page	ORDER FORM

Solutions to the problems of the Kürschák Competition, 2001

Gyula Károlyi

1. Given 3n-1 points in the plane, no three of which are collinear, show that it is possible to select 2n points, such that their convex hull should not be a triangle.

Solution 1. The claim is obvious if n=1. For n>1, we have to prove that there exist 2n among the given points, such that their convex hull has at least 4 vertices. If we manage to find m\(\displaystyle \ge\)2n points whose convex hull has at least 4 vertices, then m-2n of them can be deleted so that the convex hull of the remaining points should still have at least 4 vertices.

Thus if the convex hull of the set \(\displaystyle \mathcal{P}\) of the points is not a triangle then we are done. Therefore we can assume that the convex hull of \(\displaystyle \mathcal{P}\) is a triangle A₁B₁C₁. Assume that for some i<n, we have already defined the points A₁,..., A_i, such that for all j\(\displaystyle \le\)i the convex hull of the set \(\displaystyle \mathcal{P}\setminus\{A_1,\dots,A_{j-1}\}\) is the triangle A_jB₁C₁. The set \(\displaystyle \mathcal{P}\setminus\{A_1,\dots,A_{i}\}\) has at least 2n elements, thus by the previous argument we can assume that the convex hull of that set is also a triangle. Two vertices of that triangle are clearly B₁ and C₁. Let A_i+1 denote the third vertex.

Thus we have shown that if it is not possible to select 2n points whose convex hull is not a triangle, then there exists a sequence A₁,A₂,...,A_n of points in \(\displaystyle \mathcal{P}\), such that for all i\(\displaystyle \le\)n, the convex hull of \(\displaystyle \mathcal{P}\setminus\{A_1,\dots,A_{i-1}\}\) is the triangle A_i B₁C₁. The point sequences B₁,B₂,...,B_n and C₁,C₂,...,C_n can be constructed in the same way. Among the 3n points hence obtained, there must be two points that coincide. Without the loss of generality we can assume that A_j=B_k. Then the set

\(\displaystyle \mathcal{P}\setminus\{A_1,A_2,\dots,A_n\}\setminus\{B_1,B_2,\dots,B_n\}\setminus\{C_1\} \)

has at least n-1\(\displaystyle \ge\)1 elements, all of which are interior points of both triangles A_jB₁C₁ and B_kA₁C₁. But that is impossible, as the two triangles have no common interior points. This contradiction proves the claim.

Remarks. 1. It is not hard to show that the number of points in the problem cannot be decreased to 3n-2: Let A₁B₁C₁ be an equilateral triangle with centre O, and let A, B, C be the midpoints of OA₁, OB₁, OC₁, respectively. Let k_A, k_B, k_C be circular arcs of radius R that connect A₁ and A, B₁ and B, C₁ and C, respectively. Finally, let the points A₂,..., A_n, B₂,...,B_n-1, C₂,...,C_n-1 lie on the arcs k_A, k_B, k_C. If n\(\displaystyle \ge\)2 and R is big enough then it is not possible to select 2n points of the (3n-2)-element set \(\displaystyle \mathcal{P}=\{A_1,\dots,A_n,B_1,\dots, B_{n-1},C_1,\dots,C_{n-1}\}\), such that their convex hull should not be a triangle. This is true because if R is big enough then each line A_iA_j separates the points B_k and \(\displaystyle C_\ell\). Thus if A_i and A_j are both vertices of the convex hull of a subset of \(\displaystyle \mathcal{P}\), then it may contain at most n-1 points other than A₁,...,A_n, and therefore the subset itself may contain at most 2n-1 points. Similar reasoning applies if the convex hull contains at least two of the points B_i or the points C_i as vertices. Therefore, the convex hull of every 2n-element subset may only contain one A_i, one B_i and one C_i as vertices, and that makes it necessarily a triangle.

2. For any real number x denote the smallest integer not smaller than x by \(\displaystyle \lceil x\rceil\). It can be shown that the claim can be improved as follows:

Let n\(\displaystyle \ne\)3. Given \(\displaystyle \lceil3n/2\rceil-1\) points in the plane, no three of which are collinear, it is possible to select n of them, such that their convex hull is not a triangle.

The two solutions below prove this stronger statement. Note that the condition makes sense for positive integer n only, and that for n\(\displaystyle \le\)2 the claim obviously holds. Thus, in what follows, n is greater than 3. If n is odd, then a minor adjustment of the previous counterexample shows that the claim fails to hold if the number of points is reduced to \(\displaystyle \lceil3n/2\rceil-2\).

Solution 2. Assume that \(\displaystyle \mathcal{P}\) is a set of at least \(\displaystyle \lceil3n/2 \rceil-1\) points that does not contain n points whose convex hull is not a triangle. Let the convex hull of \(\displaystyle \mathcal{P}\) be the triangle ABC, and let A₁=A. As in Solution 1, construct the sequence \(\displaystyle A_1,A_2,\dots,A_{\lceil n/2\rceil}\) such that for all \(\displaystyle i\le\lceil n/2\rceil\), the convex hull of \(\displaystyle \mathcal{P}\setminus\{A_1,\dots,A_{i-1}\}\) is the triangle A_iBC.

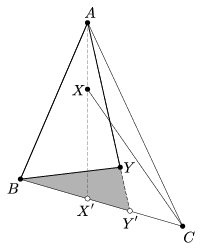
Consider the points \(\displaystyle A_2,\dots,A_{\lceil n/2\rceil}\) in counterclockwise order as seen from the point A. Let X and Y denote the first and last of them, respectively. Let X' and Y' be the intersections of lines AX and AY with the segment BC. We can assume, without loss of generality, that the order of points on the line BC is B, X', Y', C. One of the triangles BCX and BCY contains the other one. The smaller one of the two triangles, which is covered by the union of triangles BYY' and CXX', contains the set \(\displaystyle \mathcal{P}'=\mathcal{P} \setminus\big\{A_1,A_2,\dots,A_{\lceil n/2\rceil},B,C\big\}\). \(\displaystyle \mathcal{P}'\) has at least n-3 elements. We can clearly assume that at least half of these points lie inside the triangle BYY' (figure). Select \(\displaystyle \big\lceil(n-3)/2\big\rceil\) ones out of these points and denote this set by \(\displaystyle \mathcal{P}''\). Finally, let \(\displaystyle \mathcal{Q}=\mathcal{P}''\cup\big\{A_1,A_2,\dots,A_{\lceil n/2\rceil},B\big\}\). \(\displaystyle \mathcal{Q}\) has \(\displaystyle \big\lceil(n-3)/2\rceil+\lceil n/2\big\rceil+1=n\) elements, each of which lies either inside the triangle AY'B or on its boundary. Thus the points A, Y, B lie on the convex hull of Q. However, the convex hull of Q must also contain at least one point of the set \(\displaystyle \mathcal{P}''\), contradicting the assumption that \(\displaystyle \mathcal{P}\) does not contain n points whose convex hull is not a triangle.

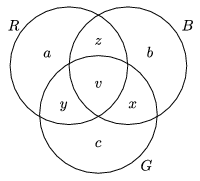
Solution 3 (by G. Lippner). As explained in Solution 1, we can assume that the convex hull of the points is a triangle ABC. Consider the points lying in the interior of this triangle ABC. Colour the segments connecting any two of the given points red, blue or green, depending on which side of the triangle they do not intersect: AB, BC, or CA, respectively. Let R, B, G, denote the sets of points incident to red, blue, green segments, respectively. Since n\(\displaystyle \ge\)4, there must be at least 2 points in the interior of triangle ABC, therefore the set R\(\displaystyle \cup\)B\(\displaystyle \cup\)G is the same as the set of points inside the triangle, and thus it has \(\displaystyle \lceil3n/2 \rceil-4\) elements. We show that one of the sets R, B, G must have at least n-2 elements.

Let us represent the sets on a Venn diagram. The letters denote the number of elements in the corresponding subsets.

If, say, a\(\displaystyle \ne\)0, then there is a point in the interior of the triangle that is connected to each of the other points with a red segment. Then

\(\displaystyle |P|=\lceil3n/2\rceil-4\ge n-2, \)

as n\(\displaystyle \ge\)4. Therefore, we can assume that a=b=c=0. Hence

|R\(\displaystyle \cup\)B\(\displaystyle \cup\)G|= x+y+z+v.

Now if each of

|R|=y+z+v, |B|=z+x+v and |G|=x+y+v

were smaller than n-2, then this would imply the inequality

\(\displaystyle 3n-8\le2\big(\lceil3n/2\rceil-4\big)=2(x+y+z+v)\le|R|+|B|+|G|\le3(n-3)=3n-9, \)

a contradiction.

Therefore, it is true that one of the sets has at least n-2 elements. Assume that |R|\(\displaystyle \ge\)n-2\(\displaystyle \ge\)2. Consider the set R'=R\(\displaystyle \cup\){A,B}. R' has at least n elements, and its convex hull contains the vertices A and B. Let D\(\displaystyle \in\)R, and let E be a point in R for which the segment DE is red. As the line DE does not intersect the segment AB, E cannot be in the interior of triangle ABD. Hence the convex hull of R' cannot be a triangle. Now it is clearly possible to select a subset of at least n\(\displaystyle \ge\)4 elements from R', such that their convex hull is not a triangle either.

2. Let k\(\displaystyle \ge\)3 be an integer, and \(\displaystyle \){k\choose3}">. Prove that if a_i, b_i, c_i (1\(\displaystyle \le\)i\(\displaystyle \le\)n) are 3n distinct real numbers then there are at least k+1 different numbers among the numbers a_i+b_i, a_i+c_i, b_i+c_i. Show that the statement is not necessarily true for \(\displaystyle n={k\choose3}\).

Solution 1. Assume that the statement is not true, that is, there are at most k different numbers among the sums a_i+b_i, a_i+c_i, b_i+c_i. Let T denote the set of these numbers. It is obvious that for every 1\(\displaystyle \le\)i\(\displaystyle \le\)n, the numbers a_i+b_i, a_i+c_i, b_i+c_i are pairwise different, and thus form a 3-element subset of T. Furthermore, if a_i+b_i=x, a_i+c_i=y, b_i+c_i=z then a_i=(x+y-z)/2, b_i=(x+z-y)/2, c_i=(y+z-x)/2, and thus, the set {x,y,z} uniquely determines the set {a_i,b_i,c_i}. As

\(\displaystyle {|T|\choose3}\le{k\choose3}

there exist indices 1\(\displaystyle \le\)i<j\(\displaystyle \le\)n, such that {a_i,b_i,c_i}= {a_j,b_j,c_j}, contradicting to the condition.

For the second part, consider the set T={t₁,t₂,..., t_k}, where t_i=4ⁱ. Let \(\displaystyle n={k\choose3}\), and let T₁,T₂,...,T_n denote the 3-element subsets of T. If T_i={4^u, 4^v,4^w}, where 1\(\displaystyle \le\)u<v<w\(\displaystyle \le\)k are integers, then let

a_i=(4^u+4^v-4^w)/2, b_i=(4^u+4^w-4^v)/2 and c_i=(4^v+4^w-4^u)/2.

Clearly a_i+b_i, a_i+c_i, b_i+c_i\(\displaystyle \in\)T. Hence it is enough to show that the numbers a_i, b_i, c_i (1\(\displaystyle \le\)i\(\displaystyle \le\)n) are all different.

a_i=b_j or a_i=c_j are not possible for any i,j, as the numbers a_i are all negative, whereas b_j and c_j are all positive. b_i=c_j is not possible either, as each b_i lies in some interval (2^2s-2, 2^2s-1), while each c_i lies in an interval of the form (2^2s-1, 2^2s) where 3\(\displaystyle \le\)s\(\displaystyle \le\)k is an integer.

Now let T_i={4^u, 4^v, 4^w} and T_j={4^x, 4^y, 4^z}, where 1\(\displaystyle \le\)u<v<w\(\displaystyle \le\)k and 1\(\displaystyle \le\)x<y<z\(\displaystyle \le\)k are integers. Suppose that c_i=c_j. Then

4^v+4^w-4^u= 4^y+4^z-4^x.

As 4^w<4^v+4^w-4^u<4^w+1, and 4^z<4^y+4^z-4^x<4^z+1, this can happen only if w=z, and thus 4^v-4^u=4^y-4^x. Here 4^v-1<4^v-4^u<4^v and 4^y-1<4^y-4^x<4^y, and therefore equality can hold only if v=y and then necessarily u=x and i=j. Thus the numbers c_i are all different. A similar reasoning shows that the numbers a_i and the numbers b_i are all different. That completes the proof.

Solution 2. This is a different proof for the first part of the problem, by D. Kiss. Assume again, to the contrary, that there are at most k different numbers among the 3n sums. Then there is a sum that occurs at least \(\displaystyle \frac{3n}{k\){k-1\choose2}"> times. Let a denote that sum. If two of the sums a_i+b_i, b_i+c_i and a_i+c_i were equal to a for some i, then there would be two equal numbers among a_i, b_i and c_i. Thus we can assume that for all \(\displaystyle 1\le i\le{k-1\choose2}+1\), exactly one of the sums a_i+b_i, b_i+c_i and a_i+c_i equals a. Now the remaining \(\displaystyle 2\left({k-1\choose2}+1\right)\) sums can assume only k-1 different values. Therefore, there is a value, some b, that occurs at least

\(\displaystyle 2\left({k-1\choose2}+1\right)\Big/(k-1\)k-2 ">

times. By the previous argument, we can assume that for all 1\(\displaystyle \le\)i\(\displaystyle \le\)k-1, one of the sums a_i+b_i, b_i+c_i, a_i+c_i is a and another one is b. The k-1 sums still remaining can only assume k-2 different values, and hence two of them are equal. But then the corresponding numbers a_i, b_i, c_i are also equal. This contradiction proves the statement.

In what follows there are further constructions for the second part of the problem.

Solution 3. Consider the set T={t₁,t₂,..., t_k}, where t_i=3ⁱ. Let {x,y,z} and {u,v,w} be two 3-element subsets of the set {1,2,..., k}. As in Solution 1, it is enough to show that if

\(\displaystyle \frac{3^x+3^y-3^z}{2}=\frac{3^u+3^v-3^w}{2}, \)

then the two subsets are necessarily equal, and z=w. It follows from the equality that

3^x+3^y+3^w=3^u+3^v+3^z=A.

If A is written in base-3 notation, then its non-zero digits contain either three 1's, or one 1 and one 2, as x=y=w is not possible. The base-3 notation of a number is unique, thus in the first case, {x,y,w} and {u,v,z} are the same 3-element subsets of the set {1,2,..., k}. Since x,y\(\displaystyle \ne\)z, this yields w=z and hence {x,y}={u,v}, indeed. In the second case we have that {x,y,w} and {u,v,z} are identical 2-element subsets of {1,2,...,k}. As x\(\displaystyle \ne\)y, this subset must be identical to the set {x,y} and this would imply z\(\displaystyle \in\){x,y} which is impossible.

Solution 4. As also suggested by the above solutions, it is enough to show that for every positive integer k, there exists a set T_k={t₁,t₂,..., t_k} for which t_x+t_y+t_z=t_u+t_v+t_w is true if and only if the numbers x, y, z are identical to the numbers u, v, w in some order. Then it is easy to show that the \(\displaystyle 3{k\choose3}\) numbers of the form (t_x+t_y-t_z)/2 (where {x,y,z} is an arbitrary 3-element subset of the set {1,2,..., k}) are all different.

If k=1, then t₁=1 is obviously a good choice. It is enough to show that there exists an infinite sequence t₁,t₂,...,t_i,..., such that for all i\(\displaystyle \ge\)2, t_i cannot be expressed in the form r₁t₁+^...+ r_i-1t_i-1, where r₁,..., r_i-1 are rational numbers. Indeed, assuming that such a sequence exists, consider the set T_k, and suppose that t_x+t_y+t_z=t_u+t_v+t_w for some 1\(\displaystyle \le\)x,y,z,u,v,w\(\displaystyle \le\)k. Let i be the greatest one of the indices x, y, z, u, v, w. Now if t_i does not occur the same number of times on both sides of the equality, then rearrangement yields an equality of the form t_i=r₁t₁+^...+r_i-1t_i-1. Thus i occurs the same numbers of times among x, y, z as among u, v, w. Cancelling the terms equal to t_i on both sides, and repeating the above procedure, one finally concludes that the numbers x, y, z indeed coincide with u, v, w in some order.

Assume, therefore, that k>1 and the numbers t₁,...,t_k-1 have already been determined according to the above requirement. Then the infinite set of numbers that can be expressed in the form r₁t₁+^...+ r_k-1t_k-1 is denumerable, while the set of all real numbers is not. Thus, there exists a real number t_k that cannot be expressed in the form r₁t₁+^...+ r_k-1t_k-1. Hence the existence of a sequence of the required property follows directly from the principle of mathematical induction.

Remark. 1. The last solution uses a non-constructive method to prove the existence of an appropriate sequence t₁,t₂,...,t_i,... . It can be shown that the choice \(\displaystyle t_i=\sqrt{p_i}\), for example, yields a suitable sequence. (p_i denotes the i-th positive prime number.) The proof, however, is beyond the scope of this article.

2. As observed by A. T. Kocsis, the problem can be generalized as follows. Let k\(\displaystyle \ge\)t\(\displaystyle \ge\)3 be integers and \(\displaystyle \){k\choose t}">. If a_i1,a_i2, ...,a_it (1\(\displaystyle \le\)i\(\displaystyle \le\)n) are tn different real numbers then there are at least k+1 different numbers among the sums \(\displaystyle \sum_{j=1}^ta_{ij}-a_{ik}\) (1\(\displaystyle \le\)i\(\displaystyle \le\)n, 1\(\displaystyle \le\)k\(\displaystyle \le\)t), but this is not necessarily so if \(\displaystyle n={k\choose t}\). The proof is left to the reader as an exercise as it does not require any new idea.

3. The story is entirely different if we ask about two term sums. It is clear that if k\(\displaystyle \ge\)3 is an integer, \(\displaystyle \){k\choose3}">, and a_i, b_i, c_i, d_i (1\(\displaystyle \le\)i\(\displaystyle \le\)n) are 4n different real numbers, then there are at least k+1 different numbers among the sums a_i+b_i, a_i+c_i, a_i+d_i, b_i+c_i, b_i+d_i, c_i+d_i. Surprisingly enough this cannot be improved significantly. You can think about the following problem: for every integer k\(\displaystyle \ge\)3, there exist \(\displaystyle 4{k\choose3}\) different real numbers a_i, b_i, c_i, d_i \(\displaystyle \left(1\le i\le{k\choose3}\right)\), such that there are at most 2k different numbers among the sums a_i+b_i, a_i+c_i, a_i+d_i, b_i+c_i, b_i+d_i, c_i+d_i.

3. In a square lattice, consider any triangle of minimum area that is similar to a given triangle. Prove that the centre of its circumscribed circle is not a lattice point.

Solution 1 (by B. Gerencsér). Consider a lattice triangle whose circumcentre is also a lattice point. We can assume, without loss of generality, that one vertex (A) is the origin. Let the coordinates of the other two vertices be B=(a,b) and C=(c,d), and let the circumcentre be O=(x,y).

From the equality of the segments OA and OB, the Pythagorean theorem yields x²+y²=(a-x)²+(b-y)². Hence a²+b² is even, and thus so are a+b and a-b. By a similar argument, c+d and c-d are also even numbers.

Consider now the lattice triangle A₁B₁C₁, where

A₁=A, \(\displaystyle B_1=\left(\frac{a+b}{2},\frac{a-b}{2}\right)\) and \(\displaystyle C_1=\left(\frac{c+d}{2},\frac{c-d}{2}\right)\).

In this triangle,

\(\displaystyle {A_1B_1}^2=\left(\frac{a+b}{2}\right)^2+\left( \frac{a-b}{2}\right)^2=\frac{a^2+b^2}{2}= \frac{{AB}^2}{2},\)

\(\displaystyle {A_1C_1}^2=\left(\frac{c+d}{2}\right)^2+\left( \frac{c-d}{2}\right)^2=\frac{c^2+d^2}{2}=\frac{{AC}^2}{2} \)

and

\(\displaystyle {B_1C_1}^2=\left(\frac{a+b-c-d}{2}\right)^2+ \left(\frac{a-b-c+d}{2}\right)^2= \frac{{(a-c)}^2+{(b-d)}^2}{2}=\frac{{BC}^2}{2}. \)

Hence the lengths of the sides of the triangle A₁B₁C₁ are \(\displaystyle \frac{1}{\sqrt{2}}\) times the corresponding sides of the triangle ABC, and thus we have found a lattice triangle similar to the triangle ABC, but of smaller area. This proves the statement.

Solution 2. Assume that the circumcentre O of a lattice triangle H is also a lattice point. Let (x,y) be the coordinates of one of the side vectors, and let (a,b) and (c,d) be the coordinates of the position vectors of the endpoints of that side. Then a, b, c, d, x, y are integers, and from the Pythagorean theorem,

x²+y²= (a-c)²+ (b-d)²=(a²+b²)+(c²+d²)-2(ac+bd).

As a²+b²=c²+d² (the square of the radius of the circumscribed circle), x²+y² and thus also (x+y)² is an even number. It follows that x+y and x-y are also even.

By rotating the vector (x,y) through an angle of 45^o about the origin in the positive direction, we get the vector \(\displaystyle \left(\frac{x-y}{\sqrt{2}},\frac{x+y}{\sqrt{2}}\right)\). An enlargement of scale factor \(\displaystyle \frac{1}{\sqrt{2}}\) yields the vector \(\displaystyle \left(\frac{x-y}{{2}},\frac{x+y}{{2}}\right)\) which is a vector of integer coordinates.

Thus we have shown that by a rotation through 45^o and an enlargement of scale factor \(\displaystyle \frac{1}{\sqrt{2}}\), H is mapped onto a similar but smaller triangle. This proves the statement.

Remark. The diagonals drawn from one vertex of a cyclic polygon divide the polygon into triangles. As all these triangles have a common circumcentre, the statement of the problem is also valid for any cyclic polygon not just a triangle.