 | English Issue, December 2002 | |||
| Previous page | Contents | Next page | ORDER FORM | |
Remarks to the Olympiad
Géza Kós
We investigate Problem 6 of the International Mathematical Olympiad of this year. This article presents two solutions.
The first one, like the solution of Problem 2, does not make use of any special idea, and does not require anything beyond high-school mathematics, but it starts with a surprising step that might look discouraging at the first sight.
The second solution requires much more mathematical background. It uses as extension of the set of integers, the theory of the so-called Eulerian integers. This is the price for revealing the most probable origin of the problem.
Problem 6. Let a, b, c, d be integers, such that a>b>c>d>0. Given that
| (6) | ac+bd= (b+d+a-c)(b+d-a+c), |
show that ab+cd is not a prime number.
By rearranging equation (6), we have
| (7) | a2-ac+c2=b2+bd+d2. |
Let us use this form from now on.
Solution 1: Substitute.
The proof is indirect. Assume that ab+cd=p, where p is a prime. We have the simultaneous equations
| (8) | a2-ac+c2= b2+bd+d2, ab+cd=p. |
The number of unknowns and equations can be reduced by expressing some appropriate expression out of one equation and substituting it into the other. In order to make calculations more convenient, let us consider everything modulo p.
According to the second equation, ab\(\displaystyle \equiv\)-cd (mod p). Multiply equation (7) by b2, and substitute -cd for ab:
c0 = b2(b2+bd+d2-a2+ac-c2)= b4+b3d+b2d2-(ab)2+ab.bc- b2c2 \(\displaystyle \equiv\)
\(\displaystyle \equiv\)b4+b3d+b2d2- (cd)2- cd.bc- b2c2=(b+c)(b-c)(b2+bd+d2) (mod p).
The resulting expression is a product of three factors, one of which is equal to the quantity in equation (7). It follows from the congruence that one of the three factors b+c, b-c and b2+bd+d2 is divisible by p, as we assumed that p was a prime. The numbers b+c and b-c are positive and less than ab+cd=p, and thus cannot be divisible by p. There remains the only possibility that b2+bd+d2 is divisible by p. As
0<b2+bd+d2< ab+ab+cd< 2(ab+cd)= 2p,
the number b2+bd+d2 can only be divisible by p if it equals p. Hence the simultaneous equations to solve are
| (9) | a2-ac+c2= b2+bd+d2= ab+cd=p. |
No it is easy to show the contradiction. Consider equation (9) modulo a (as a is the largest one of the unknowns). It follows that c(c-d)= ab+ac-a2 is divisible by a. But that is impossible, as a and c are relative primes (or otherwise ab+cd could not be a prime), and 0<c-d<a.
Solution 2: With a little help from Euler.
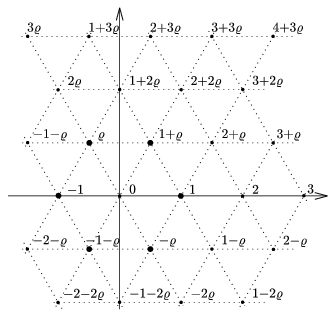
Figure 1
It is clear to anyone who has read about them that equation (7) is closely related to Eulerian integers.
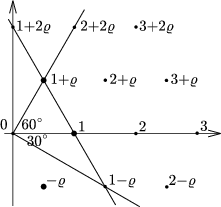
Let \(\displaystyle \varrho\) be a complex third root of unity. The complex numbers of the form x+y\(\displaystyle \varrho\), where x and y are integers, are called Eulerian integers. Eulerian integers form a lattice of regular triangles in the complex plane (Figure 1).
This number set has several remarkable and useful properties. Leonhard Euler also used these numbers when he proved Fermat's last theorem for the exponent 3. Let us briefly summarize the most important concepts and theorems related to Eulerian integers that will be needed in the proof.
Addition, subtraction and multiplication of Eulerian integers are defined in the natural way. Remember that \(\displaystyle \varrho\)2= -\(\displaystyle \varrho\)-1:
rcl(x+y\(\displaystyle \varrho\))\(\displaystyle \pm\)(u+v\(\displaystyle \varrho\)) & = & (x\(\displaystyle \pm\)u)+ (y\(\displaystyle \pm\)v)\(\displaystyle \varrho\);
(x+y\(\displaystyle \varrho\))(u+v\(\displaystyle \varrho\)) = xu+ (xv+yu)\(\displaystyle \varrho\)+ yv\(\displaystyle \varrho\)2 & = &(xu-yv)+ (xv+uy-yv)\(\displaystyle \varrho\).
The commutative, associative and distributive properties of addition and multiplication of integers or real numbers are also valid for Eulerian integers. The properties of the numbers 0 and 1 also remain valid: for example if 0 is added to any Eulerian integer, the sum equals the original number, or 0 times any Eulerian integer is 0.
The conjugate of an Eulerian integer \(\displaystyle \alpha\)=x+y\(\displaystyle \varrho\) is the number \(\displaystyle \overline{\alpha}=x+y\varrho^2=(x-y)-y\varrho\).
There is a very important quantity called the norm of an Eulerian integer. The norm of an Eulerian integer \(\displaystyle \alpha\)=x+y\(\displaystyle \varrho\) is denoted by N(\(\displaystyle \alpha\)) and defined as follows:
\(\displaystyle N(\alpha)=\alpha\cdot\overline{\alpha}=x^2-xy+y^2. \)
The norm is always a non-negative integer, and 0 is the only number whose norm is 0.
The norm is clearly equal to the square of the modulus of the complex number. Thus the norm of a product is the product of the norms of the factors:
N(\(\displaystyle \alpha\).\(\displaystyle \beta\))=N(\(\displaystyle \alpha\)).N(\(\displaystyle \beta\)).
An Eulerian integer \(\displaystyle \alpha\) is a factor of an Eulerian integer \(\displaystyle \beta\) if there exists an Eulerian integer \(\displaystyle \gamma\) such that \(\displaystyle \alpha\) =
= . It follows from the multiplicativity of the norm that if
. It follows from the multiplicativity of the norm that if  |
| then N(
then N( )|N(
)|N( ). (The latter divisibility is meant in the set of rational integers.)
). (The latter divisibility is meant in the set of rational integers.)
There are six Eulerian integers whose norm is 1. They are called units and marked in Figure 1. The units divide all Eulerian integers.
Two Eulerian integers are said to be associate if they are obtained from each other by multiplication with a unit, that is, by rotation about 0 through a multiple of 60o.
A non-unit Eulerian integer  is said to be irreducible if its only factors are the units and itself.
is said to be irreducible if its only factors are the units and itself.
A non-unit and non-zero Eulerian integer  is said to be a prime if
is said to be a prime if  |
|
 implies
implies  |
| or
or  |
| for any Eulerian integers
for any Eulerian integers  ,
,  . In order to distinguish the primes in the system of Eulerian integers from real primes, let us call them Eulerian primes.
. In order to distinguish the primes in the system of Eulerian integers from real primes, let us call them Eulerian primes.
The most important theorems of the theory of Eulerian integers are the following
[1.] Irreducible Eulerian integers are the same as Eulerian primes.
[2.] The fundamental theorem of number theory is valid for Eulerian integers, too: Every non-zero and non-unit Eulerian integer can be expressed as a product of Eulerian primes and units, and the representation is unique up to associates, that is, in any two representations, the corresponding factors are associates of each other.
[3.] The real primes of the form 3k+2 are also Eulerian primes. The primes of the form 3k+1 can be reduced to the product of two non-associate Eulerian primes (e.g. 7=(3+ )(2-
)(2- )). The prime factor decomposition of 3 is 3=-
)). The prime factor decomposition of 3 is 3=- 2(1-
2(1- )2.
)2.
The theorems show that there is a close relationship between the prime factors of an Eulerian integer  and the prime factors of N(
and the prime factors of N( ). The square of each prime factor 3k+2 of
). The square of each prime factor 3k+2 of  occurs in the prime factor decomposition of N(
occurs in the prime factor decomposition of N( ), and so do the norms of all the other prime factors, which are either 3 or primes of the form 3k+1.
), and so do the norms of all the other prime factors, which are either 3 or primes of the form 3k+1.
For example, let  =10+8
=10+8 . Its resolution into Eulerian primes is 2.(2+
. Its resolution into Eulerian primes is 2.(2+ )(3+
)(3+ ) and that of its norm is N(
) and that of its norm is N( )=N(2).N(2+
)=N(2).N(2+ ).N(3+
).N(3+ )=22.3.7.
)=22.3.7.
Conversely, the prime factors of N( ) ``almost determine" the prime factors of
) ``almost determine" the prime factors of  . All prime factors 3k+2 of N(
. All prime factors 3k+2 of N( ) are also prime factors of
) are also prime factors of  (with half the exponent), and each factor of 3 in the resolution of N(
(with half the exponent), and each factor of 3 in the resolution of N( ) is the norm of the Eulerian prime 1-
) is the norm of the Eulerian prime 1- . The prime factors 3k+1 of N(
. The prime factors 3k+1 of N( ) are also norms of prime factors of
) are also norms of prime factors of  , but there are two possible Eulerian primes in each case, even if associates are not considered different.
, but there are two possible Eulerian primes in each case, even if associates are not considered different.
Back to the problem: let  =a+c
=a+c and
and  =b-d
=b-d . According to the given condition, a2-ac+c2=b2+bd+d2, that is, N(
. According to the given condition, a2-ac+c2=b2+bd+d2, that is, N( )=N(
)=N( ). We have to prove that ab+cd, that is, the ``real part'' of
). We have to prove that ab+cd, that is, the ``real part'' of 
 =(ab+cd)+ (bc+cd-ad)
=(ab+cd)+ (bc+cd-ad) , cannot be a prime.
, cannot be a prime.
As N( )= N(
)= N( ), the prime factors of the two Eulerian integers are ``almost the same". They have some prime factors in common, and the remaining factors are pairwise conjugate. This can be put as follows:
), the prime factors of the two Eulerian integers are ``almost the same". They have some prime factors in common, and the remaining factors are pairwise conjugate. This can be put as follows:
| (10) | 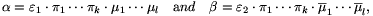 |
where  1,...,
1,..., k and
k and  1,...,
1,..., l are Eulerian primes and
l are Eulerian primes and  1,
1,  2 are units.
2 are units.
Let  =
= 1.....
1..... k and
k and  =
=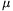 1.....
1.....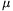 l as above. Then
l as above. Then
 =
= 1
1
 and
and 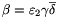 .
.
(It may happen that there are only common or only different prime factors in  and
and  ; then, of course
; then, of course  =1, or
=1, or  =1.)
=1.)
Consider now the number
| (11) |   = (ab+cd)+ (bc+cd-ad) = (ab+cd)+ (bc+cd-ad) = = 1 1  2 2  2.N( 2.N( ). ). |
This number is divisible by N( ), and thus ab+cd and bc+cd-ad are also divisible by N(
), and thus ab+cd and bc+cd-ad are also divisible by N( ). What remains to prove is that neither N(
). What remains to prove is that neither N( )=1 nor ab+cd=N(
)=1 nor ab+cd=N( ) is possible.
) is possible.
If N( )= 1, that is
)= 1, that is  =1, then
=1, then  and
and  are associates, which means that they can be obtained from each other by a few 60o rotations about 0. The number of these rotations is determined by the arguments of
are associates, which means that they can be obtained from each other by a few 60o rotations about 0. The number of these rotations is determined by the arguments of  and
and  .
.
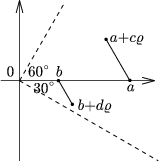
It follows from the condition a>b>c>d>0 that the argument of  is between 0o and 60o, and that of
is between 0o and 60o, and that of  is between -30o and 0o (Figure 2). Thus the difference of the arguments is between 0o and 90o, and hence the angle of rotation is exactly 60o, that is
is between -30o and 0o (Figure 2). Thus the difference of the arguments is between 0o and 90o, and hence the angle of rotation is exactly 60o, that is  =(1+
=(1+ )
) . But then,
. But then,
 = a+c
= a+c = (1+
= (1+ ) (b-d
) (b-d )= (b+d)+ b
)= (b+d)+ b ,
,
which is impossible, as b>c. Thus the assumption N( )=1 leads to a contradiction.
)=1 leads to a contradiction.
 |  |
| Figure 2 | Figure 3 |
If ab+cd=N( ), then by dividing equation (11) by N(
), then by dividing equation (11) by N( ) we get
) we get
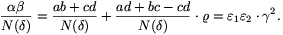
This number, as shown by the right-hand side, is an Eulerian integer. Its argument is the sum of the arguments of  and
and  , which is between -30o and 60o, and its ``real part'' is
, which is between -30o and 60o, and its ``real part'' is 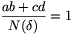 , by assumption. The only Eulerian integer satisfying this requirement is 1 (Figure 3), hence
, by assumption. The only Eulerian integer satisfying this requirement is 1 (Figure 3), hence  1
1  2
2 2=1 and
2=1 and 
 = N(
= N( ).
).
Thus the product of the numbers  and
and  is the positive real number N(
is the positive real number N( ). As N(
). As N( )=N(
)=N( ), it follows that the two numbers are conjugates. But then
), it follows that the two numbers are conjugates. But then
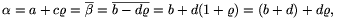
which is impossible, as c>d. The assumption ab+cd= N( ) also leads to a contradiction. This completes the proof.
) also leads to a contradiction. This completes the proof.
Solution 2 not only proves the statement of the problem, but also provides a construction for finding appropriate numbers a, b, c, d with a>b>c>d and
a2-ac+c2= b2+bd+d2.
All we need to do is find Eulerian integers of the appropriate arguments.
For example, setting
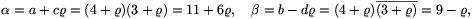
a=11, b=9, c=6 and d=1, with
a2-ac+c2= b2+bd+d2=91.
(Obviously, ab+cd=105 is not a prime.)
