New exercises and problems in Mathematics
November 1997
New exercises for practice in November 1997
C. 481. There is a company sitting at a round-table. They all leave the table for a while, and after returning to the table they all find that their neighbours differ from those they had previously. How many people may be sitting around the table?
C. 482. Prove that if y3x+1<x+y3 holds for some real numbers x and y, then they also satisfy inequality x3y+1<y+x3.
C. 483. The following question was presented at a Jeopardy show. Which plane figure has the property that its area is half the product of its diameters? According to te official answer, this is `the kite'. Are kites the only plane figures with the above property?
C. 484. In a right circular cone, the angle formed by the axis
and a generator measures 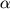 . Consider the
ball inscribed in the cone. Find the ratio of the volume of the ball and
that of the cone.
. Consider the
ball inscribed in the cone. Find the ratio of the volume of the ball and
that of the cone.
New exercieses in November 1997
Gy. 3158. The number 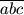 (as written in the decimal system) is divisible by 7. Prove that 7 can
be cancelled out of the fraction
(as written in the decimal system) is divisible by 7. Prove that 7 can
be cancelled out of the fraction  .
.
Gy. 3159. Find the smallest positive integer n for which
every real number x satisfies inequality
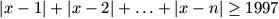 .
.
Gy. 3160. In an infinite arithmetic progression of distinct positive integers, we replace each term by the sum of its digits. Can it happen that the new sequence is again an arithmetic progression?
Gy. 3161. At a meeting there are n guest, including Mr. Smith. There is also a journalist there who is looking for Mr. Smith. He is aware of the fact that no one at the meeting knows Mr. Smith, who nevertheless knows everybody there. The journalist may approach any guest, point at someone, and ask the guest if s/he knows that specific person.
- a) Can the journalist find Mr. Smith for sure with less than n
questions?
- b) What is the minimum number of questions he has to ask before he can
identify Mr. Smith?
Gy. 3162. The lengths of the legs of a right triangle are a and b, respectively. Draw a circle of radius a centered at one endpoint of the hypotenuse, and also a circle of radius b centered at the other endpoint. Prove that the segment of the hypotenuse lying in the intersection of these two discs is as long as the diameter of the incircle of the triangle.
Gy. 3163. Find the minimum number of different lines determined by n non-collinear points in the plane.
Gy. 3164. In a triangle, let S, M, O and K denote respectively the centroid, the orthocentre, the incentre and the circumcentre of the triangle. Suppose that some two of these points coincide. In which of the six possible cases does this imply that the triangle is equilateral?
Gy. 3165. In a teterahedron it can happen that an altitude goes outside the polytope. How many such altitudes may a tetrahedron have?
New problems in November 1997
F. 3196. Define a sequence an by a0=1, an+1=sin an (n=0,1,2,...). Prove that the sequence nan2 is bounded.
F. 3197. Some pieces are placed on an 8x8 chessboard such that there are exactly 4 pieces in each raw and coloumn of the board. Prove that there can be found 8 pieces among them such that no two of them are in the same row or coloumn.
F. 3198. The numbers
a1, a1, ..., an
are pairwise distinct positive integers. Prove inequality
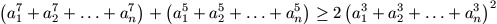 .
.
F. 3199. In a triangle ABC, the lines which divide the
angle at vertex C into n equal parts intersect AB
at points
C1, C2, ..., Cn-1
in this order. Prove that the value of fraction
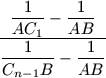 does not depend on n.
does not depend on n.
F. 3200. We are given two segments AB and CD. Fix AB and move CD around, in a position parallel to AB, such that quadrilateral ABCD is a trapezoid in which a circle can be inscribed. Determine the locus of the midpoints of the segments CD.
F. 3201. Let M be an arbitrary interior point of a tetrahedron ABCD. Let N, P, Q and A1, respectively, denote the intersection points of planes BCM, CDM, BDM, and BCD with lines AD, AB, AC and AM. Let finally D1, B1 and C1 denote the points where lines A1N, A1P and A1Q intersect the plane incident to A and parallel to BCD. Prove that A is the centroid of triangle B1C1D1.
New advanced problems in November 1997
ATTENTION! We correct and submit N. 146. again. (See KöMaL 1997/6.):
N. 146. Prove that any rational number 0<r<1 of odd
denominator can be expressed as the fraction part of a number of the form
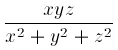 with suitable integers x,
y and z.
with suitable integers x,
y and z.
N. 152. There are given finitely many discs of unit radius in the plane such that the centres of any two of them are at least 10 units apart. Is it true that there exists a (not necessarily closed) polygon whose vertices are the centres of the given discs such that the polygon contains the centre of each disc, and each segment of the polygon intersects only those discs which are centered at its endpoints.
N. 153. The functions  are defined by
are defined by  ,
,
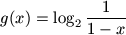 .
.
- a) Prove that f-g is bounded.
- b) Does the left-hand limit
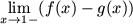 exist?
exist?N. 154. Colour each point of the plane according to the following
rule: the colour of the point (x; y) is white if
[x]+[y] is even, and is black otherwise. For arbitrary
positive integers a and b, consider the triangle with
vertices (0; 0), (0; a) and (b; 0); and denote by
f(a,b) the absolute value of the difference between
the areas of the white resp. black regions. Prove inequality
 , where un
denotes the nth term of the Fibonacci sequence, that is,
u1=1, u2=1,
un+2=un+un+1.
, where un
denotes the nth term of the Fibonacci sequence, that is,
u1=1, u2=1,
un+2=un+un+1.
