Exercises and problems in Physics
February 1998
New experimental problem:
m. 195. Pour the same amount and temperature (e.g. 80oC) of tea into different cups and measure the temperature decrease versus time. What does the speed of the cooling depend?New exercises:
FGy. 3129. We are trying to make an obtuse-angled triangle cut out of cardboard stand on a horizontal table plate. Is there such triangle that can only stand on one side? (The plane of the triangle is kept vertical.)
FGy. 3130. A load of power of 40 W is connected parallel to another load, thus the power decreases to 17 W. What is the power of the second load? (Provided the voltage and load resistance are kept constant.)
FGy. 3131. One mol of biatomic gas is being heated in a closed tank from 300 K up to 1000 K. During the process part of the molecules dissociate. At 1000 K the energy of the biatomic molecules are only half of that of the whole gas. How many molecules have dissociated and by what factor has the gas pressure risen? (The oscillation of the molecules are not to be taken in account.)
FGy. 3132. How many times greater is the work done by a gas
expanding at constant pressure, than of that which pressure is proportional
to its volume? The initial and final temperatures are the same.
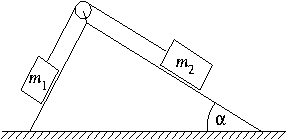
FGy. 3133. A frictionless pulley of negligible mass is attached to
the rectangular peak of a double sided slope with negligible friction on all
sides. A thread passing over the pulley connects bodies of mass
m1 and m1. Determine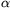 
versus m1 and m2 when
the slope does not slip on the vertical table with also negligible friction.
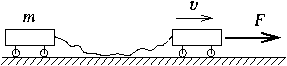
FGy. 3134. Two small carriages are connected by a thin elastic string of unstretched length of 96 cm and of force constant of 18 N/m which at first lies loosely on the ground. One of the carriages is being pulled by a constant velocity of 1.2 m/s.
- a) How long does it take the carriage of mass m=2 kg to catch up
with the carriage in front of it after the string has straightened?
- b) Make a graph versus time showing what force should be applied on the
first carriage to maintain a constant velocity.
- c) Determine the work needed.
- d) What is the distance covered by the second carriage?
New problems:
FF. 3135. An optical grid of grid constant of 2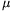
is illuminated with a perpendicular beam of monochromatic
light. Should this grid be replaced by one with half the original density,
so shall the first order diffraction angle decrease by 10.4o.
What is the wavelength of the light?
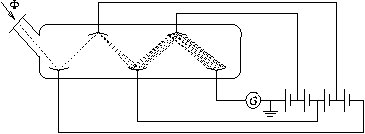
FF. 3136. The photoelectron multiplier which is able to transform
weak light intensity into electrical current measurable by a sensitive
galvanometer was invented by Z. Bay 60 years ago, in 1938. (The picture shows
the simplified model, the real one has 10-15 grades.) Ultraviolet light of
intensity 
and frequency f is
incident onto a photocathode of work function W. The electrons are
accelerated between the two electrodes by voltage U. If the losses
are negligible, what is the maximum number of electrons a photon can send
into the circuit? What is the maximum of the current flowing through the
galvanometer? (Data:
=10-10W,
f=2,2.1015Hz,
W=0,42.10-18J,
e=1,6.10-19C,
h=6,06.10-34Js,
U=4 V.)
FF. 3137. A particle of mass m is on a circuital orbit due to
force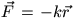 
of a central force field.
According to the Bohr theory determine the radius of the possible orbits and
the energy of the particle on these certain orbits.
FF. 3138. Due to the friction between the water and the crust of the Earth at the bottom of the oceans the maximum of the tide waves are not exactly pointed at the Moon. Does the tide hurry or delay in compare to the motion of the Moon? What effect does this have on the rotation of the Earth?
New advanced problem:
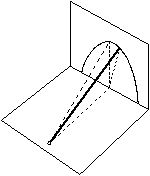
FN. 3139. An homogeneous rod may turn around a ball-and-socket joint attached to one end of it. The rod leans on a vertical wall and is in equilibrium when left alone. The upper end of the rod is then displaced by a little to the side and is left alone. At what position does the rod separate from the wall? (The friction by wall and the joint is negligible.)