Az 1999. októberi számban kitűzött B-jelű matematika feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B. 3302. Egy jegypénztárnál nyolcan állnak sorba. Négyüknél egy-egy 100 Ft-os, a másik négynél egy-egy 200 Ft-os van, sorrendjük véletlenszerű. A jegy ára 100 Ft, a kassza kezdetben üres. Mindenki egy jegyet szeretne vásárolni. A lehetséges sorrendek hányadrésze olyan, hogy a pénztáros fennakadás nélkül ki tudja adni a jegyeket? (3 pont)

Megoldásvázlat. Annak a feltételnek kell teljesülnie, hogy bármeddig nézzük a sort, mindig több 100-assal fizető embernek kell lennie, mint 200-assal fizetőnek. Ezt összeszámolva (felírva a lehetséges eseteket) azt kapjuk, hogy 14 ilyen eset van. Az összes esetek száma 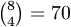. Tehát a válasz: .

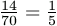B. 3303. Egy 5 cm széles papírcsíkot gyűrődés nélkül áthajtunk az ábra szerint.

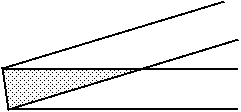
Milyen kicsi lehet a kétszer lefedett, satírozott rész területe? (4 pont)

Megoldásvázlat.

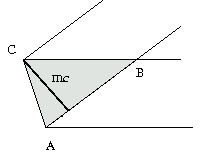
Az ABC háromszög területe AB^.m_c/2=AB^.5/2 cm. Mivel AB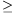5 cm, ezért a terület legkisebb lehetséges értéke 12,5 cm², és a 12,5 cm²-nél nagyobb értékek közül bármelyiket felveheti.

B. 3304. Meg lehet-e számozni egy kocka éleit az 1, 2, 3,..., 11, 12 számokkal úgy, hogy mindegyik csúcsban ugyanannyi legyen az ide befutó élekre írt számok összege? (4 pont)

Javasolta: Reményi Gusztáv, Budapest

Megoldásvázlat. Nem lehet.

Tegyük fel, hogy a kocka éleire ráírtuk az 1, 2, ..., 12 számokat. Ha minden csúcsban összeadjuk az élekre írt számokat, az így kapott összegek összegében minden él kétszer szerepel, ezért az összegek összege 2^.(1+2+...+12)=156, ami nem osztható a csúcsok számával, 8-cal.

B. 3305. Sándor Mátyás esetéből okulva, a hazafiak vezére egy egyenletet küldött barátainak:

2x²+4xy+7y²-12x-2y+N=0.

A titkos üzenet az volt, hogy a hónap N. napján legyen a felkelés. A hazafiak gyakran mondogatták, hogy a felkelés az egyetlen megoldás. Ez jellemzte N-et is: az egyenletet egyetlen (x,y) valós számpár elégítette ki. Mennyi N értéke? (4 pont)

1. megoldásvázlat. Ha az egyenletet x-re megoldjuk, akkor egy kivétellel minden y-ra negatívnak kell lennie a diszkriminánsnak, az egy kivételre pedig 0-nak. A diszkrimináns:

D(y) = (4y-12)²-4^.2^.(7y²-2y+N) = -8(5y²+10y+N-18).

Ez a kifejezés egyetlen y-ra 0, ezért ennek a diszkriminánsa is 0:

460-20N = 0,

azaz N=23. Ehhez az értékhez az y = -1, x = 4 megoldás tartozik.

2. megoldásvázlat. Rendezzük az egyenletet a következőképpen:

5(y+1)²+2(x+y-3)²=23-N.

Ennek az egyenletnek pontosan akkor van egy megoldása, ha 23-N=0, vagyis N=23.

B. 3306. Az egységnyi területű ABC háromszög AB oldalán a harmadolópontok legyenek D és E, az AC oldalán a felezőpont pedig F. A CB egyenesét az FE egyenes G-ben, az FD egyenes H- ban metszi. Határozzuk meg az FGH háromszög területét. (3 pont)

Megoldásvázlat. Legyen P a BC szakasz felezőpontja, BC=a, AC=b.

A párhuzamos szelők tételéből GB : GP = BE : PF = 2 : 3 és HP : HB = PF : BD = 3 : 4, ezekből GB=HC=a.

Az FGH háromszög GH alapja háromszor akkora, mint a BC oldal, az ehhez tartozó magassága fele az ABC háromszög A-ból induló magasságának, tehát az FGH háromszög területe 1,5-szerese az ABC háromszög területének.

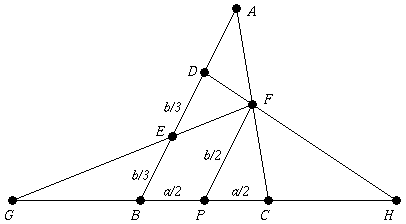
B. 3307. Határozzuk meg az ábrán látható MAN, MBN, MCN, MDN, MEN szögek összegét, ha tudjuk, hogy PA=AB=BC=CD=DE. (3 pont)

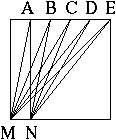
Orosz versenyfeladat

Megoldásvázlat.

MAN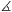 =AMP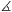, és a többi szögnek is megvan az Acsúcsú párja, így az öt szög összege egyenlő A PME szöggel, ami 45^o.

B. 3308. Hány olyan ikerprím számpár van, amelyek összege prímhatvány? (Ikerprímnek nevezünk két prímszámot, ha a különbségük 2.) (4 pont)

Javasolta: Kovács Ádám, Budapest

Megoldásvázlat. Ha a két prímszám 3-nál nagyobb, akkor a kisebbik 6k-1, a nagtobbik 6k+1 alakú, és ezért az összegük osztható 6-tal, nem lehet prímhatvány. Ezért az egyetlen megoldás a 3 és az 5.

B. 3309. Egy kocka minden lapján kijelöltük a középvonalak negyedelőpontjait. Hogyan aránylik a pontok által meghatározott test térfogata a kocka térfogatához? (4 pont)

Megoldásvázlat.

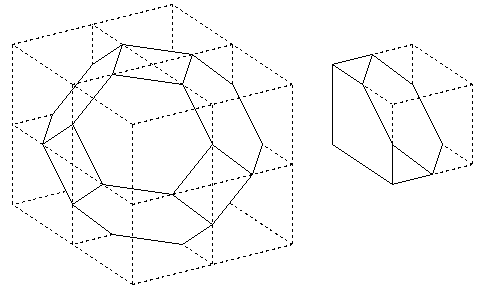
Vágjuk a nagy kockát 8 egybevágó kis kockára. Ekkor minden kis kockát az új test lapjai szabályos hatszögben metszenek. (Gy.3237-es feladat.) A kis kockákat ez a metszés két egybevágó részre vágja. Ezért a keresett arány 1:2.

B. 3310. Mutassuk meg, hogy az (x²+y²)³=27x²y² egyenletű görbe belefoglalható egy 4 egység oldalú négyzetbe. (5 pont)

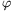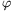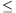
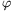
Megoldásvázlat. Legyen x=rcos és y=rsin, ahol r>0 és 0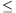2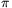. Az egyenletbe behelyettesítve

r⁶=27r⁴sin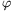²cos²,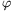

r²=27sin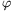²cos²,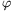

végül, a számtani és mértani közép közötti egyenlőtlenséget is felhasználva,

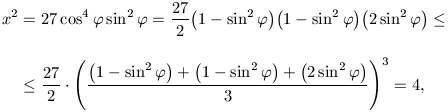
|x|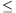2.

Teljesen hasonlóan kapjuk, hogy |y|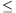2.

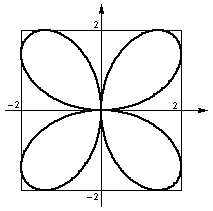
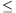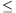A görbe összes pontja a -2x,y2 négyzetben van.

B. 3311. Igazoljuk, hogy ha 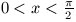, akkor

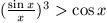
(5 pont).

Kovács Ádám (Budapest) ötletéből

Megoldásvázlat. Az egyenlőtlenséget átrendezve,

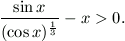
Az x=0 esetben a baloldal értéke 0, ezen kívül megmutatjuk, hogy a baloldal a 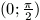intervallumban szigorúan monoton nő.

A baloldal deriváltja

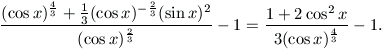
A számtani és mértani közép közötti egyenlőtlenség alapján

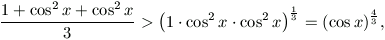
vagyis a derivált pozitív.