Exercises and problems in Physics February 2000

Please read The Conditions of the Problem Solving Competition.

New experimental problem:

M. 213. Measure the radiation pattern of a microphone.

New problems:

P. 3315. A child asks: `Why does winter come when the Earth gets nearest to the Sun?' Answer his question. (3 points)

P. 3316. I wanted to project the spectrum of a sunbeam onto the wall using a regular (equilateral triangle-based) prism with a medium refractive index of n=1.5. I was turning the prism so that the sunbeam be perpendicular to its edge when I noticed the spectrum appearing on the floor, but in a reversed order. Why? At what angles of incidence are both spectra present? (4 points)

P. 3317. What is the maximum possible height of a column made of -0.1 ^oC ice cubes? (4 points)

P. 3318. The ends of a thread of length L are fixed at identical heights, at distance D from each other. A small bead can slide on the thread without friction. What is the period of the bead for small deviations if a) the deviation is perpendicular to the plane of the thread; b) the deviation is within the plane of the thread? (5 points)

P. 3319. A narrow electron beam accelerated in vacuum using a voltage of U=250 V produces a magnetic induction of B=8^.10^-6 T at r=2 mm from its axis. What force does the electron beam exert onto a metal plate placed in its way? Assume that 20 % of the electrons is elastically reflected and the rest is absorbed by the plate. (4 points)

P. 3320. 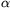 particles and C and Ca nuclei with negligible initial velocity are accelerated in a heavy ion accelerator using the same voltage. What is the ratio of their final velocities? Does the result depend on the magnitude of the accelerating voltage? (4 points)

P. 3321. Measurements of scattering indicate that all the nucleons in a nucleus of mass number A are within a sphere of radius r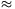A^1/3.1.2^.10^-13 cm, close to each other. Calculate the density of the nucleus. What is the diameter of a star of such average density and with a mass identical to that of the Sun? What is the escape velocity at the surface of such a star? (4 points)

P. 3322. An electrically charged small bead can move without friction in a horizontal plane on a circular insulating wire. There is a fixed dipole with a horizontal axis at the centre of the circle. The bead is initially at rest at a position perpendicular to the axis of the dipole. a) What force does the bead exert onto the wire during its motion? b) Where does the bead first stop after being released? c) What trajectory would the bead follow in the horizontal plane if it were not strung onto the wire? (6 points)

P. 3323. The magnitude of the initial velocity of an intercontinental ballistic missile is half of the first cosmic velocity, its direction includes an angle of 45^o with the horizontal plane. a) What are the major and minor axes of the orbit of the missile? b) What maximum height does the missile reach above the surface of the Earth? c) How far from its starting place does it reach the ground? d) How long does the missile remain in movement? (Take no notice of the rotation of the Earth.) (6 points)