A 2000 márciusi A-jelű matematika feladatok megoldása

A. 233. Definiáljuk az (a_n) sorozatot a következőképpen: a₀=a₁=1, (n+3)a_n+1=(2n+3)a_n+3na_n-1. Mutassuk meg, hogy a sorozat egész számokból áll.

Megoldásvázlat. A rekurzió alapján a sorozat első néhány eleme: a₀=1, a₁=1, a₂=2, a₃=4, a₄=9, a₅=21, a₆=51, a₇=127, a₈=323, a₉=835, a₁₀=2188.

Bebizonyítjuk, hogy tetszőleges n nemnegatív egészre

(2)    a_n+2=a_n+1+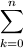a_ka_n-k.

Ebből a feladat állítása azonnal következik.

A (2) azonosság n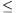8-ra leellenőrizhető a fenti adatok alapján, például n=4 esetén

a₅+a₀a₄+a₁a₃+a₂a₂+a₃a₁+a₄a₀ = 21+1^.9+1^.4+2^.2+4^.1+9^.1 = 51 = a₆.

A (2) azonosságot n szerinti teljes indukcióval bizonyítjuk. Az n=0,1,2 esetekben behelyettesítéssel ellenőrizhető. Tegyük fel, hogy (2) igaz n<m-re, ahol m3; ebből bebizonyítjuk az n=m esetre is. Az indukciós feltevés és az (1) rekurzió többszöri felhasználásával

(m+4)(a_m+1+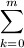a_ka_m-k)=

=(m+4)a_m+1+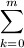(k+2)a_ka_m-k+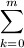(m-k+2)a_ka_m-k=

=(m+4)a_m+1+(2a₀a_m+3a₁a_m-1+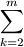((k+2)a_k)a_m-k) +(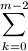a_k((m-k+2)a_m-k)+3a_m-1a₁+2a_ma₀)=

=(m+4)a_m+1+4a_m+6a_m-1+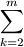((2k+1)a_k-1+3(k-1)a_k-2)a_m-k +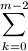a_k((2m-2k+1)a_m-k-1+3(m-k-1)a_m-k-2)=

=(m+4)a_m+1+4a_m+6a_m-1+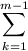(2k+3)a_ka_m-1-k+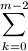3(k+1)a_ka_m-2-k +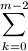(2m-2k+1)a_ka_m-1-k+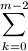3(m-k-1)a_ka_m-2-k=

=(m+4)a_m+1+4a_m+6a_m-1 +((2m+4)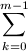a_ka_m-1-k-6a₀a_m-1)+3m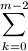a_ka_m-2-k=

=(m+4)a_m+1+4a_m+(2m+4)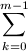a_ka_m-1-k +3m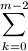a_ka_m-2-k=

=(m+4)a_m+1+4a_m+(2m+4)(a_m+1-a_m)+3m(a_m-a_m-1)=

=(3m+8)a_m+1+ma_m-3ma_m-1=

=((2m+5)a_m+1+3(m+1)a_m)+((m+3)a_m+1-(2m+3)a_m-3ma_m-1)=

=(m+4)a_m+2+0=(m+4)a_m+2.

Megjegyzések.

1. A (2) azonoságot nem csak próbálgatással lehet megtalálni. Tekintsük az

f(x)=a₀+a₁x+a₂x²+...

függvényt. (Nem nehéz végiggondolni, hogy a_n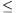3ⁿ, és ezért a hatványsor konvergens |x|<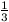 esetén.) Az (a_n) sorozat definíciójából megállapítható, hogy az f függvényre teljesül a következő differenciál-egyenlet:

(3)    f(0)=1,  (x-2x²-3x³)f'(x)+(2-3x-3x²)f(x)+2=0.

A (3) egyenletet megoldva (fáradságos, de megéri) kapjuk, hogy

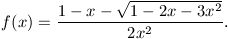
Ezt átrendezve pedig az

(4)    x²f²(x)+(x-1)f(x)+1=0

azonosságot kapjuk. A (4) azonosságban az együtthatók vizsgálatából kapjuk a (2) azonosságot.

2. Az (a_n) sorozat egy másik előállítása:

Itt 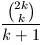egész, ez az úgynevezett k-adik Catalan-szám.

A. 234. Az A, B, és C betűk felhasználásával szavakat (véges hosszúságú betűsorozatokat) készítünk. Egy szóval a következő műveleteket végezhetjük:

a) A szóban kiválasztunk néhány egymás utáni betűt - esetleg csak egyetlen egyet, vagy akár a teljes szót -, és ,,megduplázzuk'', például BBCAC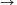BBCABCAC;

b) Az a) lépés visszafelé: Ha valahol a szóban két egymás utáni részlet megegyezik, akkor az egyiket elhagyjuk: ABCABCBC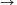ABCBC.

Igazoljuk, hogy ilyen lépések sorozatával bármelyik szóból eljuthatunk egy legfeljebb 8-betűs szóhoz.

Megoldásvázlat. Ha az u és v szavak átalakíthatók egymásba, azt így fogjuk jelölni: uv, és azt mondjuk, hogy a két szó ekvivalens. Az u és v szavak egymás után írását pedig uv-vel jelöljük.

Először bebizonyítjuk a következő lemmát.

Lemma. Ha az u szó az A, B, C betűk mindegyikét tartalmazza, akkor tetszőleges v szóhoz létezik olyan w szó, amelyre uvwu.

Bizonyítás. Ha v csak egyetlen betű, akkor - mivel u ezt a betűt is tartalmazza -, u felírható u=u₁vu₂ alakban; ekkor legyen w=u₂. Ezzel a választással

uvw=(u₁vu₂)vu₂=u₁((vu₂)(vu₂))u₁(vu₂)=u.

Az általános esetben legyenek v betűi sorrendben a₁,...,a_k. Mint láttuk, választhatók olyan w₁,...,w_k szavak, amelyekre (ua₁)w₁u, (ua₁a₂)w₂ua₁, ...,(ua₁...a_k)w_kua₁...a_k-1. Ekkor

uua₁w₁ua₁a₂w₂w₁...ua₁...a_kw_k...w₁=uv(w_k...w₁),

vagyis w=w_k...w₁ egy jó választás. Ezzel a lemmát igazoltuk.

Legyen most a egy olyan szó, amely legalább 9 betűből áll. Megmutatjuk, hogy ez ekvivalens egy rövidebb szóval.

Legyen a=bcd, ahol b az első 4 betűt tartalmazza, d pedig az utolsó 4-et. Könnyű ellenőrizni, hogy ha b vagy d csak kétféle betűből áll, akkor tartalmaz két megegyező, egymás utáni részletet, és ilyenkor a b) lépés közvetlenül alkalmazható.

Ha b és d mindhárom fajta betűt tartalmazza, akkor megmutatjuk, hogy abd. A lemma alapján létezik egy olyan e szó, amelyre b(cd)eb, és létezik egy olyan f szó is, amelyre defd. Ezek felhasználásával

a=bcdbc(def)bc(dedef)=(bcde)(def)bd.

Megjegyzések. 1. Nem minden 9-betűs szó hossza csökkenthető csupán a b) lépéssel. Sőt, akármilyen hosszú szó készíthető, amelyben nincs két egymás utáni megegyező részlet.

2.Egy lehetséges megoldás, ha a szavak kezdeteit vizsgálva minden esetre megadunk egy eljárást, amellyel a legalább 9-betűs szavak hossza csökkenthető, Pl.

AAxAx;
ABAAxABAx;
ABABxABx;
ABACAAxABACAx;
ABACABAAxABACABAx;
ABACABABxABACABx;
ABACABACxABACx;
ABACABBxABACABx;
...

ABACBCACBABACBCACBCBABACBCB.

(Az utolsó szó tovább rövidíthető az ABACB szóvá.)

A fennmaradó esetekben több lépésre van szükség. A megoldásban látott algoritmus ezekre nem a legrövidebb megoldást adja, pl. az a=ABCBACABC, szóra alkalmazva b=ABCB, c=A, d=CABC, e=ABACACBABCB és f=CBABACBACACACABABCABC. A leghosszabb szó, amelyre az eljárás során szükség van, a 46-betűs

bcdedef = ABCBACABCABACACBABCBCABCABACACBABCBCBABACBACACACABABCABC

szó. Ugyanakkor az ABCBACABC szó egyszerűbben is lerövidíthető, például

(1) ABCBACABCABCBACABCBCABCBACABCBABCBCABCBACABCBACBABCBCABCBACBABCABCBABC.

A. 235. Legyen a adott komplex szám. Mi a mértani helye azon b komplex számoknak, amelyekhez léteznek olyan nemnegatív x₁,x₂,...,x_n valós számok és egységnyi abszolút értékű z₁,z₂,...,z_n komplex számok, hogy x₁+x₂+...+x_n=1, x₁z₁+x₂z₂+...+x_nz_n=a és x₁z₁²+x₂z₂²+...+x_nz_n²=b?

Megoldásvázlat. Legyen b=p₁z₁²+...+p_nz_n². Megjegyezzük, hogy a és b abszolút értéke is legfeljebb 1 lehet, mivel egységnyi komplez számok súlyozott átlagai.

Azt állítjuk, hogy a keresett halmaz az a² középpontú, 1-|a|² sugarú körlemez.

Először is megmutatjuk, hogy b biztosan eleme a körlemeznek. Legyen 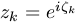. Ekkor tetszőleges 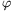szögre, felhasználva a cos 2t=1-2sin²t azonosságot, a súlyozott számtani és négyzetes közép közötti egyenlőtlenséget valamint a Re z²=(Re z)²-(Im z)² azonosságot,

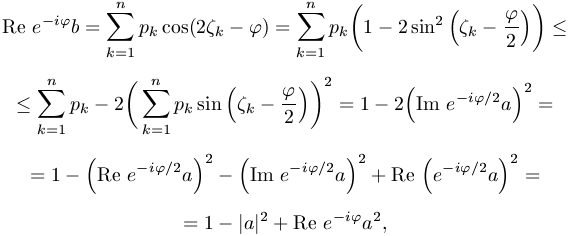
vagyis

(1)    

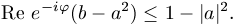
Ha 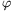-t éppen b-a² argumentumának választjuk, akkor (1) baloldalán |b-a²| áll. Ezért |b-a²|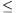1-|a|², vagyis b eleme az a² középpontú, 1-|a|² sugarú zárt körlemeznek.

Most megmutatjuk, hogy ha |b-a²|=1-|a|², akkor léteznek olyan p₁, p₂ nemnegatív valós számok és z₁, z₂ egységnyi abszolút értékű komplex számok, amelyekre p₁+p₂=1, p₁z₁+p₂z₂=a és p₁z₁²+p₂z₂²=b, vagyis a körlemez határpontjai megfelelőek.

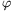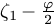Legyen a b-a² szám argumentuma , és vizsgáljuk meg, hogy (2)-ben mikor áll egyenlőség. Az egyenlőséghez szükséges és elegendő, ha a és 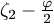szögek szinusza megegyezik; feltehetjük, hogy alkalmas 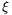szöggel és 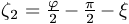. Ezekre a számokra teljesülnie kell, hogy

(2)  

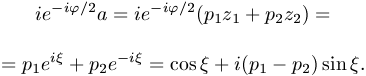
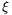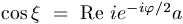Láthatjuk, hogy -t úgy kell választanunk, hogy teljesüljön. Ez nyilván lehetséges, mert (2) baloldalának abszolút értéke, |a| legfeljebb 1. Ezután meghatározzuk a p₁-p₂ együtthatót úgy, hogy (2) két oldalának képzetes része is megegyezzen. Ismét csak amiatt, hogy a baloldal legfeljebb egységnyi abszolút értékű, |p₁-p₂| nem lehet nagyobb 1-nél. Végül p₁-p₂ és p₁+p₂=1 ismeretében meghatározzuk a p₁ és p₂ számokat. A kapott p₁ és p₂ nem lehet negatív |p₁-p₂|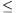1 miatt.

Az ilyen módon konstruált p₁, p₂, z₁, z₂ számokra a konstrukció szerint p₁z₁+p₂z₂=a. Felhasználva, hogy 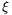definíciójából

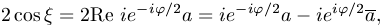
valamint tetszőleges t-re e^2it+1=2e^itcos t,

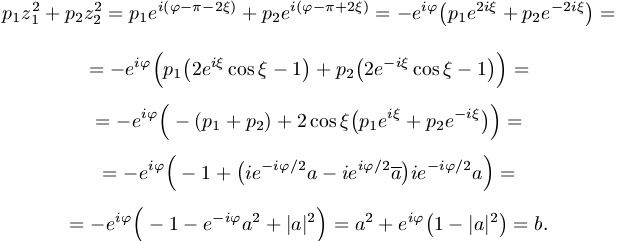
Végül megmutatjuk, hogy a körlemez tetszőleges b pontjához léteznek a feltételeknek megfelelő p₁, p₂, p₃, p₄ és z₁, z₂, z₃, z₄ számok.

Húzzunk egy tetszőleges egyenest b-n keresztül; messe ez a kör kerületét b₁-ben és b₂-ben. Ekkor b=q₁b₁+q₂b₂ alkalmas q₁, q₂ nemnegatív számokkal, amelyekre q₁+q₂=1.

Az előbbieket a b₁ és b₂ számokra alkalmazva, léteznek olyan x₁, y₂, y₃, y₄ nemnegatív valós számok és egységnyi abszolút értékű z₁, z₂, z₃, z₄ komplex számok, amelyekre x₁+x₂=x₃+x₄=1, x₁z₁+x₂z₂=x₃z₃+x₄z₄=a, x₁z₁²+x₂z₂²=b₁, végül x₃z₃²+x₄z₄²=b₂. Ugyanezekkel a z₁, z₂, z₃, z₄ számokkkal és a p₁=q₁x₁, p₂=q₁x₂, p₃=q₂x₃, p₄=q₂x₄ választással

p₁+p₂+p₃+p₄=q₁(x₁+x₂)+q₂(x₃+x+4)=q₁+q₂=1,

x₁z₁+p₂z₂+p₃z₃+p₄z₄=q₁(x₁z₁+x₂z₂)+q₂(x₃z₃+x₄z₄)=q₁a+q₂a=a,

x₁z₁²+p₂z₂²+p₃z₃²+p₄z₄²=q₁(x₁z₁²+x₂z₂²)+q₂(x₃z₃²+x₄z₄²)=q₁b₁+q₂b₂=b.

A p₁z₁²+...+p_nz_n² lehetséges értékeinek mértani helye a komplex számsíkon tehát az a² középpontú, 1-|a|² sugarú, zárt körlemez.