New exercises and problems in Mathematics
November 2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in November 2000 |
C. 600. We are travelling in a car by constant velocity from Budapest to Kosice. Passing by a kilometre mark we notice a two-digit number on it. After half an hour we reach at another mark which shows the same two digits in the reverse order. After another 30 minutes of travelling we notice the same two digits again, but this time there is also a 0 digit on the sign. Determine the velocity of the car.
C. 601. Solve the equation 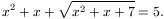
Proposed by: N. Gyanta, Budapest
C. 602. A large solid cube is built of identical smaller cubes such that more than half of the small cubes are not visible from outside. At least how many small cubes are used to build the large cube?
C. 603. Determine the range of the function f(x)=(x2+x+1)/(x2+1).
C. 604. Given a triangle ABC whose incenter is
O, and its area is t. Prove that 2t=AO2sin 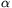 +BO2sin
+BO2sin 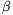 +CO2sin
+CO2sin 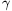 .
.
Proposed by: S. Mihalovics, Esztergom
 |
New problems in Oktober 2000 |
B. 3402. The students of two schools were sitting the same test. The students attending the first school scored 74 on average; within this the average scores of the boys and the girls were 71 and 76, respectively. The corresponding scores in the other school were 84, 81 and 90, respectively. If the average score of all boys was 79, what did the girls score on average? (3 points)
B. 3403. Given that the real numbers a,
b, c satisfy 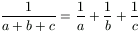 , prove that
, prove that
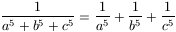 (3 points)
(3 points)
Proposed by: T. Székelyhidi, Ercsi
B. 3404. In a cube with ten-unit long edges, let A, B and C denote the endpoints of three edges starting from the same vertex. Two planes S1 and S2, parallel to the plane ABC, divide the cube into three parts whose volumes are in the ratio 251:248:251. Calculate the distance between the two planes. (5 points)
B. 3405. Five marbles are to be measured with the help of a one-armed balance. We are allowed to perform nine weighings and each time we may put either one or two marbles on the scale. It may happen, however, that one of the results is misread. Is it still possible to determine the weight of each marble? (4 points)
Proposed by: L. Surányi, Budapest
B. 3406. For each vertex (x,y) of a polygon x and y are positive integers such that x|2y+1 and y|2x+1. Find the maximum area of such a polygon. (4 points)
Proposed by: S. Mihalovics, Esztergom
B. 3407. Arnold, Bob, Chris, Dorothy, Eric and Frank are to play Dungeons and Dragons again. They have not appointed the Dungeon Master yet. The following method is used to select the Dungeon Master. They throw the 10 sided die used in the game one by one in a given order. The one who throws the first 1 or 2 is the Dungeon Master. If, by the end of the round, they still do not have the Dungeon Master, they start again in the same order until someone finally throws 1 or 2. Dorothy has never been a Dungeon Master yet, and now she is really excited about that. The guys are really polite and let her choose her position in the order of throws. What would you advise Dorothy? (3 points)
Proposed by: Gy. Pogány, Szolnok
B. 3408. An integer is assigned to each vertex of a regular 2n-gon such that numbers assigned to neighbouring vertices always differ by 1. Numbers that are larger than both of their neighbours are called mountains and the ones which are smaller than their neighbours are called valleys. Prove that the sum of the mountains minus the sum of the valleys is n. (5 points)
Proposed by: A. Hraskó, Budapest
B. 3409. Reflect the parabola y=x2 in the point (1,1) and determine the equation of its image. (3 points)
B. 3410. A large painting, three metres in height, hangs on a vertical wall and the lower edge is one metre above the observer's eye level. The best view of the painting is assumed to be when the angle subtended by the painting at the observer's eye is a maximum. Calculate how far from the wall the observer should stand to maximize this angle. (4 points)
B. 3411. A regular polygon approximates the area of its circumcircle with a relative error less than one thousandth. Find the minimum number of sides such a polygon should have. (4 points)
 |
New advanced problems in November 2000 |
A. 248. Consider partitions of the power set of an n-element set into two parts I and H such that the following conditions are simultaneously satisfied:
- a) a
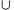 b
b I and a
I and a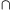 b
b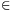 I for any a, b
I for any a, b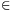 I;
I;
b) a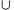 b
b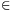 H and a
H and a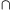 b
b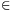 H for any a,b
H for any a,b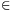 H;
H;
c) a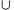 b
b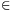 I and a
I and a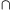 b
b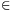 H for any a
H for any a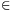 I,
b
I,
b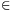 H.
H.
How many such partitions are there? (The power set of a set is the set of all its subsets.)
Proposed by: E. Csirmaz, Budapest
A. 249. Let a, b, c, t be positive numbers such that abc=1. Prove that
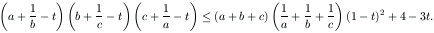
A. 250. A horizontal board is a support for four
vertical pegs. One of the pegs passes through holes in n disks of
increasing size, the largest disk being at the bottom, the smallest one on the
top. We may take disks off a peg, always one at a time, and put each disk on
another peg, but never in such a way that a disk is put on top of a smaller
disk. Prove that the minimum number of transfers one should make to transfer
all the disks to another peg is at least 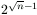 but less than
but less than 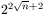 .
.
Based on a problem proposed by B. Énekes, Tolna
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.
