A 2000 decemberi A-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 251. Adott a térben egy gömb. Ha a P pont illeszkedik a gömbre, a Q pont pedig nem, akkor jelölje PQ a PQ egyenes és a gömb P-től különböző metszéspontját. Ha a PQ egyenes érinti a gömböt, akkor legyen PQ=P.
Igazoljuk, hogy ha a gömb A, B, C, D pontjai nincsenek egy síkban, akkor legfeljebb két olyan Q pont létezik, amelyre az AQBQCQDQ tetraéder egyenlő oldalú. (Egy tetraédert egyenlő oldalúnak nevezünk, ha a lapjai egybevágóak.)
Megoldásvázlat. Legyen Q egy, a feltételeknek megfelelő pont, és legyen a gömbre vonatkozó hatványa p. Tekintsük az A, B, AQ és BQ pontokat.

Az ABQ és BQAQQ háromszögek hasonlóságából
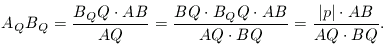
Ugyanígy kapjuk, hogy
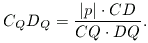
Mivel az AQBQCQDQ tetraéder egyenlő oldalú, AQBQ=CQDQ. Behelyettesítve az előbbi eredményeket,
(1) 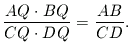
Teljesen hasonlóan
(2) 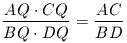
és
(3) 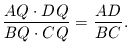
Az (1), (2) és (3) egyeneletekből kiszámíthatjuk az AQ, BQ, CQ és DQ távolságok arányát:
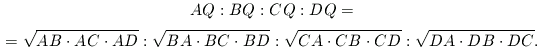
Azok a Q pontok, amelyekre az AQ:BQ arány megfelelő, egy gömbön vannak, amelynek középpontja az AB egyenesen van. (Ha az arány 1, akkor a gömb elfajul az AB szakasz felező merőleges síkjává.) Az összesen 6 gömb középpontjai az ABCD tetraéder élegyenesein vannak, ezért nem lehetnek egy egyenesen. A gömböknek emiatt legfeljebb két közös pontja lehet. (Abban az esetben, ha egy vagy több gömb síkká fajul, további diszkusszióra van szükség.)
A. 252. Igazoljuk, hogy ha az a1,...,an egész számok (n+k)-val osztva összesen legalább k+1 különböző maradékot adnak, akkor kiválasztható közülük néhány (lehet, hogy csak egy; lehet, hogy az összes), amelyek összege osztható (n+k)-val.
Javasolta: Károlyi Gyula és Podoski Károly, Budapest
Megoldásvázlat. A szimmetria miatt feltehetjük, hogy a1,...,ak+1 páronként különböző maradékot ad (n+k)-val osztva. Legyen S=a1+...+ak+1, és tekintsük a következő három számhalmazt:
| I. | a1, a2, ..., ak+1; |
|---|---|
| II. | S-a1, S-a2, ..., S-ak+1; |
| III. | S, S+ak+2, S+ak+2+ak+3, ..., S+ak+2+...+an |
Ez összesen n+k+2 összeg. Ha valamelyik osztható (n+k)-val, kész vagyunk. A továbbiakban feltételezzük, hogy egyik sem osztható (n+k)-val.
Az a1,...,ak+1 számok kiválasztása miatt az I. sorozatban a számok páronként különböző maradékot adnak (n+k)-val osztva. Ugyanez igaz a II. sorozatra is.
Könnyen ellenőrizhető, hogy ha a három sorozatból valamelyik két
szám kongruens modulo (n+k), de a különbségük nem írható
fel néhány ai
összegeként, az csak úgy lehetséges, ha az egyik szám
aj, a másik pedig
S-aj valamely
alkalmas 1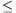 j
j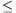 k+1 indexre. Mivel a sorozatokban összesen
n+k+2 szám van, de csak n+k-1 lehetséges
maradék (a 0-t kizártuk), vagy három ilyen j index létezik,
vagy pedig kiválasztható néhány ai, aminek az összege osztható
(n+k)-val.
k+1 indexre. Mivel a sorozatokban összesen
n+k+2 szám van, de csak n+k-1 lehetséges
maradék (a 0-t kizártuk), vagy három ilyen j index létezik,
vagy pedig kiválasztható néhány ai, aminek az összege osztható
(n+k)-val.
Viszont S-aj aj
(mod n+k), azaz 2aj
aj
(mod n+k), azaz 2aj S (pmod n+k) legfeljebb kétféle
j esetén teljesülhet, mert a 2x
S (pmod n+k) legfeljebb kétféle
j esetén teljesülhet, mert a 2x S (pmod n+k) kongruenciának
legfeljebb két megoldása lehet.
S (pmod n+k) kongruenciának
legfeljebb két megoldása lehet.
A. 253. Keressük meg az összes olyan f:(0,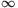 )
)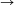 (0,
(0,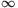 ) függvényt, amelyre tetszőleges x,
y pozitív valós számok esetén
) függvényt, amelyre tetszőleges x,
y pozitív valós számok esetén
(1) f(x)f(yf(x))=f(x+y).
Megoldás. Először bebizonyítjuk, hogy tetszőleges x
esetén f(x)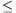 1. Tegyük
fel, hogy valamely x-re f(x)>1. Ehhez
találhatunk olyan pozitív y-t, amelyre
yf(x)=x+y: ez a szám az
1. Tegyük
fel, hogy valamely x-re f(x)>1. Ehhez
találhatunk olyan pozitív y-t, amelyre
yf(x)=x+y: ez a szám az 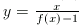 . Behelyettesítve ezeket az értékeket (1)-be,
. Behelyettesítve ezeket az értékeket (1)-be,
f(x)f(x+y)=f(x)f(yf(x))=f(x+y),
amiből f(x)=1, ez pedig ellentmondás.
Az (1) egyenletben az f(yf(x)) tényező minden
esetben legfeljebb 1; ebből következik, hogy tetszőleges x,y
számokra f(x+y)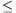 f(x), vagyis az f függvény
monoton fogy.
f(x), vagyis az f függvény
monoton fogy.
Most megmutatjuk, hogy a függvény vagy konstans 1, vagy pedig minden értéke kisebb 1-nél. Ha valamely x>0-ra f(x)=1, akkor az egyenletből f(2x)=f(x+x)=f(x)f(xf(x))=1. Ezt a lépést ismételgetve kapjuk, hogy f(4x), f(8x), ...mindegyike 1. A monotonitás miatt az ezeknél kisebb helyeken is csak 1 lehet a függvény értéke. Ha tehát a függvény legalább egyszer felveszi az 1-et, akkor konstans 1.
A konstans 1 függvényre teljesül az (1) függvényegyenlet. A továbbiakban azt az esetet vizsgáljuk, ha f mindegyik értéke kisebb 1-nél. Az ilyen függvényekre az előbbi módon kapjuk, hogy szigorúan monoton fogynak.
Legyen f(1)=a; tetszőleges t>0 esetén
helyettesítsük be (1)-be az x=1, 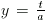 illetve x=t,
illetve x=t, 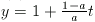 számokat,
számokat,
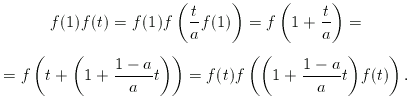
f(t)-vel osztás után, a szigorú monotonitásból kapjuk, hogy
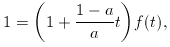
amiből
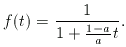
Bevezetve a 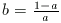 jelölést,
jelölést, 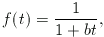 ahol b>0. Behelyettesítéssel
ellenőrizhető, hogy az ilyen alakú függvények is megoldások. A
b=0 elfajuló eset a konstans 1 függvényt adja. Az összes
megoldás tehát:
ahol b>0. Behelyettesítéssel
ellenőrizhető, hogy az ilyen alakú függvények is megoldások. A
b=0 elfajuló eset a konstans 1 függvényt adja. Az összes
megoldás tehát:
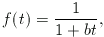
ahol b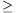 0.
0.

