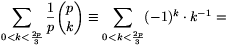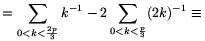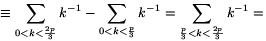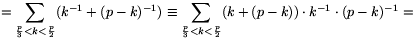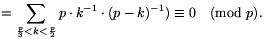A 2001 szeptemberi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 269. Egy kör keresztmetszetű lyukat két 1 méter oldalú négyzetlappal szeretnénk hézagmentesen lefedni. Milyen határok között mozoghat a lyuk átmérője?

Megoldás. Könnyen ellenőrizhető, hogy egy $\displaystyle 2-\sqrt2$ sugarú kör (és minden ennél kisebb sugarú is) lefedhető két egységnyi oldalú négyzetlappal az 1. ábrán látható módon.

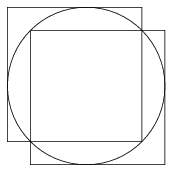
1. ábra

A továbbiakban megmutatjuk, hogy ha egy r sugarú körvonalnak egy egységnyi oldalú négyzetlap legalább a felét lefedi, akkor $\displaystyle r\le2-\sqrt2$. Ebből következik, hogy ($\displaystyle 2-\sqrt2$)-nél nagyob sugarú kört már nem lehet két egységnégyzettel lefedni.

Legyen tehát K egy r sugarú körvonal, N pedig egy egységnyi oldalú négyzetlap, amely lefedi K-nak legalább a felét. Ha r$\displaystyle ge$1/2, akkor az N-et eltolhatjuk párhuzamosan úgy, hogy minden oldalegyenesének legyen közös pontja K-val, miközben a K-ból lefedett rész csak bővül (2. ábra).

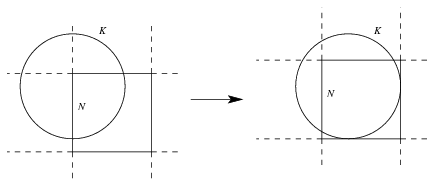
2. ábra

Elég tehát azokkal az esetekkel foglalkozni, amikor r>1/2 és K-nak az N mindegyik oldalegyenesével van közös pontja.

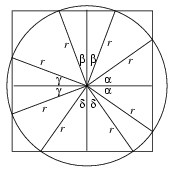
Megmutatjuk, hogy ha az N valamelyik csúcsa a K belsejébe esik, akkor N nem fedheti le K-nak a felét. Legyenek N csúcsai A, B, C, D; ezek közül az A essen K belsejébe. Az AB és AD félegyenesek messék K-t a P, illetve Q pontban (3. ábra).

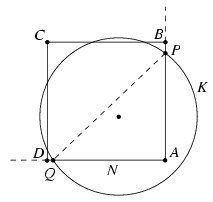
3. ábra

Mivel PAQ$\displaystyle angle$=90^o, a K kör középpontja a PQ egyenesnek ugyanarra a partjára esik, mint az A csúcs, és emiatt az A csúccsal azonos oldalon levő PQ körív hosszabb, mint egy félkör. Ez az ív pedig teljes egészében N-en kívül halad.

Mindezek után már csak egy esetet kell megvizsgálnunk: amikor N mindegyik csúcsa K-n kívülre vagy a határára esik, ugyanakkor K-nak az N mindegyik oldalegyenesével van közös pontja. Könnyen ellenőrizhető, hogy a közös pontok nem lehetnek az oldalak meghosszabbításain, hanem csak N kerületén.

Jelöljük $\displaystyle alpha$, $\displaystyle beta$, $\displaystyle gamma$, $\displaystyle delta$-val a 4. ábrán megjelölt szögeket.

4. ábra

A le nem fedett ívek hossza legfeljebb K kerületének fele, tehát $\displaystyle alpha$+$\displaystyle beta$+$\displaystyle gamma$+$\displaystyle delta$ $le$ 90^o. A szimmetria miatt feltehetjük, hogy $alpha$ + $gamma$ $le$ 45^o.

Mint az ábráról is leolvasható, r(cos $alpha$ +cos $gamma$ )=r(cos $beta$ +cos $delta$ )=1. Ebből és a koszinuszfüggvény konkávitásából

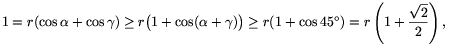
$1=r(\cos\alpha+\cos\gamma)\ge r\big(1+\cos(\alpha+\gamma)\big)\ge r(1+\cos45^\circ)=r\left(1+{\sqrt2\over2}\right),$

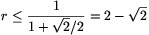tehát $r\le{1\over1+\sqrt2/2}=2-\sqrt2$ .

A lefedett lyuk sugara tehát legfeljebb 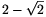$2-\sqrt2$ , átmérője legfeljebb 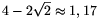$4-2\sqrt2\approx1,17$ méter lehet.

A. 270. Igazoljuk, hogy tetszőleges a, b, c, d pozitív számokra

(1)	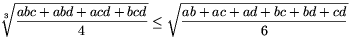$\root3\of{abc+abd+acd+bcd\over4}\le\sqrt{ab+ac+ad+bc+bd+cd\over6}$

1. megoldás. Definiáljuk a következő, az a, b, c, d változókban szimmetrikus mennyiségeket:

S₃₃=a³b³+a³c³+a³d³+b³c³+b³d³+c³d³;

S₃₂₁=a³b²c+a³b²d+...+bc²d³;

S₃₁₁₁=a³bcd+ab³cd+abc³d+abcd³;

S₂₂₂=a²b²c²+a²b²d²+a²c²d²+b²c²d²;

S₂₂₁₁=a²b²cd+a²bc²d+a²bcd²+ab²c²d+ab²cd²+abc²d².

Mint könnyen ellenőrizhető, az (1) egyenlőtlenség hatodik hatványra emelés és rendezés után a következő:

(2)	2S₃₃+6S₃₂₁+12S₃₁₁₁ $ge$ 15S₂₂₂+24S₂₂₁₁.

A számtani és mértani közép közötti egyenlőtlenség alapján

2S₃₃=(a³b³+a³c³+b³c³)+(a³b³+a³d³+b³d³)+

+(a³c³+a³d³+c³d³)+(b³c³+b³d³+c³d³) $ge$

$ge$ 3a²b²c²+3a²b²d²+3a²c²d²+3b²c²d²=3S₂₂₂.

Hasonlóan kapjuk, hogy S₃₂₁ $ge$ 6S₂₂₂, S₃₂₁ $ge$ 4S₂₂₁₁ valamint 3S₃₁₁₁ $ge$ 2S₂₂₁₁, és így

2S₃₃+6S₃₂₁+12S₃₁₁₁=2S₃₃+2^.S₃₂₁+4^.S₃₂₁+4^.3S₃₁₁₁ $ge$

$ge$ 3S₂₂₂+2^.6S₂₂₂+4^.4S₂₂₁₁+4^.2S₂₂₁₁=15S₂₂₂+24S₂₂₁₁.

2. megoldás. Az f(x)=(x-a)(x-b)(x-c)(x-d) polinomnak négy (nem feltétlenül különböző) pozitív valós gyöke van. Ebből következik, hogy a deriváltjának három pozitív gyöke van; legyenek ezek u, v és w.

A gyökök és együtthatók közötti összefüggések alapján

f'(x)=4x³-3(a+b+c+d)x²+

+2(ab+ac+ad+bc+bd+cd)x-(abc+abd+acd+bcd)=

=4(x³-(u+v+w)x²+(uv+uw+vw)x-uvw).

Tehát

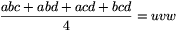
${abc+abd+acd+bcd\over4}=uvw$

és

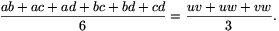
${ab+ac+ad+bc+bd+cd\over6}={uv+uw+vw\over3}.$

A bizonyítandó (1) egyenlőtlenség nem más, mint a számtani és mértani közép közötti egyenlőtlenség az uv, uw és vw számokra.

A. 271. Bizonyítsuk be, hogy tetszőleges p $ge$ 5 prímszámra

(1)	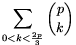$\sum_{0<k<{2p\over3}}{p\choose k}$

osztható p-vel.

Vojtech Jarnik matematikaverseny, Ostrava, 2001

Megoldás. Az (1) összeg minden tagja osztható p-vel. Így azt kell igazolnunk, hogy

(2)	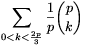$\sum_{0<k<{2p\over3}}{1\over p}{p\choose k}$

osztható p-vel.

Tetszőleges 1 $le$ x<p esetén jelölje x^-1 az x inverzét modulo p, vagyis azt az 1 $le$ y<p számot, amelyre xy $equiv$ 1 (mod p).

Tetszőleges 0<k<p esetén

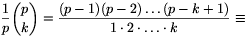
${1\over p}{p\choose k}={(p-1)(p-2)\dots(p-k+1)\over1\cdot2\cdot\dots\cdot k}\equiv$

$equiv$ (-1)^.(-2)^....^.(-k+1)^.1^-1^.2^-1^....^.k^-1 $equiv$ (-1)^k^.k^-1 (mod p),

ezért

$\sum_{0<k<{2p\over3}}{1\over p}{p\choose k}\equiv\sum_{0<k<{2p\over3}}(-1)^k\cdot k^{-1}=$

$=\sum_{0<k<{2p\over3}}k^{-1}-2\sum_{0<k<{p\over3}}(2k)^{-1}\equiv$

$\equiv\sum_{0<k<{2p\over3}}k^{-1}-\sum_{0<k<{p\over3}}{k}^{-1}=\sum_{{p\over3}<k<{2p\over3}}k^{-1}=$

$=\sum_{{p\over3}<k<{p\over2}}(k^{-1}+(p-k)^{-1})\equiv\sum_{{p\over3}<k<{p\over2}}(k+(p-k))\cdot k^{-1}\cdot(p-k)^{-1}=$

$=\sum_{{p\over3}<k<{p\over2}}p\cdot k^{-1}\cdot(p-k)^{-1})\equiv0\pmod p.$

Már regisztráltál?
Új vendég vagy?