 |
A 2001. decemberi informatika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
I. 10. Egy mezőn N darab karót tűztünk ki, ismerjük mindegyik helyét. Szeretnénk bekeríteni azt a területet, amin a karók elhelyezkednek úgy, hogy az N darab karót egy kötéllel kerítjük körbe kívülről (így persze nem mindegyik fog érintkezni a bekerítő kötéllel).
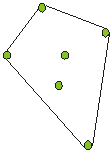
Készíts programot, amely beolvassa N értékét, majd az N karó x- és y-koordinátáját, majd megadja, hogy a területet milyen hosszú kötéllel lehet bekeríteni! (10 pont)
Forrásértelmezés:
Konstans
MaxN=100;
Típus
Pont=Rekord
X,Y:Valós;
Rekord vége
Változók
A kerület kiszámításához kellenek.
sk,kerulet:Valós;
A karók darabszáma.
N,
Ciklusváltozók.
i,j,
A cserénél segédváltozó.
cs,
Index-darabszámok, hány pont van egy-egy részen.
xiya,yaxa,xayi,yixi:Egész;
A karók koordinátái.
adatok:Tömb(1..MaxN:Pont);
Az adatok indexeinek x illetve y szerinti rendezett sorozata.
xsor,ysor,
Ezek tartalmazzák az egyes részekhez tartozó indexeket. Az első és az utolsó a névnek megfelelően, valamilyen szélsőértékű pont.
xmin2ymax,ymax2xmax,
xmax2ymin,ymin2xmin:
Indextömbök
Tömb(1..MaxN: Egész);
rendezés indexelés cseréjével -> xsor, ysor
Be:N; Be:adatok;
xsor és ysor kezdetben az identitás.
Ciklus i:=1-től N-ig
xsor[i]:=i;
ysor[i]:=i;
Ciklus vége;
Majd a rendezés, úgy történik, hogy minden elemmel összehasonlítjuk az összes többit. Persze elég egyszer, ezért a módszerünk - ez a legegyszerűbb rendezési eljárás -, az elsőhöz hasonlítom a másodiktól az utolsóig az összes elemet, majd a másodikhoz a harmadiktól az utolsóig, stb.
Ciklus i:=1-től N-1-ig
Ciklus j:=i+1-től N-ig
Ha adatok.x[xsor[i]]>adatok.x[xsor[j]]
Ha nincs sorrendben, vagyis az előbbre található elem nagyobb, mint a későbbi, akkor cserét kell végrehajtanunk közöttük.
Akkor
cs:=xsor[i];
xsor[i]:=xsor[j];
xsor[j]:=cs;
elágazás vége;
Elvégezve ezt mind az x és y koordinátákra is.
Ha adatok.y[ysor[i]]>adatok.y[ysor[j]]
akkor
cs:=ysor[i];
ysor[i]:=ysor[j];
ysor[j]:=cs;
elágazás vége;
Ciklus vége;
Ciklus vége;
A segédtömbök feltöltése
Ugyanezt a lépést kell négyszer elvégezni, ezért csak itt az elsőnél írom le. Az ötlet az, hogy négy részre osztjuk a kerítési eljárást. Az x és y koordináták szerint sorba rendezés után először az x koordináta szerint minimális ponttól el kell jutnunk az y maximálishoz, majd az x maximálishoz, onnan pedig az y minimálishoz, majd vissza az x minimálishoz. Mindig két szélsőértékű pont között építünk kerítést. Az első esetben az x koordináta szerint minimális ponttól az y szerint maximális ponttig. Így írom le az értelmezést.
i:=1;
Az első pont az x koordináta szerint minimális pont.
xmin2ymax[i]:=xsor[1];
j:=1;
Majd
az összes pontra, az elsőtől az utolsóig, végig kell néznünk, hogy
bele esik-e az éppen vizsgált tartományba, vagyis az elérendő
szélsőértékű pont és az éppen aktuális pont közötti
tartományba. (Aktuális pont alatt azt értjük, hogy az adott részen
addig már húztunk kerítést. Két pont közötti tartományt pedig
bármilyen x érték mellett az y koordinátáknak kell ebbe a tartományba
esni.)
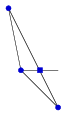
Ha az elérendő szélsőérték (alsó pont) és az éppen aktuális (felső) pont közötti szakasz az ábrán négyzettel jelölt pontjának x koordinátája nagyobb, mint a vizsgált pont koordinátája, akkor ezt is hozzávesszük a kerítést kijelölő karók közé. A négyzettel jelölt pont az a szakaszon az, amelynek y koordinátája megegyezik a vizsgált pont y koordinátájával.
Ciklus amíg j<=N
Ha adatok.y[ysor[j]]>adatok.y[xmin2ymax[i]]
Akkor
Ha adatok.x[xmin2ymax[i]]+
(adatok.x[ysor[N]]-adatok.x[xmin2ymax[i]])*
(adatok.y[ysor[j]]-adatok.y[xmin2ymax[i]])/
(adatok.y[ysor[N]]-adatok.y[xmin2ymax[i]])
>adatok.x[ysor[j]]
akkor
i:=i+1;
xmin2ymax[i]:=ysor[j];
elágazás vége;
elágazás vége;
Majd vesszük a következőt.
j:=j+1;
Ciklus vége;
Lementjük, hogy ebbe a tömbbe hány pontot helyeztünk.
xiya:=i;
Ha az utolsó nem az y maximálisa, akkor azt még el kell mentenünk.
Ha xmin2ymax[xiya]<>ysor[N]
akkor
xiya:=xiya+1;
xmin2ymax[xiya]:=ysor[N];
elágazás vége;
Ugyanígy a többi három részre is a megfelelő átalakításokkal, hiszen a szakaszon levő pontot más pontokból számítjuk és a vizsgált pont, illetve a szakaszon levő pontra is lehet kisebb a feltétel.
i:=1;
ymax2xmax[i]:=ysor[N];
j:=1;
Ciklus amíg j<=N
Ha adatok.x[xsor[j]]>adatok.x[ymax2xmax[i]]
akkor
Ha adatok.x[ymax2xmax[i]]+
(adatok.x[xsor[N]]-adatok.x[ysor[N]])*
(adatok.y[xsor[j]]-adatok.y[ysor[N]])/
(adatok.y[xsor[N]]-adatok.y[ysor[N]])
<adatok.x[xsor[j]]
akkor
i:=i+1;
ymax2xmax[i]:=xsor[j];
elágazás vége;
elágazás vége;
j:=j+1;
ciklus vége;
yaxa:=i;
Ha ymax2xmax[yaxa]<>xsor[N]
akkor
yaxa:=yaxa+1;
ymax2xmax[yaxa]:=xsor[N];
elágazás vége;
i:=1;
xmax2ymin[i]:=xsor[N];
j:=1;
ciklus amíg j<=N
Ha adatok.y[ysor[j]]<adatok.y[xmax2ymin[i]]
akkor
Ha adatok.x[xmax2ymin[i]]+
(adatok.x[ysor[1]]-adatok.x[xmax2ymin[i]])*
(adatok.y[ysor[j]]-adatok.y[xmax2ymin[i]])/
(adatok.y[ysor[1]]-adatok.y[xmax2ymin[i]])
<adatok.x[ysor[j]]
akkor
i:=i+1;
xmax2ymin[i]:=ysor[j];
elágazás vége;
elágazás vége;
j:=j+1;
ciklus vége;
xayi:=i;
Ha xmax2ymin[xayi]<>ysor[1]
akkor
xayi:=xayi+1;
xmax2ymin[xayi]:=ysor[1];
elágazás vége;
i:=1;
ymin2xmin[i]:=ysor[1];
j:=1;
Ciklus amíg j<=N
Ha adatok.x[xsor[j]]<adatok.x[ymin2xmin[i]]
akkor
Ha adatok.x[ymin2xmin[i]]+
(adatok.x[xsor[1]]-adatok.x[ymin2xmin[i]])*
(adatok.y[ysor[j]]-adatok.y[xmin2ymax[i]])/
(adatok.y[xsor[1]]-adatok.y[xmin2ymax[i]])
>adatok.x[ysor[j]]
akkor
i:=i+1;
ymin2xmin[i]:=xsor[j];
elágazás vége;
elágazás vége;
j:=j+1;
ciklus vége;
yixi:=i;
Ha ymin2xmin[yixi]<>xsor[1]
akkor
yixi:=yixi+1;
ymin2xmin[yixi]:=xsor[1];
elágazás vége;
A kerület kiszámítása a segédtömbökből
A kerület kezdetben nulla. ugyanezt a lépést kell négyszer elvégezni, ezért csak itt az elsőnél írom le.
kerulet:=0;
Ha ezen a részen több pont is van, akkor kell kerítés, aminek a hosszát megszámoljuk. Ezt fogjuk hozzáadni az egészet bekerítőhöz.
Ha xiya>1
akkor
i:=2;
sk:=0;
A második indexű elemtől az utolsóig, össze kell számolnunk a szakaszok hosszait (azok összegét).
ciklus amíg i<=xiya
sk:=sk+sqrt((adatok.x[xmin2ymax[i]]-adatok.x[xmin2ymax[i-1]])*
(adatok.x[xmin2ymax[i]]-adatok.x[xmin2ymax[i-1]])+
(adatok.y[xmin2ymax[i]]-adatok.y[xmin2ymax[i-1]])*
(adatok.y[xmin2ymax[i]]-adatok.y[xmin2ymax[i-1]]));
Vagyis a megfelelő, vagyis az összetartozó x illetve y koordinátákból, a \(\displaystyle d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) képlet segítségével számoljuk ki.
Vesszük a következő indexűt.
i:=i+1;
ciklus vége;
A kerület növelése.
kerulet:=kerulet+sk;
elágazás vége;
Ugyanígy a többi részre is.
Ha yaxa>1
akkor
i:=2;
sk:=0;
Ciklus amíg i<=yaxa
sk:=sk+sqrt((adatok.x[ymax2xmax[i]]-adatok.x[ymax2xmax[i-1]])*
(adatok.x[ymax2xmax[i]]-adatok.x[ymax2xmax[i-1]])+
(adatok.y[ymax2xmax[i]]-adatok.y[ymax2xmax[i-1]])*
(adatok.y[ymax2xmax[i]]-adatok.y[ymax2xmax[i-1]]));
i:=i+1;
ciklus vége;
kerulet:=kerulet+sk;
elágazás vége;
Ha xayi>1
akkor
i:=2;
sk:=0;
Ciklus amíg i<=xayi
sk:=sk+sqrt((adatok.x[xmax2ymin[i]]-adatok.x[xmax2ymin[i-1]])*
(adatok.x[xmax2ymin[i]]-adatok.x[xmax2ymin[i-1]])+
(adatok.y[xmax2ymin[i]]-adatok.y[xmax2ymin[i-1]])*
(adatok.y[xmax2ymin[i]]-adatok.y[xmax2ymin[i-1]]));
i:=i+1;
ciklus vége;
kerulet:=kerulet+sk;
elágazás vége;
Ha yixi>1
akkor
i:=2;
sk:=0;
Ciklus amíg i<=yixi
sk:=sk+sqrt((adatok.x[ymin2xmin[i]]-adatok.x[ymin2xmin[i-1]])*
(adatok.x[ymin2xmin[i]]-adatok.x[ymin2xmin[i-1]])+
(adatok.y[ymin2xmin[i]]-adatok.y[ymin2xmin[i-1]])*
(adatok.y[ymin2xmin[i]]-adatok.y[ymin2xmin[i-1]]));
i:=i+1;
ciklus vége;
kerulet:=kerulet+sk;
elágazás vége;
Ki:kerulet;
I. 11. Készíts programot Nap körüli bolygópályák szimulálására! A Nap a képernyő közepén helyezkedjen el, innen nem mozdul, és ismerjük a tömegét (N). A bolygónak ismerjük pillanatnyi helyzetét (X, Y), tömegét (B), valamint sebességét (V), ami a bolygót a Nappal összekötő egyenesre merőleges irányú sebességvektort jelent. Be kell olvasni egy T időközt, amelyben lépésenként számoljuk a bolygó pályáját az eredeti helye, a sebességvektora és a rá ható erők alapján.
Készíts programot, amely beolvassa N, X, Y, B és V értékét, majd rajzolja a bolygópályát! (10 pont)
Forrásértelmezés:
Konstans
Program testek;
Típus
A bolygók síkon levő helyét tárolja majd.
Pont = Rekord(x,y: Valós;);
A bolygók sebesség tárolja ugyancsak a síkon.
Sebesseg = Rekord(vx,vy: Valós;);
Változó
A bolygók gyorsulásának összetevői. Ne tévesszen meg senkit, hogy Pont típusú. Ugyanolyan típusú mezőket tartalmaz a hely, a sebesség és gyorsulás is. A gyorsulásnak már nem hoztunk létre új típust, míg a sebességnek igen.
a1,a2,
A bolygók új koordinátái.
x1,x2,
A bolygók régi koordinátái.
x10,x20 : Pont;
A bolygók új sebessége.
v1,v2,
A bolygók régi sebessége.
v10,v20 : Sebesseg;
A bolygók tömegei.
m1,m2,
A bolygók közt ható erő nagysága.
F,
A bolygók távolságai.
r,
Az időlépés.
t : Valós;
A kirajzolandó grafikus koordinátarendszer középpontjának koordinátái.
sor,oszlop : Egész;
A pálya hiperbola, vagy sem.
hiper : Logikai; Képernyőtörlés;
Tegyük fel, hogy nem hiperbola.
hiper:=HAMIS;
Az adatinicializálás, beolvasás.
x10.x:=0;
x10.y:=0;
v10.vx:=0;
v10.vy:=0;
Be: N;
m1:=N;
Be: X;
x20.x:=X;
Be: Y;
x20.y:=Y;
Be: v20.vx, v20.vy; (V)
Be: B;
m2:=B;
Be: T;
t:=T;
hiper:=(sqr(v20.vx)+sqr(v20.vy))>=
2*m1/sqrt(sqr(x20.x-x10.x)+sqr(x20.y-x10.y));
Akkor hiperbola, ha a kinetikus energiája (amit a sebességéből számítunk) nagyobb, mint a potenciális energia (ami a két test egymásra gyakorolt tömegvonzásából jön)
Grafikus_felület_beállítása; SzínBeállítás(FEHÉR);
Ha hiperbola, akkor nem rajzolunk ki semmit, csak kiírjuk.
Ha hiper
Akkor
SzövegKiíratás(0,0,'hiperbola');
Elágazás vége;
Beállítjuk a koordinátarendszer középpontját.
sor:= MaxY div 2; oszlop:= MaxX div 2;
Kirajzolja a két bolygót.
Kirajzol(x10); Kirajzol(x20);
Billentyűleütésre vár.
KarakterBeolvasás(c);
Addig végzi a szimulációt, amíg nem nyomjuk le az <<Esc>> billentyűt.
Ciklus
r:=sqr(x10.x-x20.x)+sqr(x10.y-x20.y);
A távolság kiszámolása.
Ha még látszik a képernyőn akkor kiszámítjuk a testek közt ható erőt az \(\displaystyle F=k\cdot{m_1\cdot m_2\over r}\) képlet segítségével, k=1 arányossági tényezővel számolva.
Ha r>1
Akkor
F:=m1*m2/r;
A gyorsulást az F=ma képletből kapjuk, persze figyelembe vesszük, hogy koordinátákkal kell számolnunk.
a1.x:=-F/m1*(x10.x-x20.x)/sqrt(r);
a1.y:=-F/m1*(x10.y-x20.y)/sqrt(r);
a2.x:=-F/m2*(x20.x-x10.x)/sqrt(r);
a2.y:=-F/m2*(x20.y-x10.y)/sqrt(r);
A sebesség koordináták kiszámolása az előző sebességekből, illetve a gyorsulásokból lineáris közelítést használva a kis időlépésben.
v1.vx:=v10.vx+a1.x*t;
v1.vy:=v10.vy+a1.y*t;
v2.vx:=v20.vx+a2.x*t;
v2.vy:=v20.vy+a2.y*t;
A hely koordináták kiszámolása az előző koordinátákból, illetve az új sebességekből lineáris közelítést használva a kis időlépésben.
x1.x:=x10.x+v1.vx*t;
x1.y:=x10.y+v1.vy*t;
x2.x:=x20.x+v2.vx*t;
x2.y:=x20.y+v2.vy*t;
A bolygók kirajzolása.
Rajzol(x2,x20);
Lementjük a hely és sebesség koordinátákat.
x10:=x1;
x20:=x2;
v10:=v1;
v20:=v2;
Elágazás vége;
Ha leütöttek egy billentyűt, akkor azt kiolvassa a billentyűzet pufferból.
Ha Billentyű_leütés_történt
akkor KarakterBeolvasás(c);
Elágazás vége;
Amíg c=#27
Ciklus vége;
Grafikus_Felület_Bezárása;
Program vége.
Kis négyzetként jeleníti meg a képernyőn a paraméterként kapott pontot megfelelően eltolva.
Eljárás Kirajzol(x: pont);
rectangle(oszlop+round(x.x-x10.x),sor-round(x.y-x10.y),
oszlop+round(x.x-x10.x)+2,sor-round(x.y-x10.y)+2);
Eljárás vége;
Kirajzolja a Kirajzol eljárás segítségével a paraméterként megkapott két pontot.
Eljárás Rajzol(x,x0: pont);
Kirajzol(x0);
Kirajzol(x);
Eljárás vége;
Pascal program:
|
I. 12. Nagyon sokjegyű (pl. 100) számokat már az Excel sem tud összeadni, illetve szorozni, így más utat kell találni a megvalósításukra. Ha a táblázat egyes celláiba csak egyetlen számjegyet írunk, akkor sokjegyű számok is felírhatók, ezekre azonban el kell készíteni az összeadás és a szorzás műveleteket.
Készíts táblázatot, amely az első két sorba beírt, legfeljebb 100 jegyű számokat (cellánként 1 számjegy) összeadja, illetve szorozza. A szorzat is csak legfeljebb 100 jegyű lehet. A feladat megoldásában a táblázat első 7 sora, illetve 201 oszlopa használható.
Az alábbi példa a megoldás képe legfeljebb 10 jegyű számokra:
|
Megoldás:
Az első oszlop tartalmazza a képen is látható szövegeket. Az első két sor másodiktól számolva 10-10 cellája pedig a két számot. (Ugyanígy megy 100-100-ra is, persze eltolva az egészet.)
Az összeadás az egyszerűbb. Kezdjük azzal. Írjuk az sorba. Segítségül a negyedik sorba is az összeget írjuk, de még nem figyelünk arra, hogy csak egy karaktert írhatunk ki.
A negyedik sor cellájába az összeadást kell írni, úgy hogy figyelünk az előző helyről továbbhozott maradékokra is. [J4]= J1+J2+KEREK.LE(K4/10;0) Tehát a két megfelelő jegyen kívül hozzáadjuk még az előző cellából a maradékot is, amit úgy kapunk, hogy tízzel osztunk, és az egészrészre vagyunk kíváncsiak.
Az ötödik sor egy cellája [J5]=HA(ÉS(I5="";J4=0);"";MARADÉK(J4;10)). Ebben az áll, hogy A negyedik sorban felette álló szám egyesek helyén álló számjegyét írja ki, vagy semmit, attól függően, hogy előtte van-e valami a cellában és a felette levő nulla. Mert ha nincs és nulla, akkor az azt jelenti, hogy a cella még a legnagyobb helyi értékű jegy előtt szerepel.
A szorzás kicsit trükkös:
[M3] = INDEX($B$2:$K$2;2*OSZLOPOK($B$2:$K$2)
- OSZLOPOK($B$2:L$2))
A harmadik sor 12-től 21-ig cellájáig bemásoljuk a második sor 2-től 11-ig cellájáig levő elemeket fordított sorrendben. Vagyis a $B$2:$K$2 tartomány (vektor) elemeit indexeléssel kapjuk meg. Az első helyre az utolsót kell írni, a másodikra az utolsó előttit, stb. Ezt úgy csináljuk, hogy az oszlopok számának kétszereséből kivonjuk az oszlopok számát, majd egyel többet, majd még eggyel többet, stb. $ jel fixálja a sor és oszlop indexeket, így ahol nincs $ ott növekedni fog az oszlopszám, tehát csökken az index. Aminek hatására fordított sorrendben kerülnek kiírásra a tartomány elemei.
[M6] = SZORZATÖSSZEG($B$1:$K$1;D3:M3)
+ KEREK.LE(L6/10;0)
A szorzatösszeg két tartomány (vektor) megfelelő elemeit eleminek szorzatát adja össze. Itt az első sorban levő szám számjegyeit összeszorozzuk a megfordított második szám számjegyeivel és képezzük az összeget. Így elérjük, hogy minden számjegyet minden számjeggyel egyszer összeszorzunk és a helyi értékek is megfelelően alakulnak. Meg még a maradékot adjuk hozzá az előző cellából, amit ismét tízzel történő osztás után kerekítéssel kapunk. A példában a 0000000153 és a 0000000065 vektornak kell a szorzatösszegét venni, ami 45 plusz a (6*3 div 10)=1. Így kapunk 46-ot. 3 db egyes és 5 db tízes, illetve 5 db tízes és 6 db egyes szorzatösszegét képeztük a tízesek helyére.
[M7] = MARADÉK(M6;10)
Itt a felette levő cella egyesek helyén álló számjegyét veszzük. Hiszen a maradékot már figyelembe vettük.
[J7] = HA(ÉS(I7="";INDEX($L$7:$U$7;2*OSZLOPOK($L$7:$U$7)
- OSZLOPOK($L$7:AC$7))=0);"";
INDEX($L$7:$U$7;2*OSZLOPOK($L$7:$U$7)
- OSZLOPOK($L$7:AC$7)))
Ugyanúgy történik, mint [M3]-nál, csak a tartomány megfelelően más (visszafordítjuk), és annyi nehezítéssel, hogy itt is csak akkor írunk ki valamit, ha az már értékes jegy (lásd [J5]-nél).
A megoldás letölthető innen.