KöMaL Problems in Mathematics, September 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2005. |
K. 43. Two students are talking after class. ``What is the average of your computer science marks in September?
-- 4.6 exactly.
-- That is impossible. The school year has just started, you cannot have so many marks yet.''
What may the student in doubt have thought of? (The grades in Hungary are varying from 1 to 5.) (Based on the idea of
(6 pont)
solution (in Hungarian), statistics
K. 44. Determine the acute angles of a right-angled triangle, given that it can be divided into three isosceles triangles as shown in the Figure.
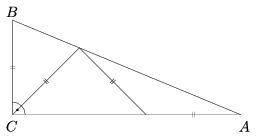
(6 pont)
solution (in Hungarian), statistics
K. 45. In how many different ways is it possible to place a king and a castle on the chessboard so that neither attacks the other? (The fields of the chessboard are labelled by combinations of letters and numbers in the conventional way. Two configurations count as different if at least one of the two chessmen is placed on different fields in the two cases.)
(6 pont)
solution (in Hungarian), statistics
K. 46. The values of a gold artefact in Aurum is proportional to the square of its mass. A 100-dollar piece is stolen by thieves. The thieves cut it up into smaller pieces of equal mass to prepare pendants of them, whose total value is 10 dollars. The pendants are bought up by a jeweller who assembles them into bracelets (of not necessarily the same mass). How much are the individual bracelets worth, given that each bracelet is made of a whole number of pendants, and their total value is 46 dollars?
(6 pont)
solution (in Hungarian), statistics
K. 47. There are two kinds of people living on an island: the good and the bad. The good always tell the truth and the bad always lie. Naturally, every inhabitant of the island is either a boy or a girl. Here is a conversation of two young people on the island:
A: ``If I am good, B is bad.''
B: ``If I am a boy, A is a girl.''
Find out if each of them is good or bad and what sex they belong to.
(6 pont)
solution (in Hungarian), statistics
K. 48. Bob has three stencils for drawing circles. The areas of the circles are 6, 15 and 83 cm2. Bob wants to draw a few circles that have a total area of 220 cm2. How many of each should he draw? (Suggested by D. Szilágyi, Budapest)
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 17, 2005. |
C. 815. The product of the real numbers a and b is 1, and
Find the values of a and b.
(5 pont)
solution (in Hungarian), statistics
C. 816. The price of Aunt Margaret's favourite chocolate has gone up by 30%, while her pension is only raised by 15%. By what percentage will Aunt Margaret's chocolate consumption decrease, if she can only spend 15% more on chocolate.
(5 pont)
solution (in Hungarian), statistics
C. 817. Having calculated that 62+8=44, Clare noticed that 662+88=4444 was also true. Is it true for every n that ?
(5 pont)
solution (in Hungarian), statistics
C. 818. A square tablecloth is layed on a round table so that their centres coincide. The areas of the circle and the square are equal. What percentage of the area of the tabletop is covered by the cloth?
(5 pont)
solution (in Hungarian), statistics
C. 819. A fly is sitting at the centre K of a regular hexagon ABCDEF, there is another fly at vertex B and a spider sitting at vertex A. The flies start clawling from B towards C and from K towards E simultaneously at the same speed. (The spider stays in placed.) Show that the three of them form a regular triangle at every time instant.
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 17, 2005. |
B. 3832. P is an arbitrary point of the hypotenuse AB of a right-angled triangle ABC. The foot of the altitude drawn from vertex C is C1. The projection of P onto the leg AC is A1, and its projection onto the leg BC is B1.
a) Prove that the points P, A1, C, B1, C1 lie on a circle.
b) Prove that the triangles A1B1C1 and ABC are similar.
(3 pont)
B. 3833. Given the points A, B, C and D on the plane, construct a circle passing through A and B, such that the tangents drawn to it from C and D are equal.
(3 pont)
solution (in Hungarian), statistics
B. 3834. What is the largest value of the whole number n, such that with the help of two appropriately chosen weights and an equal-arm balance it is possible to determine the mass of every object that weighs a whole number of kilograms from 1 to n? (It is allowed to carry out as many measurements as needed, only using the two weights and the object to be weighed, and neither the weights nor the objects to be weighted are allowed to be cut in parts.)
(5 pont)
solution (in Hungarian), statistics
B. 3835. This spring there were three Hungarian teams among the best eight in the EHF women's handball championship. When the eight teams were paired randomly, each Hungarian team found that they were playing an opponent from a foreign country. What was the probability of this?
(3 pont)
B. 3836. Represent the values of the number pair p, q on the coordinate plane, such that the equation x2-2px+q=0
a) has two roots;
b) is satisfied by the number 2;
c) is satisfied by the single number 2.
(4 pont)
solution (in Hungarian), statistics
B. 3837. Let P and Q, respectively, denote the centres of the squares ABDE and BCGH drawn on the sides AB and BC of the triangle ABC outwards. The midpoints of the sides AC and DH are R and S, respectively. Show that the points P, Q, R and S are the vertices of a square. (4 points)
(4 pont)
solution (in Hungarian), statistics
B. 3838. The binary form of the positive integer A consists of n digits of 1. Prove that the sum of the digits of the number nA in binary notation is n.
(4 pont)
solution (in Hungarian), statistics
B. 3839. The bisector of the angle A of triangle ABC intersects the side BC at D. The lines b and c drawn through the points B and C, respectively, are parallel to each other and equidistant from A. Let M and N denote the points of the lines b and c, such that AB bisects the line segment DM and AC bisects the line segment DN. Prove that DM=DN.
(5 pont)
solution (in Hungarian), statistics
B. 3840. It is known that the planes of the faces of a tetrahedron divide the space into 15 parts. What is the largest possible number of these parts that a line may pass through?
(4 pont)
solution (in Hungarian), statistics
B. 3841. The problem below appears in the article ``Szalonpóker'' (Hungarian title) of the current issue. Suppose that a deck of 52 cards is suffled in the same way. How many times does it need to be shuffled in order to get back the initial order. Solve the problem for that case, too, when the shuffling starts with the bottom card of the deck on the right, that is, when the card in the 26th place originally is put at the bottom of the new deck.
(Little John and Old Firehand drop in the famous casino of Black Jacky to play cards. They play with a deck of 32 cards numbered 1 to 32. Before they agree on the rules, Black Jacky shuffles the cards as follows: He places the deck on the table, removes the top 16 cards and puts them on the table, to the right of the remaining deck without turning over. Then he forms one deck of them, with the bottom card of the deck on the left lying at the bottom, followed by alternating cards from the two decks. Then he repeats the procedure several times with the deck obtained in this way. Little John is sure that this way of shuffling the cards is not fair. Show that repeating the procedure several times will lead to a surprising result.)
(4 pont)
 |
Problems with sign 'A'Deadline expired on October 17, 2005. |
A. 377. The inscribed circle of the triangle ABC touches the side AB at C1, the side BC at A1, and the side CA at B1. It is known that the line segments AA1, BB1 and CC1 pass through a common point. Let N denote that point. Draw the three circles that pass through N and touches two of the sides. Prove that the six points of tangency are concyclic.
(5 pont)
A. 378. Does there exist a function such that f(x)=-f(y) whenever x and y are different rationals and xy=1 or x+y
 {0,1}?
{0,1}?
(5 pont)
A. 379. Find all real numbers 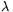 for which there exists a non-zero polynomial P, such that
for which there exists a non-zero polynomial P, such that
for all n. List all such polynomials for 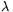 =2.
=2.
(5 pont)
Upload your solutions above.
