A KöMaL 2006. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2006. május 11-én LEJÁRT. |
M. 269. Mérjük meg egy digitális mérőműszer belső ellenállását, ha azt feszültségmérésre állítjuk! Függ-e a belső ellenállás a méréshatártól?
Közli: Varga István, Békéscsaba
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2006. május 11-én LEJÁRT. |
P. 3884. Egy edényben levő víz tetejére olajat rétegeztünk. Az olaj sűrűsége a víz sűrűségének 70%-a. Egy fahasáb úgy úszik az edényben, hogy térfogatának fele a vízbe, negyedrésze pedig az olajba merül. Mennyi a fahasáb anyagának sűrűsége?
Tarján Imre fizikaverseny, Szolnok
(3 pont)
P. 3885. Milyen feltételek teljesülése esetén lehet egyensúlyban az ábrán látható rendszer?
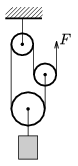
Közli: Gutai László, El Dorado (USA)
(4 pont)
P. 3886. A 2005 végén kirobbant orosz-ukrán árvita idején hazánknak 2,4.109 m3 (normál állapotú) földgáz tartaléka volt. A gáz tárolására Magyarországon is olyan olyan kimerült, vízzel telt szénhidrogén telepeket használnak (pl. Hajdúszoboszlón), ahová mintegy 200 bar nyomással sajtolják be a máshonnan megvett földgázt.
a) Legfeljebb milyen mélyen lehetnek ezek a tárolóhelyek?
b) Legalább mekkora az igénybe vett hazai tárolóhelyek hasznos össztérfogata?
c) A földgáz legnagyobb része metán. Adjunk becslést a besajtolt gáz össztömegére!
d) A földgázt -160 oC alá hűtve és cseppfolyósítva sűrűsége a normál állapotú sűrűség 600-szorosára nő. Hány tartályhajóban férne el a fenti gáztartalék, ha egy tartályhajó befogadóképessége 160 ezer köbméter?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 3887. Vízszintesen, v0=10 m/s sebességgel elhajítunk egy testet. (A közegellenállás elhanyagolható.)
a) Mennyi idő múlva zár be a test sebességvektora az elmozdulásvektorral  =15o-os szöget?
=15o-os szöget?
b) Legfeljebb mekkora szöget zárhat be a sebesség- és az elmozdulásvektor?
Közli: Holics László, Budapest
(5 pont)
P. 3888. Egyenes út A és B pontja között egy ember egyenletes tempóban gyalogol. Az AB szakasz felezőmerőlegesén lévő O pontban egy ember áll, aki dobol. Egy másik alkalommal az A-ból B-be igyekvő, az előzővel azonos sebességű ember dobol, miközben a megfigyelő az O pontban áll. Melyik esetben hall több dobütést a megfigyelő az A és B pont közötti mozgás ideje alatt? (A dobolás mindkét esetben jóval az A-ból történő elindulás előtt kezdődik, és legalább a B-be érkezésig tart. A dobütések időben egyenletesek, periódusidejük a két esetben azonos és sokkal kisebb az A-tól B-ig tartó mozgás idejénél.)
Közli: Pálfalvi László, Pécs
(5 pont)
P. 3889. Vízzel töltött, 20 cm3 térfogatú fecskendő belső keresztmetszete 4 cm2. A fecskendőt függőlegesen felfelé irányítva és a 100 g tömegű dugattyúját állandó sebességgel tolva kinyomjuk belőle a vizet. A víz 1 mm2 keresztmetszetű sugárban 2 m/s sebességgel tör a magasba. (A súrlódási energiaveszteségtől tekintsünk el!)
a) Mekkora sebességgel toljuk a dugattyút?
b) Összesen mennyi munkát végzünk?
c) Határozzuk meg és ábrázoljuk a dugattyúra kifejtett tolóerőt az idő függvényében!
Felvételi feladat nyomán
(4 pont)
P. 3890. Homogén elektrosztatikus mezőbe az erővonalakra merőlegesen egy töltött fémlemezt helyezünk. A fémlemez behelyezése után a lemez bal oldalán E1=5,6.105 V/m, a lemez jobb oldalán pedig E2=3,1.105 V/m az elektromos térerősség nagysága, az irányuk az ábrán látható.
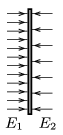
a) Mekkora a fémlemez össztöltése, ha tudjuk, hogy 0,08 N nagyságú elektrosztatikus erő hat rá? (A széleffektusoktól eltekinthetünk.)
b) Mekkora a lemez területe?
Közli: Kotek László, Pécs
(5 pont)
P. 3891. Az ábrán látható hálózat minden ellenállása R. Határozzuk meg a hálózat csomópontjai közti eredő ellenállásokat!
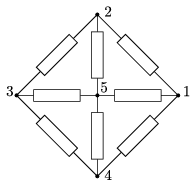
Közli: Cserti József, Budapest
(4 pont)
P. 3892. Egy 5.10-6 m rácsállandójú optikai rácsot a síkjára merőlegesen 680 nm hullámhosszúságú fénnyel világítunk meg.
a) Hány elhajlási maximumot figyelhetünk meg a ráccsal párhuzamosan elhelyezett ernyőn?
b) A beeső fény irányához képest milyen szögben keletkezik a legtávolabbi maximum?
Wigner Jenő fizikaverseny, Békéscsaba
(4 pont)
P. 3893. A hidrogénatomban az elektront rövid ideig helyettesítheti a bomlékony müon. Az így keletkezett atomot müoniumnak nevezik. (A müon az elektronhoz hasonló, de annál 207-szer nagyobb tömegű részecske.) Mekkora a müonium sugara alapállapotban, és mekkora energia kell az ionizálásához?
Adatok: A hidrogénatom sugara kb. 0,05 nm, ionizálási energiája 2,2 aJ.
Szilárd Leó fizikaverseny, Paks
(4 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
|
|

